الطريقة الغوسية – الأردن

ستتعرف في هذه الصفحة على طريقة غاوس-جوردان وكيفية حل نظام من المعادلات باستخدام طريقة غاوس. بالإضافة إلى ذلك، ستجد أيضًا أمثلة وتمارين محلولة للأنظمة باستخدام طريقة غاوس حتى تتمكن من التدرب عليها وفهمها بشكل مثالي.

ما هي طريقة غاوس؟

طريقة غاوس-جوردان هي طريقة تستخدم لحل أنظمة المعادلات ذات 3 مجاهيل، أي كما يلي:

$\left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}$

الهدف من طريقة غاوس هو تحويل نظام المعادلات الأولي إلى نظام متدرج ، أي نظام تكون فيه كل معادلة مجهولة أقل من سابقتها:

$\left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}$

ومع ذلك، للقيام بذلك، عليك أولًا معرفة كيفية التعبير عن نظام من المعادلات في صورة مصفوفة والتحويلات المسموح بها في هذه المصفوفة. لذلك سنشرح هذين الأمرين من قبل، وبعد ذلك سنرى كيفية استخدام إجراء طريقة غاوس .

مصفوفة النظام الموسعة

قبل أن ترى كيف يتم حل النظام، يجب أن تعلم أنه يمكن التعبير عن نظام المعادلات في شكل مصفوفة: معاملات

$x}$

يتم وضعها في العمود الأول، معاملات

$y}$

وفي العمود الثاني معاملات

$z$

في العمود الثالث والأرقام بدون مجهولة في العمود الرابع.

على سبيل المثال:

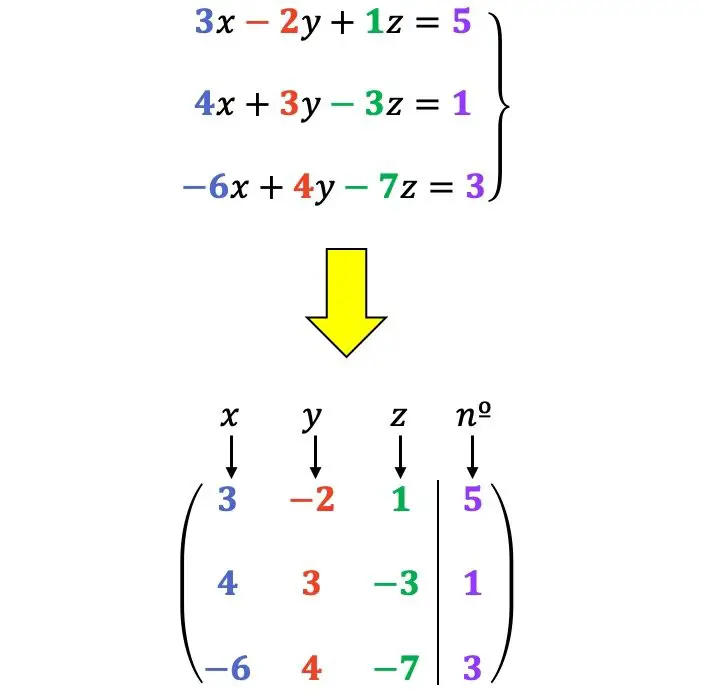
تحويلات الصف المسموح بها

من أجل تحويل نظام المعادلات إلى نظام متدرج، يمكن إجراء إحدى العمليات التالية على المصفوفة المرتبطة بالنظام:

تغيير ترتيب الصفوف في المصفوفة.

على سبيل المثال، يمكننا تغيير ترتيب السطرين 2 و 3 من المصفوفة:

$\left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)$

ضرب أو قسمة جميع الحدود في صف واحد على رقم غير 0.

على سبيل المثال، يمكننا ضرب السطر 1 في 4 وتقسيم السطر 3 على 2:

$\left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)$

استبدل صفًا بمجموع الصف نفسه بالإضافة إلى صف آخر مضروبًا في رقم.

على سبيل المثال، في المصفوفة التالية، نضيف الصف 2 إلى الصف 3 مضروبًا في 1:

$\left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)$

كيفية حل نظام المعادلات باستخدام طريقة غاوس؟

سنرى الآن من خلال مثال طريقة حل نظام المعادلات بطريقة غاوس:

$\left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}$

أول شيء يجب فعله هو المصفوفة الموسعة للنظام :

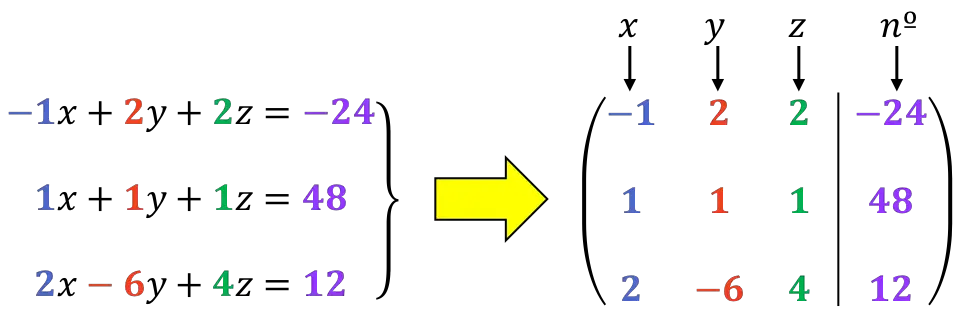
مثال لنظام المعادلات التي تم حلها بطريقة غاوس

وكما سنرى لاحقاً، فمن الأفضل أن يكون الرقم الأول من السطر الأول هو 1. ولذلك سنقوم بتغيير ترتيب السطرين 1 و 2:

$\left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

الهدف من طريقة غاوس هو جعل الأرقام الموجودة أسفل القطر الرئيسي 0 . أي أننا بحاجة إلى تحويل الأرقام الحمراء إلى 0:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)$

لإزالة هذه الأرقام، نحتاج إلى إجراء التحويلات المناسبة للصفوف.

على سبيل المثال، -1، وهو العنصر الأول في الصف الثاني، هو سالب 1، العنصر الأول في الصف الأول. لذلك، إذا أضفنا السطر الأول إلى السطر الثاني، سيتم حذف -1:

$\begin{array}{lccc|c} & -1 & 2 & 2 & -24 \\ + & \phantom{-}1 & 1 & 1 & \phantom{-}48 \\ \hline & \phantom{-}0 & 3 & 3 & \phantom{-}24 \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_2} \\ \color{blue}\bm{\leftarrow f_1} \\ \phantom{hline} \\ \end{array}$

فإذا قمنا بهذا المجموع، فسنحصل على المصفوفة التالية:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

بهذه الطريقة تمكنا من تحويل -1 إلى 0.

الآن سنقوم بتحويل 2. إذا لاحظت، فإن 2، وهو العنصر الأول في الصف الثالث، هو ضعف 1، العنصر الأول في الصف الأول. لذلك، إذا أضفنا الصف الأول مضروبًا في -2 إلى الصف الثالث، فسيتم حذف الـ 2:

$\begin{array}{lccc|c} & \phantom{-}2 & -6 & \phantom{-}4 & \phantom{-}12 \\ + & -2 & -2 & -2 & -96 \\ \hline & \phantom{-}0 & -8 & \phantom{-}2 & -84 \end{array} \begin{array}{l} \color{blue} \bm{\leftarrow f_3} \\ \color{blue} \bm{\leftarrow -2 f_1} \\ \phantom{hline} \\ \end{array}$

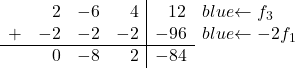
وبذلك ننتهي بالمصفوفة التالية:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)$

وبهذه الطريقة تمكنا من تحويل 2 إلى 0.

كل ما علينا فعله الآن هو تحويل -8 إلى 0. وللقيام بذلك، نضرب السطر الثالث في 3 ونضيف السطر الثاني مضروبًا في 8:

$\begin{array}{lccc|r} & 0 & -24 & \phantom{2}6 & -252 \\ + & 0 & \phantom{-}24 & 24 & \phantom{-}192 \\ \hline & 0 & \phantom{-2}0 & 30 & -60 \end{array} \begin{array}{l}\color{blue}\bm{ \leftarrow 3f_3} \\\color{blue}\bm{ \leftarrow 8f_2} \\ \phantom{hline} \\ \end{array}$

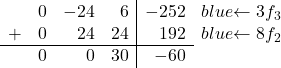
وبالتالي نحصل على المصفوفة التالية:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)$

وبهذه التحويلات، حصلنا على جميع الأرقام الموجودة أسفل القطر الرئيسي لتكون 0. والآن يمكننا حل نظام المعادلات.

يجب علينا الآن تحويل المصفوفة إلى نظام من المعادلات ذات المجهول . للقيام بذلك، تذكر أن العمود الأول يتوافق مع

$x$

، العمود الثاني من

$y$

، العمود الثالث

$z$

والعمود الأخير عبارة عن أرقام بدون مجهولين:

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}$

وأخيرًا، لحل النظام، علينا حل مجاهيل المعادلات من الأسفل إلى الأعلى. بما أن المعادلة الأخيرة لها مجهول واحد فقط، فيمكننا حلها وإيجاد قيمتها:

$30z=-60$

$z = \cfrac{-60}{30}$

$\bm{z=-2}$

الآن بعد أن عرفنا ما هي z، إذا عوضنا بقيمتها في المعادلة الثانية، فيمكننا إيجاد قيمة

$y$

$3y+3z=24 \ \xrightarrow{z \ = \ -2} \ 3y+3(-2)=24$

$3y-6=24$

$3y=24+6$

$3y=30$

$y=\cfrac{30}{3}$

$\bm{y=10}$

ونفعل الشيء نفسه مع المعادلة الأولى: نعوض بقيم المجهولات الأخرى ونمحوها

$x$

$1x+1y+1z=48 \ \xrightarrow{y \ = \ 10 \ ; \ z \ = \ -2} \ 1x+1(10)+1(-2)=48$

$x+10-2=48$

$x=48-10+2$

$\bm{x=40}$

وبالتالي فإن حل نظام المعادلات هو:

$\bm{x=40} \quad \bm{y=10} \quad \bm{z=-2}$

حل مسائل أنظمة المعادلات بطريقة غاوس-جوردان

التمرين 1

حل نظام المعادلات التالي باستخدام طريقة غاوس:

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}$

انظر الحل

أول شيء يتعين علينا القيام به هو المصفوفة الموسعة للنظام:

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)$

الآن نحن بحاجة إلى جعل جميع الأرقام الموجودة أسفل المصفوفة الرئيسية 0.

ولذلك نقوم بإجراء عمليات صفية لإلغاء الحدين الأخيرين من العمود الأول:

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)$

الآن نقوم بإزالة العنصر الأخير من العمود الثاني:

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)$

بمجرد أن تصبح جميع الأرقام الموجودة أسفل القطر الرئيسي 0، يمكننا الآن حل نظام المعادلات. للقيام بذلك، نعبر عن المصفوفة مرة أخرى في شكل نظام من المعادلات ذات المجهول:

$\left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}$

ونحل مجاهيل المعادلات من الأسفل إلى الأعلى. نقوم أولاً بحل المعادلة الأخيرة:

$1z= 1$

$z=\bm{1}$

الآن نعوض بقيمة z في المعادلة الثانية لإيجاد قيمة y:

$-3y+4z=-2 \ \xrightarrow{z \ = \ 1} \ -3y+4(1)=-2$

$-3y+4=-2$

$-3y=-2-4$

$-3y=-6$

$y=\cfrac{-6}{-3} = \bm{2}$

ونفعل الشيء نفسه مع المعادلة الأولى: نعوض بقيم المجهولات الأخرى ونحل لـ x:

$x+y-z=2 \ \xrightarrow{y \ = \ 2 \ ; \ z \ = \ 1} \ x+(2)-(1)=2$

$x+1=2$

$x=2-1$

$\bm{x=1}$

وبالتالي فإن حل نظام المعادلات هو:

$\bm{x=1} \qquad \bm{y=2} \qquad \bm{z=1}$

تمرين 2

أوجد حل نظام المعادلات التالي باستخدام طريقة غاوس:

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}$

انظر الحل

أول شيء يتعين علينا القيام به هو المصفوفة الموسعة للنظام:

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)$

لتطبيق طريقة غاوس، يكون الأمر أبسط إذا كان الرقم الأول في السطر الأول هو 1. لذلك سنقوم بتغيير ترتيب السطرين 1 و 2:

$\left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)$

الآن نحن بحاجة إلى جعل جميع الأرقام الموجودة أسفل المصفوفة الرئيسية 0.

لذلك نقوم بإجراء عمليات الصف لاستبدال العنصرين الأخيرين من العمود الأول:

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)$

نقوم الآن بتحويل العنصر الأخير في العمود الثاني إلى صفر:

$\left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)$

بمجرد أن تكون جميع الأرقام الموجودة أسفل القطر الرئيسي 0، يمكننا حل نظام المعادلات. للقيام بذلك، نعبر عن المصفوفة مرة أخرى في شكل نظام من المعادلات ذات المجهول:

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}$

ونحل مجاهيل المعادلات من الأسفل إلى الأعلى. نقوم أولاً بحل المعادلة الأخيرة:

$-5z= 5$

$z=\cfrac{5}{-5}=\bm{-1}$

الآن نعوض بقيمة z في المعادلة الثانية لإيجاد قيمة y:

$-5y-2z=-13 \ \xrightarrow{z \ = \ -1} \ -5y-2(-1)=-13$

$-5y+2=-13$

$-5y=-13-2$

$-5y=-15$

$y=\cfrac{-15}{-5} = \bm{3}$

ونفعل الشيء نفسه مع المعادلة الأولى: نعوض بقيم المجهولات الأخرى ونحل لـ x:

$x+3y+2z=5 \ \xrightarrow{y \ = \ 3 \ ; \ z \ = \ -1} \ x+3(3)+2(-1)=5$

$x+9-2=5$

$x=5-9+2$

$\bm{x=-2}$

وبالتالي فإن حل نظام المعادلات هو:

$\bm{x=-2} \qquad \bm{y=3} \qquad \bm{z=-1}$

التمرين 3

احسب حل نظام المعادلات التالي بطريقة غاوس:

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}$

انظر الحل

أول شيء يتعين علينا القيام به هو المصفوفة الموسعة للنظام:

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)$

الآن نحن بحاجة إلى جعل جميع الأرقام تحت المصفوفة الأصلية 0.

لذلك نقوم بإجراء عمليات الصف لاستبدال العنصرين الأخيرين من العمود الأول:

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)$

نقوم الآن بتحويل العنصر الأخير في العمود الثاني إلى صفر:

$\left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)$

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}$

ونحل مجاهيل المعادلات من الأسفل إلى الأعلى. نقوم أولاً بحل المعادلة الأخيرة:

$13z= 39$

$z=\cfrac{39}{13}=\bm{3}$

الآن نعوض بقيمة z في المعادلة الثانية لإيجاد قيمة y:

$-5y+z=3 \ \xrightarrow{z \ = \ 3} \ -5y+(3)=3$

$-5y=3-3$

$-5y=0$

$y=\cfrac{0}{-5} = \bm{0}$

ونفعل الشيء نفسه مع المعادلة الأولى: نعوض بقيم المجهولات الأخرى ونحل لـ x:

$2x+3y+1z=-1 \ \xrightarrow{y \ = \ 0 \ ; \ z \ = \ 3} \ 2x+3(0)+1(3)=-1$

$2x+0+3=-1$

$2x=-1-3$

$2x=-4$

$x=\cfrac{-4}{2}=\bm{-2}$

وبالتالي فإن حل نظام المعادلات هو:

$\bm{x=-2} \qquad \bm{y=0} \qquad \bm{z=3}$

التمرين 4

حل نظام المعادلات التالي ذو الثلاثة مجاهيل باستخدام طريقة غاوس:

$\left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}$

انظر الحل

قبل تطبيق طريقة غاوس، نحتاج إلى ترتيب نظام المعادلات بحيث تكون جميع المجهولات على يسار المعادلة والأرقام على اليمين:

$\left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}$

بمجرد ترتيب النظام، نقوم ببناء المصفوفة المطورة للنظام:

$\left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)$

نظرًا لأن جميع الأرقام الموجودة في الصف الأول زوجية، فقبل التعامل مع الصفوف، سنقوم بتقسيم الصف الأول على 2. لأن هذا سيجعل العمليات الحسابية أسهل:

$\left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)$

الآن نحن بحاجة إلى جعل جميع الأرقام الموجودة أسفل المصفوفة الرئيسية 0.

لذلك نقوم بإجراء عمليات الصف لاستبدال العنصرين الأخيرين من العمود الأول:

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)$

كما في السابق، نظرًا لأن جميع الأرقام الموجودة في السطر الأخير هي من مضاعفات الرقم 9، فسوف نقسمها على 9 لتسهيل العمليات الحسابية:

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)$

نقوم الآن بتحويل العنصر الأخير في العمود الثاني إلى صفر:

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}$