طرح كثيرات الحدود

في هذه الصفحة نشرح كيفية طرح كثيرات الحدود. بالإضافة إلى ذلك، ستجد العديد من الأمثلة والتمارين التي تم حلها خطوة بخطوة لطرح كثيرات الحدود.

كيفية طرح كثيرات الحدود؟

لطرح كثيرتي الحدود، يجب عليك طرح حدود كثيرات الحدود المتشابهة. بمعنى آخر، طرح كثيرات الحدود يتكون من طرح الحدود التي لها نفس الجزء الحرفي (نفس المتغيرات ونفس الأسس).

في الرياضيات، يمكنك حساب طرح كثيرات الحدود بطريقتين مختلفتين: الطريقة الرأسية أو الطريقة الأفقية. وفيما يلي شرح لكلا الإجراءين، ولكن ننصحك بتعلم كيفية طرح كثيرات الحدود رأسيًا أولاً ثم الانتقال إلى الطريقة الأفقية. من الواضح أن التمسك بالشخص الذي تفضله.

طرح كثيرات الحدود العمودية

بعد ذلك، سنرى كيف يتم طرح كثيرات الحدود عموديًا باستخدام مثال:

• قم بالطرح

  

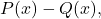
  كونها كثيرة الحدود:

أول شيء يتعين علينا القيام به لإيجاد عملية طرح كثيرة الحدود هو وضع كثيرة الحدود تحت الأخرى، بحيث تتم محاذاة الحدود المتشابهة لكثيرتي الحدود في الأعمدة:

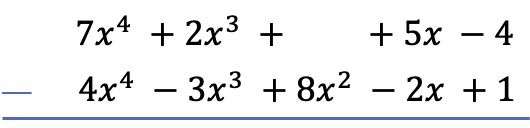
تحذير: إذا لم يكن لدى كثيرة الحدود حد بدرجة معينة، فيجب ترك المساحة فارغة. على سبيل المثال، كثير الحدود

لا تحتوي على وحدة تربيعية أحادية الحد، لذا يوجد مساحة فارغة في مكانها.

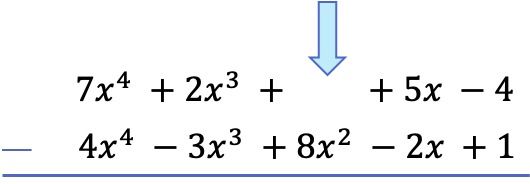
على الرغم من أنه يمكننا الآن طرح كثيرات الحدود مباشرة، إلا أنه من السهل جدًا أن نخطئ في الإشارة إذا فعلنا ذلك بهذه الطريقة. لذلك، لطرح كثيرات الحدود، من الأفضل تغيير إشارة جميع الحدود في كثيرة الحدود الطرحية (كثيرة الحدود الطرحية) ثم إجراء عملية الجمع. بما أن طرح كثيرة الحدود هو نفس إضافة كثيرة الحدود المقابلة لها.

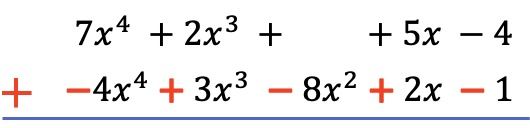
وبمجرد أن قمنا بترتيب جميع الحدود من أعلى درجة إلى أدنى درجة ونفي شروط كثيرة الحدود أدناه، فإننا نضيف معاملات كل عمود مع الحفاظ على الأجزاء الحرفية متساوية:

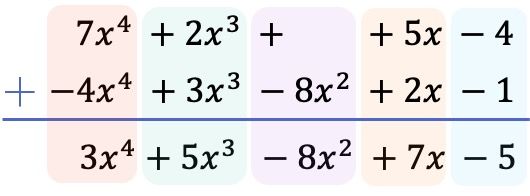
وبالتالي فإن النتيجة التي تم الحصول عليها من طرح كثيرتي الحدود هي:

في حالة عدم وضوح الخطوة الأخيرة بالنسبة لك، أترك لك شرح كيفية جمع كثيرات الحدود ، في الواقع من الضروري أن تتقن جمع كثيرات الحدود لتتمكن من طرح كثيرات الحدود بنجاح. ستجد في الصفحة المرتبطة أيضًا أمثلة وتمارين محلولة لإضافة كثيرات الحدود، وبالإضافة إلى ذلك، ستتمكن من رؤية الاختلافات بين جمع وطرح كثيرات الحدود.

طرح كثيرات الحدود الأفقية

لقد رأينا للتو كيفية طرح كثيرات الحدود رأسيًا، ولكن الآن سنرى الطريقة الأخرى الموجودة لطرح كثيرات الحدود: طرح كثيرات الحدود أفقيًا. من المؤكد أن هذا الإجراء أسرع من الإجراء السابق، إلا أنه من الضروري أن يكون لديك إتقان فائق لمفاهيم كثيرات الحدود.

لذلك دعونا نرى مما تتكون هذه الطريقة لطرح كثيرات الحدود من خلال مثال. وحتى تتمكن من رؤية الاختلافات بين الطريقتين، سوف نقوم بطرح نفس كثيرات الحدود كما في المثال السابق:

• احسب الباقي

  

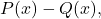
  كونها كثيرة الحدود:

يجب علينا أولاً أن نضع كثيرتي الحدود في صورة عملية جبرية، أي واحدة تلو الأخرى:

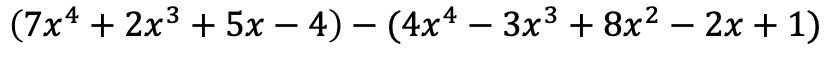
تظل وحيدات الحد الموجودة في القوس الأول كما هي، ولكن يجب أن تتغير الإشارة الموجودة في القوس الثاني لأن لها علامة سالبة في المقدمة:

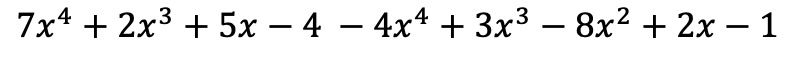
والآن نقوم بتجميع الحدود التي تحتوي على أجزاء حرفية متطابقة، أي الحدود التي لها نفس المتغيرات (الحروف) والأسس. المصطلحات غير المتشابهة لا يمكن إضافتها أو طرحها.

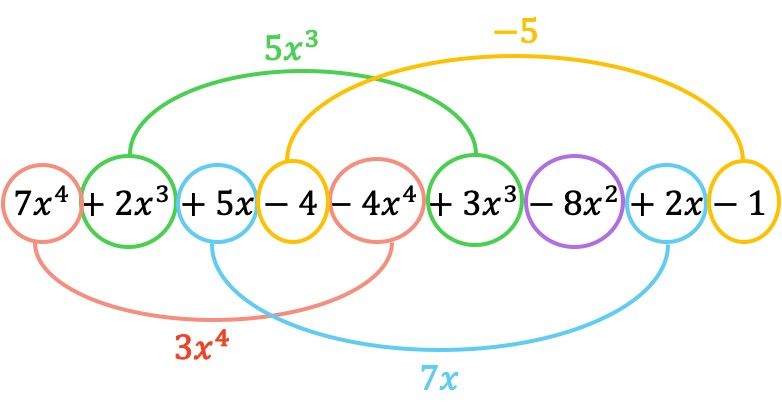
وبالتالي فإن كثيرة الحدود الناتجة عن الطرح هي:

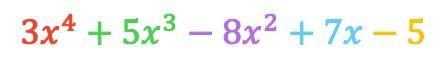
كما ترون، حصلنا على نفس النتيجة في كلتا الطريقتين، لذا يمكنك استخدام أيهما يناسبك.

الآن بعد أن رأيت الطريقتين لحل طرح كثيرات الحدود، هل تعلم أنه يمكنك أيضًا طرح الكسور ذات كثيرات الحدود؟ وليس فقط عمليات الطرح، ولكن جميع أنواع العمليات. تعرف على كيفية إجراء العمليات على الكسور الجبرية بالضغط على هذا الرابط.

حل مسائل طرح كثيرات الحدود

لكي تتمكن من التدرب، نتركك مع العديد من تمارين طرح كثيرات الحدود التي تم حلها. إذا كانت لديكم أسئلة حول أحد التمارين يمكنكم طرحها في التعليقات على الصفحة، وسنقوم بالرد عليها في أقرب وقت ممكن.

التمرين 1

اطرح كثيرة الحدود

ناقص كثير الحدود

في هذه الحالة، سنطرح كثيرتي الحدود رأسيًا. للقيام بذلك، نرتب أولًا كثيرات الحدود حسب الدرجة، ثم نغير إشارة حدود كثيرات الحدود المتبقية، وأخيرًا، نضيف أحاديات الحد الموجودة في نفس العمود:

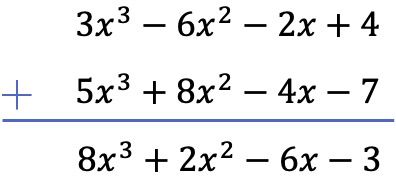
تمرين 2

حل كثيرة الحدود الطرح

ناقص كثير الحدود

إن طرح كثيرتي الحدود يعادل إضافة عكس كثير الحدود المطروحة إلى كثير الحدود المصغر. ولذلك نغير إشارة شروط كثيرة حدود المقاولة من الباطن (الباقية) ونضيف كثيرات الحدود:

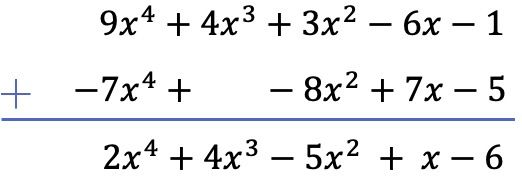
لاحظ أنه في هذه الحالة بالذات يجب ترك مساحة فارغة في عمود الدرجة 3 من كثيرة الحدود الثانية، حيث لا يوجد بها حد من الدرجة الثالثة.

التمرين 3

أوجد نتيجة طرح كثيرة الحدود

ناقص كثير الحدود

في هذه الحالة، سنحل عملية طرح كثيرتي الحدود رأسيًا. لذلك، نقوم أولاً بترتيب كثيرات الحدود من الأكبر إلى الأصغر درجة، ثم نغير إشارة حدود كثيرة الحدود المتبقية، وأخيرًا نضيف الحدود المتشابهة:

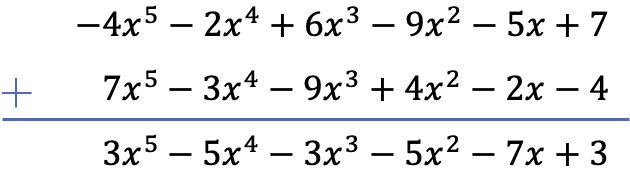
التمرين 4

احسب العملية التالية مع كثيرات الحدود:

في هذه الحالة، هناك 3 كثيرات حدود متضمنة في العملية، 2 منها عبارة عن عمليات طرح. ولذلك، لحل العملية، سنغير إشارة جميع حدود كثيرتي الحدود المتبقيتين، ثم سنضيف كثيرات الحدود.

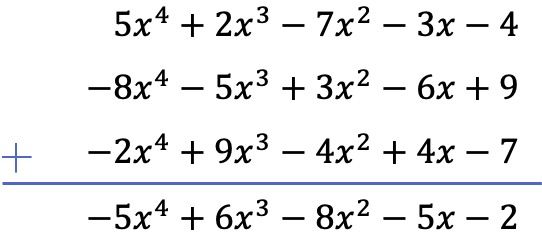
ما رأيك في التفسير؟ هل وجدت أنه من المفيد؟ ما هي طريقة طرح كثيرات الحدود التي تفضلها، رأسيًا أم أفقيًا؟ نقرأ لك في التعليقات! 👀