الأعداد المركبة هي مجموعة مكونة من أعداد حقيقية وأعداد خيالية . يمكن تمثيل هاتين المجموعتين العدديتين الأخيرتين بيانياً باستخدام الخط الحقيقي والخط التخيلي. وعندما نضع كلا الخطين في المستوى نفسه، يتشكل المستوى المركب المعروف.
ما هي الخطة المعقدة؟
يتكون المستوى المركب من المحور الحقيقي (المحور X)، وهو ما يعادل الخط الحقيقي، ومن ناحية أخرى، المحور التخيلي (المحور Y)، الذي يصور الخط التخيلي.
وتجدر الإشارة إلى أن هذه الخطة تشمل جميع الأعداد المركبة. ولذلك، مهما كان العدد المركب صغيرا أو صغيرا، أو الشكل الذي كتب به العدد المركب، فإنه يمكن تمثيله بيانيا على المخطط. لذلك دعونا نرى كيف يتم تمثيل هذه الأرقام في المستوى المركب.
كيفية رسم الأعداد المركبة على المستوى المركب؟
كما نعلم بالفعل (أو إذا كنت لا تعرف، ننصحك بقراءة مقالتنا عنالأعداد المركبة )، هناك ثلاث طرق لكتابة مركب: الصورة ذات الحدين، والصورة القطبية، والصورة المثلثية. يعبر كل منها عن القيمة المعقدة وفقًا لبنية مختلفة، وبالتالي فإن الطريقة التي يجب اتباعها لعمل التمثيلات الرسومية مختلفة.
وبعد ذلك نوضح الإجراء الواجب اتباعه في الحالات الثلاث:
التمثيل في شكل ذي الحدين
عندما يكون لدينا رقم مركب بالترميز ذي الحدين ، وهو الأكثر شيوعًا، يجب أن ننظر إلى بنية الرقم:

حيث a هو الجزء الحقيقي و b هو الجزء التخيلي.
بمعرفة ذلك، نستنتج أن قيمة a هي التي نستخدمها للإحداثي الإحداثي (المحور الحقيقي) وقيمة b هي التي نستخدمها للكمبيوتر (المحور التخيلي). مع المثال التالي سوف تفهم ذلك بشكل أفضل.
سنحاول تمثيل الرقم: 3 + 2i.
أول شيء هو رسم الرسم البياني (مع ملاحظة أن المحور الأفقي هو المحور الحقيقي والمحور الرأسي هو المحور التخيلي):

ثم نقوم بتحديد نقطة الرسم البياني بالإحداثيات الديكارتية (x، y)، والتي نستنتجها من العدد المركب. في هذا المثال العملي، نقطتنا هي (3، 2).
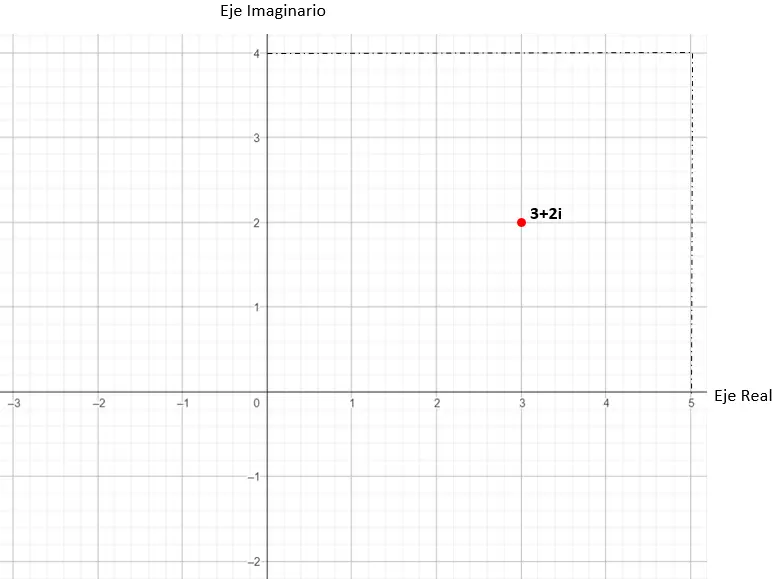
وبالتالي سيتم تمثيل القيمة 3 + 2i في المستوى المركب.
التمثيل في الشكل القطبي
سنرى الآن كيف يتم تمثيل العدد المركب على الصورة القطبية . لفهم هذه الطريقة بشكل كامل، عليك أن تعرف أن التدوين القطبي يحدد عددًا مركبًا بناءً على الوحدة والوسيطة. والتي تستخدم في التمثيل البياني كإحداثيات قطبية (وليس كإحداثيات ديكارتية!).
والسمة الرئيسية لنظام الإحداثيات القطبية هي أن موقع النقطة يتم وصفه عن طريق متجه وزاوية (ليس مثل الطريقة السابقة). الذي يتوافق مع الوحدة النمطية ووسيطة الأعداد المركبة. بعد ذلك، نعرض لك الصيغة الشاملة للصيغة القطبية للعدد المركب:

حيث |ض| هو المعامل و α هي الوسيطة. ويتم ترجمة هذين المتغيرين في الخطة من خلال:
- الوحدة النمطية: هي الطول الذي يحدد المتجه (بين الأصل والنقطة المكافئة للرقم الذي لدينا).
- الوسيطة: هي الزاوية التي يصنعها المتجه مع المحور X.
ومن ثم، فإن مقياس العدد المركب يتوافق مع طول المتجه الذي نستخدمه لرسم الرسم البياني. في حين أن وسيطة أو زاوية العدد المركب هي الزاوية بين المتجه والمحور X. أدناه يمكنك رؤية رسم تخطيطي يضع جميع المتغيرات :
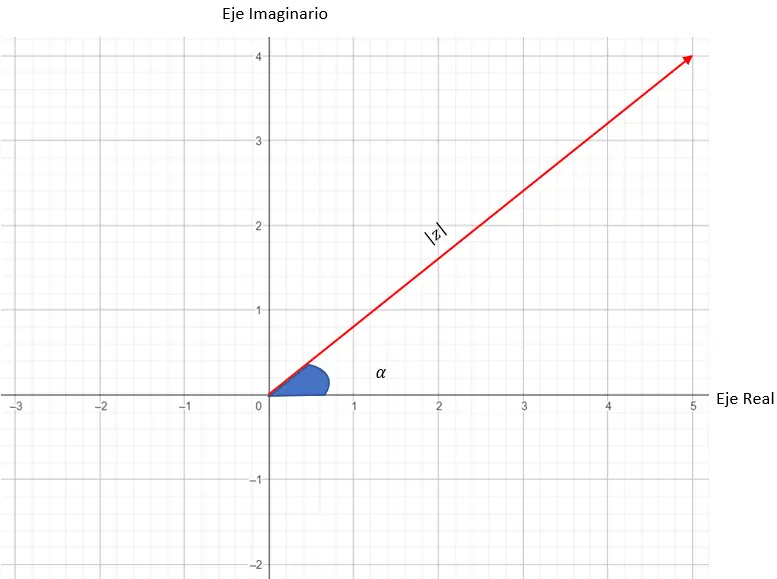
الآن سنحاول تمثيل الرقم: 3 45 .
أولاً، نحتاج إلى تحديد الوحدة والوسيطة:
- الوحدة: 3.
- الحجة: 45 درجة.
بعد ذلك نحتاج إلى العثور على النقاط على الرسم البياني التي معاملها يساوي 3، وفي هذه الحالة أي نقطة على دائرة نصف قطرها 3 ستعمل.
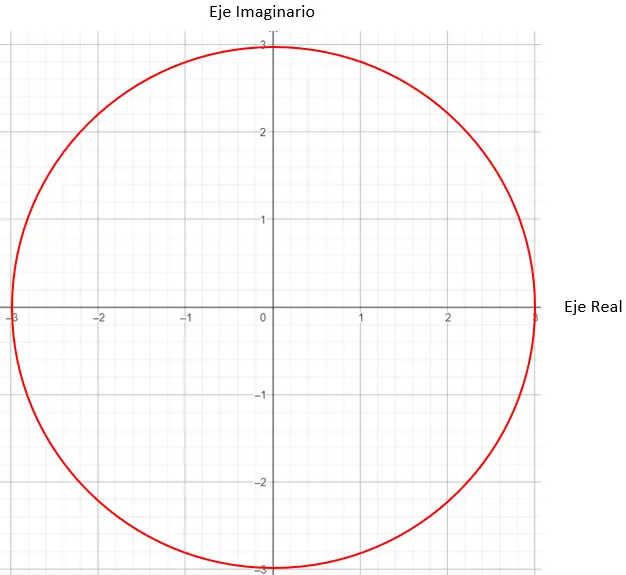
وللانتهاء من تحديد النقطة الدقيقة، يجب أن نضع شرطًا وهو أن المتجه الناتج عن الوحدة ونقطة الأصل يجب أن يصنع زاوية قدرها 45 درجة مع المحور X.
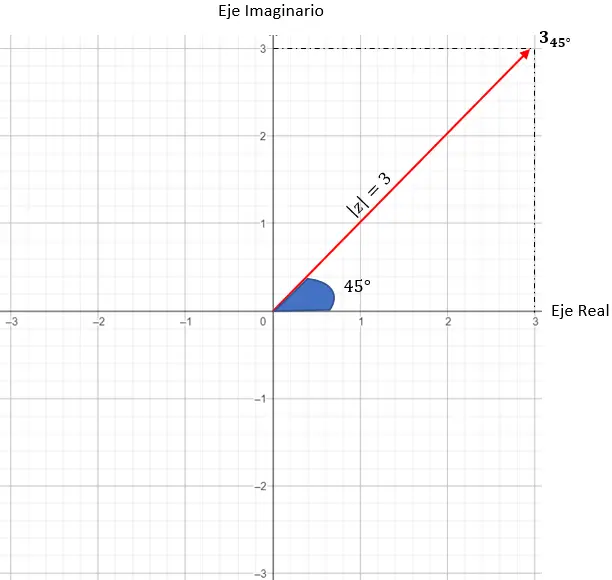
ولدينا بالفعل عدد مركب ممثل بالرمز القطبي.
التمثيل في شكل مثلثي
أخيرًا، لا يزال يتعين علينا شرح كيفية تمثيل العدد المركب في الصورة المثلثية . هذه الحالة والحالة السابقة متماثلتان عمليًا، لأن الشكل القطبي والشكل المثلثي يستخدمان نفس البيانات للتعبير عن رقم مركب: المعامل والوسيطة. هذا يغير فقط بنية التعبير:

أين، |z| هو المعامل و α هي الوسيطة.
لذلك يجب علينا الاستفادة من نفس الطريقة كما في الحالة السابقة: استخدام الوحدة باعتبارها “الطول” والوسيطة باعتبارها زاوية. ومن خلال رؤية المثال التالي، سوف تفهمه بشكل أفضل.
سنمثل z = 4 · (cos (45) + i · sin(45)).
أول شيء هو تحديد الوحدة والزاوية:
- الوحدة: 4.
- الحجة: 45 درجة.
بعد ذلك، نحتاج إلى العثور على النقاط على الرسم البياني التي لها معامل يساوي 4، وفي هذه الحالة أي نقطة على دائرة نصف قطرها 4 ستعمل.
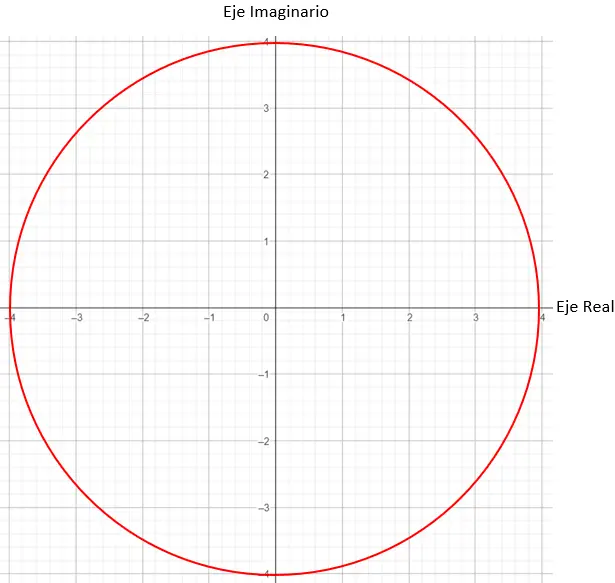
وأخيرًا، حددنا النقطة الدقيقة، مما يتطلب أن تكون الزاوية المتكونة بين متجه المعامل والمحور X 45 درجة، كما تخبرنا الحجة.
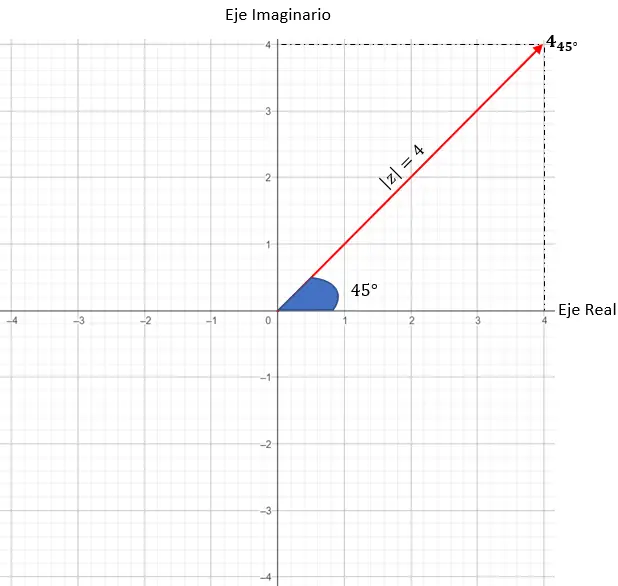
ومن ثم، فإننا نمثل عددًا مركبًا على الصورة المثلثية.
تمرين الطائرة المعقدة
لإنهاء هذا المنشور، سنقدم تمرينًا أخيرًا. نوصي بشدة بحلها، لأنه بهذه الطريقة ستدمج المعرفة الموضحة خلال هذه المقالة.
إثبات التمثيل البياني للأعداد المركبة الثلاثة التالية على المستوى المركب:
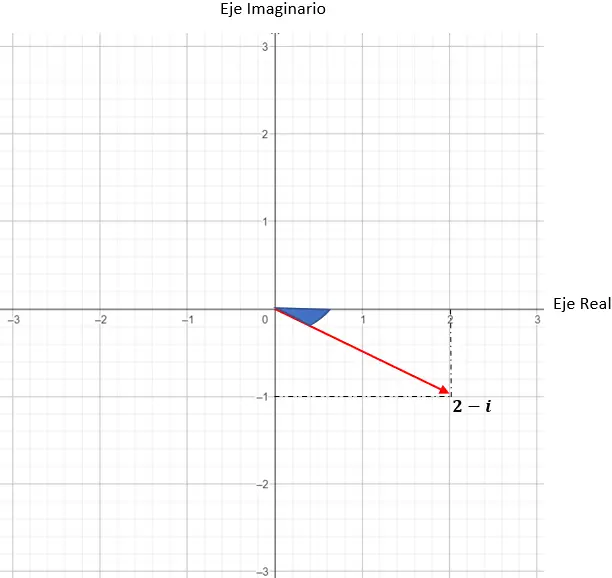
ض = 2 – ط
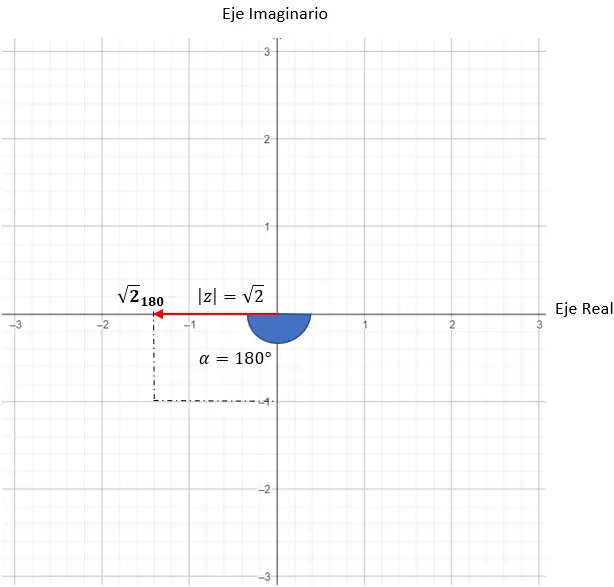
ث = √2180
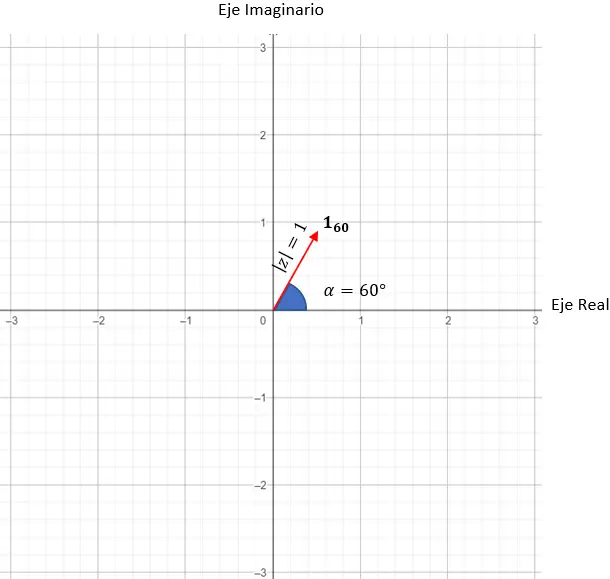
ع = جتا (60) + خطيئة (60)
تعرف على المزيد حول الخطة المعقدة
- ارقام مركبة
- أرقام خيالية