الطائرات الموازية

ستجد في هذه الصفحة كل ما يتعلق بالمستويين المتوازيين: عندما يكون مستويان متوازيين، معادلات المستويين المتوازيين، أمثلة، تمارين محلولة، خصائص،…

ما هما الطائرتان المتوازيتان؟

في الهندسة التحليلية، يكون المستويان متوازيين عندما تكون المسافة بينهما دائمًا متساوية. ولذلك، فإن المستويين المتوازيين لا يتقاطعان أبدًا وليس بينهما أي شيء مشترك.

إن وضع مستويين متوازيين ليس هو الموضع النسبي الوحيد الممكن بين المستويات، حيث أن المستويين في الفضاء (في R3) يمكن أن يكونا متقاطعين أو متطابقين أيضًا.

كيف يمكنك معرفة ما إذا كانت طائرتان متوازيتان؟

بعد الاطلاع على تعريف المستويين المتوازيين، دعونا نرى كيف يمكنك تحديد ما إذا كان المستويان متوازيين أم لا.

بدءاً من المعادلة العامة (أو الضمنية) لخطتين مختلفتين:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1 =0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2 =0$

سيكون المستويان متوازيين إذا كانت معاملاتهما A وB وC متناسبة مع بعضها البعض وليس مع المعامل D. وبعبارة أخرى، يحدث التوازي بين المستويين عندما تتحقق المعادلة التالية:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white ]}]{equation*} \cfrac{A_1}{A_2}=\cfrac{B_1}{B_2} = \cfrac{C_1}{C_2}\neq \cfrac{D_1}{D_2} \end{empheq}$

مثال على طائرتين متوازيتين

على سبيل المثال، المستويان التاليان متوازيان:

$\pi_1 : \ 6x+2y-4z+1 =0$

$\pi_2 : \ 3x+y-2z+5 =0$

المخططات متوازية لأن معاملات المتغيرات X، Y، Z تتناسب مع بعضها البعض، ولكن ليس مع الحدود المستقلة:

$\cfrac{6}{3} =\cfrac{2}{1} =\cfrac{-4}{-2} \neq \cfrac{1}{5} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

حساب المسافة بين طائرتين متوازيتين

المستويان المتوازيان يقعان دائمًا على نفس المسافة، لذلك لإيجاد المسافة بين مستويين متوازيين، يمكننا أخذ نقطة على أحد المستويين وحساب المسافة من تلك النقطة إلى المستوى الآخر. لذلك، لحساب المسافة بين مستويين متوازيين، من الضروري معرفة صيغة المسافة من نقطة إلى مستوى .

إنها طريقة لإيجاد المسافة بين طائرتين متوازيتين. ومع ذلك، هناك طريقة أبسط للقيام بذلك عندما تتطابق المعاملات A وB وC لمعادلات المستويين:

خذ بعين الاعتبار المعادلات العامة (أو الضمنية) لمستويين متوازيين:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

صيغة حساب المسافة بين مستويين متوازيين هي:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

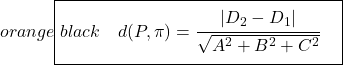
لذا فمن المؤكد أنه من الأسهل العثور على المسافة بين مستويين متوازيين باستخدام الصيغة، لأنها مجرد مسألة تطبيق الصيغة وهذا كل شيء، لكن ذلك يعتمد على المشكلة. بالإضافة إلى ذلك، نعتقد أنه من الأفضل شرح كلتا الطريقتين لحساب المسافة حتى تتمكن من اختيار الطريقة التي تفضلها.

مثال لحساب المسافة بين طائرتين متوازيتين

على سبيل المثال، سوف نحسب المسافة بين المستويين التاليين:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

يجب علينا أولًا أن نتحقق من أننا نتعامل مع طائرتين متوازيتين. وبالتالي، فإن جميع معاملات المعادلات المستوية متناسبة باستثناء الحدود المستقلة، لذا فهما مستويان متوازيان فعليًا.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

وفي هذه الحالة لا تتطابق مصطلحات A وB وC لمعادلات المستويين، لكن يمكننا تحقيق ذلك بقسمة معادلة المستوى الثاني بأكملها على اثنين:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

لذا، أصبحت معادلات المستويين الآن لها نفس المعاملات A وB وC. لذلك، يمكننا بسهولة حساب المسافة بين المستويين باستخدام صيغة المسافة بين مستويين متوازيين:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

نستبدل القيم ونحل العمليات:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

بحيث تكون المسافة بين أحد المستويين والمستوى الآخر تساوي الوحدة.

خصائص الطائرات المتوازية

خصائص الطائرات المتوازية هي كما يلي:

الخاصية الانعكاسية : كل مستوى موازي لنفسه.

$\pi_1 \parallel \pi_1$

خاصية التناظر : إذا كان أحد المستويين موازيا للآخر، فإن هذا المستوي موازي للأول أيضا. هذه الخاصية تمتلكها أيضًا الطائرات المتعامدة.

$\pi_1 \parallel \pi_2 \ \longrightarrow \ \pi_2 \parallel \pi_1$

خاصية متعدية : إذا كان المستوى موازيا لمستوى آخر، وهذا المستوى الثاني موازي لمستوى ثالث، فإن المستوى الأول موازي للمستوى الثالث أيضا.

$\left. \begin{array}{c} \pi_1 \parallel \pi_2\\[2ex] \pi_2 \parallel \pi_3 \end{array} \right\} \longrightarrow \ \pi_1 \parallel \pi_3$

طائرات متوازية