الطائرات المتعامدة

ستجد في هذه الصفحة ما هي المستويات المتعامدة، وكيفية تحديد ما إذا كان هناك مستويان متعامدان، وكيفية حساب المستوى المتعامد، وأمثلة وتمارين محلولة للمستويات المتعامدة،…

ما هما الطائرتان المتعامدتان؟

في الهندسة التحليلية، يكون المستويان متعامدين عندما يتقاطعان بزاوية قائمة (90 درجة).

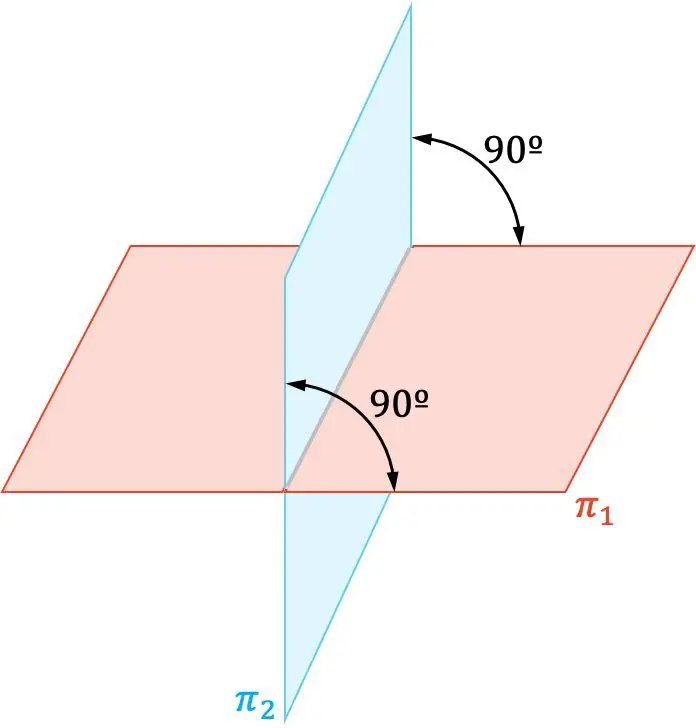
علاوة على ذلك، فإن المتجهات العادية لمستويين متعامدين تكون أيضًا متعامدة مع بعضها البعض.

ومن الواضح أن المسافة بين مستويين متعامدين تكون دائمًا صفرًا، لأنهما يتقاطعان في خط مستقيم. على الرغم من أن الأمر يبدو بسيطًا جدًا، إلا أن مفهوم المسافة بين طائرتين مهم جدًا، لذا ننصحك بزيارة الرابط إذا كان لديك أي أسئلة حول هذا الموضوع.

من ناحية أخرى، فإن وضع مستويين بشكل متعامد ليس هو الموقع النسبي الوحيد الممكن بين المستويات، حيث أن المستويين في الفضاء (في R3) يمكن أيضًا أن يكونا متقاطعين أو متوازيين أو متطابقين.

كيف يمكنك معرفة ما إذا كان أحد المستويين متعامدًا مع الآخر؟

بعد أن رأينا تعريف المستويات المتعامدة، دعونا نرى كيفية معرفة ما إذا كان المستويان متعامدين أم لا:

تكون المستويتان متعامدتين عندما تكون متجهاتهما الطبيعية متعامدة. لذلك، لتحديد ما إذا كان المستويان متعامدين مع بعضهما البعض، يجب علينا حساب الزاوية التي تشكلها ناقلاتهما العادية، وإذا كانت هذه تشكل زاوية 90 درجة، فهذا يعني أن المستويين متعامدان.

لذلك، للعثور على عمودي طائرتين، عليك أن تعرف كيفية حساب الزاوية بين متجهين . إذا كنت لا تتذكر كيفية القيام بذلك، يمكنك الرجوع إلى الرابط، حيث ستجد شرحنا بالإضافة إلى الصيغة اللازمة لتحديد الزاوية بين متجهين. بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتدرب على التمارين التي تم حلها.

لكن باختصار، يكون المتجهان متعامدين عندما يكون حاصل الضرب القياسي لهما صفرًا. لذلك، سيكون المستويان متعامدين عندما يكون حاصل الضرب النقطي للمتجهات العادية المرتبطة بهما 0.

مثال على طائرتين متعامدتين

على سبيل المثال، دعونا نتحقق مما إذا كان المستويان التاليان متعامدين:

$\pi_1 : \ 3x-4y+2z+5 =0$

$\pi_2 : \ 2x+5y+7z-6 =0$

تتطابق إحداثيات X وY وZ للمتجه الطبيعي للمستوى مع المعاملات A وB وC لمعادلته العامة (أو الضمنية). وبالتالي فإن المتجه الطبيعي لكل مستوى هو:

$\vv{n}_1 =(3,-4,2)$

$\vv{n}_2 =(2,5,7)$

والآن نتحقق مما إذا كانت هاتان المستويتان متعامدتان عن طريق حساب حاصل الضرب النقطي بين متجهيهما العاديين:

$\begin{aligned} \vv{n}_1 \cdot \vv{n}_2 & = (3,-4,2)\cdot (2,5,7) \\[2ex] & = 3 \cdot 2 +(-4) \cdot 5 +2 \cdot 7 \\[2ex] &=6-20+14 \\[2ex] &\bm{= 0}\end{aligned}$

حاصل الضرب النقطي بين المتجهين الطبيعيين هو 0، لذا فإن المستويين متعامدان مع بعضهما البعض.

حساب مستوى عمودي على خط عند نقطة ما

مشكلة المستويات والخطوط النموذجية هي إيجاد معادلة المستوى العمودي على خط عند نقطة معينة. لذلك، بعد ذلك سنرى كيف يتم حلها عن طريق مثال:

أوجد معادلة المستوى العمودي على الخط.
$r$

عن

$P,$

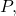
يقال مباشرة ونقطة:

$\displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=-1+4t \\[1.7ex] z=1+t \end{cases} \qquad \qquad P(1,3,-2)$

أولًا، علينا إيجاد المتجه العمودي للمستوى المعني. ومثل الخط المستقيم

$r$

عموديًا على المستوى، فإن متجهه الطبيعي سيتزامن مع متجه الاتجاه للخط.

في هذه الحالة الخط

$r$

يكون على شكل معادلات بارامترية، وبالتالي فإن مكونات متجه اتجاهه هي الحدود الموجودة أمام المعلمة

$t:$

$\vv{r} =(-2,4,1)$

وبالتالي، فإن المتجه العمودي للمستوى سيكون هو نفسه متجه الاتجاه للخط:

$\vv{n} =(-2,4,1)$

وبالتالي فإن المعادلة الضمنية (أو العامة) للخطة ستكون كما يلي:

$\pi : \ -2x+4y+1z+D=0$

لذلك يكفي تحديد قيمة المعامل D. وللقيام بذلك، نعوض في معادلتها بإحداثيات النقطة التي تخبرنا بيانها أنها تنتمي إلى المستوى:

$P(1,3,-2)$

$-2\cdot 1+4\cdot 3-2+D=0$

$-2+12-2+D=0$

$8+D=0$

$D=-8$

وباختصار فإن المعادلة الديكارتية للمستوى هي:

$\bm{\pi : \ -2x+4y+z-8=0}$

من ناحية أخرى، إذا كنت ترغب في ممارسة المزيد من التمارين على العمودي بين الكائنات الهندسية، يمكنك زيارة صفحتنا حول الخطوط المتعامدة. ستجد كل ما تحتاج لمعرفته حول الخطوط المتعامدة : عندما يكون خطان متعامدين، وكيفية حساب خط متعامد على الآخر، وأمثلة، وتمارين محلولة، وغير ذلك الكثير.

خصائص الطائرات المتعامدة

تتميز جميع المستويات المتعامدة بالخصائص التالية:

العلاقة التناظرية : إذا كان المستوى عموديًا على مستوى آخر، فإن هذا المستوى يكون أيضًا عموديًا على المستوى الأول. يتم الاحتفاظ بهذه الخاصية أيضًا بواسطة طائرات متوازية.

$\pi_1 \bm{\perp} \pi_2 \ \longrightarrow \ \pi_2 \bm{\perp} \pi_1$

الخاصية غير الانعكاسية : من الواضح أنه لا يمكن لأي مستوى أن يكون عموديا على نفسه.

$\pi_1 \ \cancel{\bm{\perp}}} \ \pi_1$

النظرية: في الفضاء ثلاثي الأبعاد، أي زوج من المستويات المتعامدة مع مستوى ثالث يجب بالضرورة أن يكون متوازيًا. بمعنى آخر، إذا كان المستوى متعامدًا مع مستوى آخر وكان هذا المستوى أيضًا متعامدًا مع مستوى ثالث، فإن المستويين الأول والأخير يكونان متوازيين مع بعضهما البعض.

طائرات عمودية

ما هما الطائرتان المتعامدتان؟

كيف يمكنك معرفة ما إذا كان أحد المستويين متعامدًا مع الآخر؟

مثال على طائرتين متعامدتين

حساب مستوى عمودي على خط عند نقطة ما

خصائص الطائرات المتعامدة

اترك تعليقاً إلغاء الرد