▷ كيفية ضرب كثيرات الحدود (تمارين محلولة)

في هذه الصفحة سوف تتعلم كيفية ضرب كثيرات الحدود. ستتمكن أيضًا من رؤية أمثلة على ضرب كثيرات الحدود، بالإضافة إلى حل التمارين خطوة بخطوة. وأخيرا، سوف تكتشف ما هي خصائص ضرب كثيرات الحدود.

ومع ذلك، لفهم مفهوم ضرب كثيرات الحدود بشكل كامل، سننتقل من الأكثر أساسية إلى الأكثر تعقيدًا، أي أننا سنبدأ بكيفية ضرب كثيرات الحدود في عدد، وبعد ذلك سنرى كيفية ضرب كثيرات الحدود في عدد أحادية الحد، وأخيرًا، سنشرح كيفية ضرب متعددتي الحدود أو أكثر معًا.

أنصحك باتباع هذا الترتيب، ولكن إذا كنت تعتقد أنك قد أتقنت بالفعل العمليات مع كثيرات الحدود السابقة، فيمكنك الانتقال مباشرة إلى الضرب بين كثيرات الحدود من خلال النقر على الفهرس:

ضرب كثير الحدود برقم

من السهل جدًا حل حاصل ضرب عددية (أو رقم) وكثيرة الحدود، فقط قم بضرب الرقم في معامل كل حد من كثيرة الحدود .

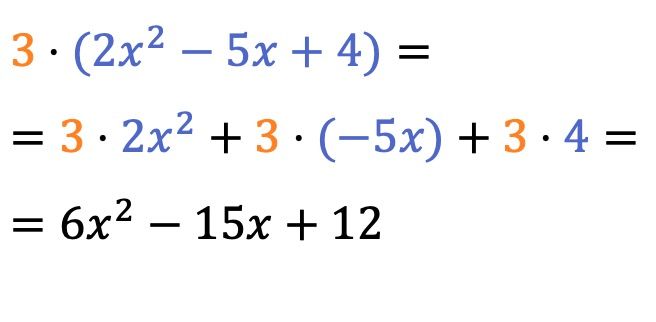
يمكن حذف علامة الضرب الموجودة أمام القوسين.

$\begin{array}{l} 2\cdot (5x^4-6x^2) = \\[2ex] =2 (5x^4-6x^2)= \\[2ex] = 10x^4-12x^2 \end{array}$

ضرب كثيرة الحدود في أحادية الحد

قبل أن نرى كيفية ضرب كثيرة الحدود في أحادية الحد، سنتذكر أولًا كيفية ضرب وحيدات الحد مع بعضها البعض، لأنك تحتاج إلى معرفتها لتتمكن من إجراء هذا النوع من العمليات كثيرة الحدود.

يتكون حاصل ضرب وحيدتي الحد من ضرب معاملاتهما مع بعضهما البعض وأجزائهما الحرفية فيما بينهما، أي أنه يتم ضرب معاملات وحيدات الحد وإضافة أسس المتغيرات التي لها نفس الأساس. ننظر إلى المثال التالي:

$3x^2 \cdot 4x^5 = (3\cdot 4) x^{2+5} = 12x^7$

الآن دعونا نرى كيفية ضرب أحادية الحد في كثيرة الحدود:

في الرياضيات، لحل عملية ضرب أحادية الحد في كثيرة الحدود، يتم ضرب أحادية الحد في كل حد في كثيرة الحدود.

كما في السابق، يمكن أيضًا حذف علامة الضرب:

$\begin{array}{l} -4x \cdot (2x^3-5x^2)= \\[2ex] =-4x (2x^3-5x^2)=\\[2ex] = -4x\cdot 2x^3 -4x \cdot (-5x^2) = \\[2ex] =-8x^4 +20x^3 \end{array}$

لاحظ في المثال السابق أنه عند ضرب أحاديات الحد أو متعددات الحدود، يجب عليك أيضًا مراعاة قاعدة العلامات. في الواقع، هناك خطأ شائع جدًا عند ضرب أحاديات الحد ومتعددات الحدود وهو الحصول على إشارة خاطئة للحد.

بالتأكيد في مرحلة ما، عندما رأيت شيئًا جديدًا في الرياضيات، سألت نفسك: ما الغرض منه ؟ حسنًا، يُستخدم هذا النوع من الضرب للحصول على العامل المشترك لكثيرة الحدود ، وهي عملية تسمح لك بتبسيط كثيرات الحدود (مفيدة جدًا). يمكنك أن ترى ما هو وكيف يتم حساب العامل المشترك لكثيرة الحدود في هذا الرابط.

ضرب اثنين من كثيرات الحدود

بمجرد أن نعرف كيفية ضرب كثيرات الحدود بالأرقام ووحيدات الحد، دعونا نرى ما هي وكيفية ضرب كثيرات الحدود في كثيرات الحدود.

لضرب كثيرات الحدود، اتبع الخطوات التالية:

اضرب كل حد في كثيرة الحدود الأولى بجميع الحدود في كثيرة الحدود الثانية.
إضافة (أو طرح) وحيدات الحد من نفس الدرجة (وحيدات الحد المماثلة).

حتى تتمكن من معرفة ماهية هذه الطريقة بالضبط، سنحل عملية ضرب كثيرات الحدود التالية خطوة بخطوة:

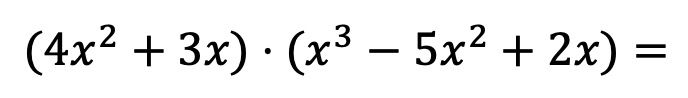
أولًا، يجب علينا ضرب كل عنصر من كثيرة الحدود الأولى في كل حد من كثيرة الحدود الثانية:

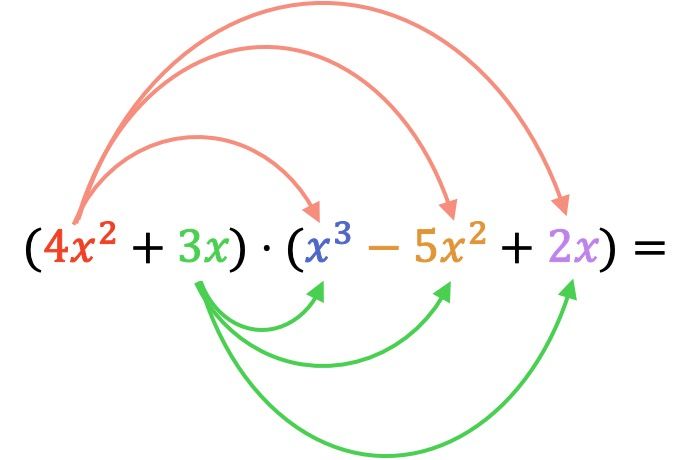
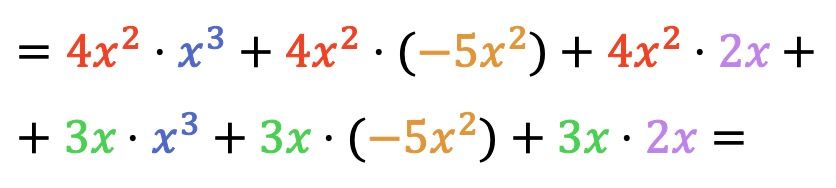
الآن نقوم بجميع عمليات ضرب أحاديات الحد:

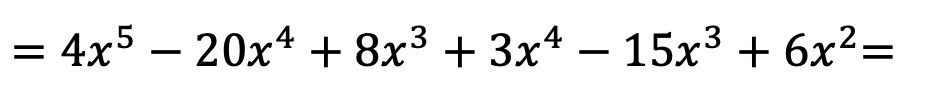
بمجرد ضرب كثيرات الحدود معًا، علينا فقط تجميع الحدود الناتجة المتشابهة، أي الحدود التي لها نفس الحرف ونفس الأس:

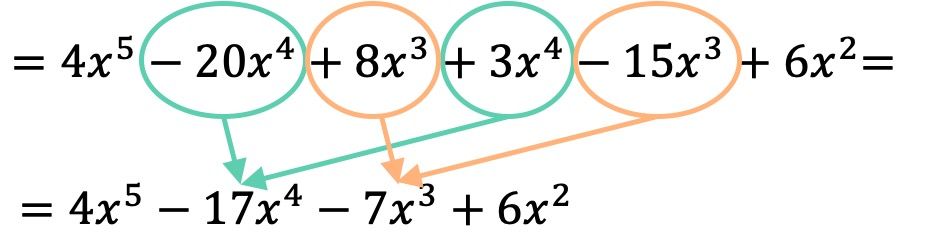
وبالتالي فإن نتيجة ضرب كثيرات الحدود هي:

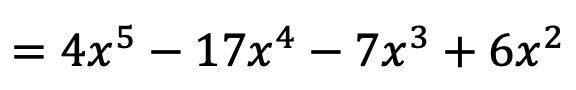
وبهذه الطريقة نكون قد حسبنا بالفعل ضرب كثيرات الحدود. ربما يبدو الأمر صعبًا جدًا بالنسبة لك الآن، لكنك ستلاحظ أنه عندما تتدرب بتمرينين أو ثلاثة سيكون الأمر أسهل بكثير.

الآن بعد أن رأيت كيف يتم حل الضرب بين كثيرات الحدود، ربما تكون مهتمًا بمعرفة كيفية قسمة كثيرات الحدود . في الواقع، قسمة كثيرات الحدود أكثر تعقيدًا بكثير من ضربها، ولهذا السبب قمنا بشرح الإجراء (والنصائح😉) خطوة بخطوة حتى تتمكن من فهمه بالكامل. إذا كنت مهتمًا، فانقر على هذا الرابط لترى كيفية تقسيم كثيرات الحدود.

الضرب متعدد الحدود العمودي

لقد رأينا للتو كيفية ضرب كثيرة الحدود في كثيرة حدود أخرى أفقيًا، ولكن يمكن أيضًا القيام بذلك بطريقة أكثر كلاسيكية: ضرب كثيرات الحدود رأسيًا. دعونا نرى كيف يتم استخدام هذه الطريقة من خلال حل مثال لضرب كثيرات الحدود.

إذا أردنا ضرب كثيرتي الحدود التاليتين رأسيًا:

$(5x^2+3x-4) \cdot (2x^2-x)$

أول شيء يتعين علينا القيام به هو وضع كثيرة الحدود أسفل الأخرى، كضرب جبري لكثيرات الحدود:

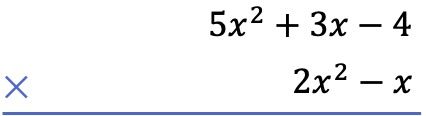
ثانياً، نضرب كل حد من كثيرة الحدود أدناه في كل حد من كثيرة الحدود أعلاه، ونضع النتائج مرتبة حسب الأعمدة من أعلى درجة إلى أدنى درجة:

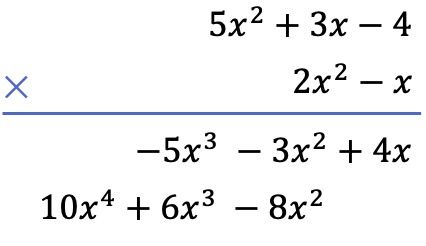
وأخيرًا، نضيف الحدود المحاذاة رأسيًا:

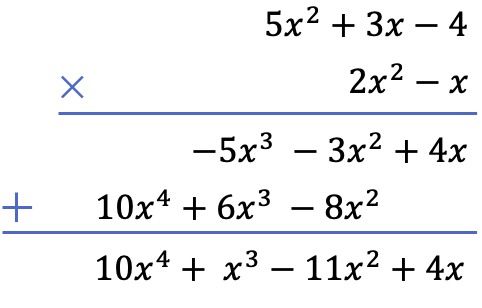
الآن بعد أن رأيت الطريقتين الموجودتين لحل عملية ضرب كثيرات الحدود، هل تعلم أنه يمكنك أيضًا ضرب الكسور في كثيرات الحدود ؟ وليس الضرب فقط، بل يمكن إجراء جميع أنواع العمليات باستخدام هذه الأنواع من الكسور. انقر على هذا الرابط واكتشف ما هي الكسور الجبرية .

خصائص الضرب متعدد الحدود

ضرب كثيرات الحدود له الخصائص التالية:

الخاصية التبادلية : ترتيب ضرب كثيرات الحدود لا يغير نتيجة الضرب.

$P(x)\cdot Q(x) = Q(x) \cdot P(x)$

الخاصية الترابطية : عند ضرب ثلاث كثيرات حدود أو أكثر، تكون نتيجة الضرب هي نفسها بغض النظر عن كيفية تجميع العوامل:

$\bigl(P(x) \cdot Q(x)\bigr) \cdot R(x) =P(x) \cdot \bigl(Q(x) \cdot R(x)\bigr)$

خاصية التوزيع : مجموع كثيرتي الحدود مضروبًا في الثلث يساوي مجموع كل إضافة مضروبًا في كثيرة الحدود الثالثة.

$P(x)\cdot \bigl(Q(x)+ R(x)\bigr) = P(x)\cdot Q(x) + P(x) \cdot R(x)$

درجة كثيرة الحدود الناتجة عن الضرب بين كثيرتي الحدود تساوي مجموع درجات كثيرتي الحدود المضروبة.

تمارين محلولة على ضرب كثيرات الحدود

لكي تتمكن من التدرب، أتركك مع العديد من التمارين المحلولة حول ضرب كثيرات الحدود. يمكنك محاولة حلها بنفسك والتحقق من نتائجك باستخدام الحل المقترح. يمكنك بعد ذلك أن تطرح علينا جميع أسئلتك في التعليقات، وسنكون سعداء بمساعدتك.

التمرين 1

احسب المنتجات التالية بين كثيرات الحدود والعددية:

$\text{A)} \ 4\cdot (2x^3-4x)$

$\text{B)} \ -3 \cdot (-5x^2+9x)$

$\text{C)} \ 5\cdot(3x^2+4x-7)$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7)$

انظر الحل

لحساب ضرب كثيرة الحدود في رقم، يجب عليك ضرب الرقم في معامل كل عنصر من عناصر كثيرة الحدود. لذا:

$\text{A)} \ 4\cdot (2x^3-4x) =4 \cdot 2x^3 -4\cdot 4x = \bm{8x^3-16x}$

$\text{B)} \ -3 \cdot (-5x^2+9x) = -3 \cdot (-5x^2)-3\cdot 9x = \bm{15x^2-27x}$

$\text{C)} \ 5\cdot(3x^2+4x-7) = \bm{15x^2+20x-35}$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7) = \bm{-24x^5+36x^3-48x^2+42}$

تمرين 2

حل الضربات التالية بين كثيرات الحدود ووحيدات الحد:

$\text{A)} \ 2x \cdot (5x^2+3)$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5)$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x)$

انظر الحل

لحل عملية ضرب كثيرة الحدود في أحادية الحد، يجب عليك ضرب أحادية الحد المذكورة في كل حد من حدود كثيرة الحدود. لذا:

$\text{A)} \ 2x \cdot (5x^2+3) = 2x \cdot 5x^2+2x\cdot 3 = \bm{10x^3+6x}$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)= -4x^2 \cdot 6x^4 - 4x^2 \cdot (-9x^2) = \bm{-24x^6+36x^4}$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5) = \bm{10x^6-10x^5+25x^3}$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x) = \bm{21x^8-12x^7-3x^5-9x^3}$

التمرين 3

حدد نتيجة الضرب التالي بين كثيرات الحدود:

$\text{A)} \ (4x^2 + 1) \cdot (3x^2-2)$

$\text{B)} \ (-3x^4+2x) \cdot (5x^4-x)$

$\text{C)} \ (2x^3-5x^2)\cdot (4x-7)$

انظر الحل

لحساب ضرب كثيرتي الحدود، علينا ضرب كل عنصر من كثيرة الحدود الأولى في كل عنصر من كثيرة الحدود الثانية ثم تجميع الحدود المتشابهة معًا. لذا:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2 + 1) \cdot (3x^2-2) = \\[2ex] =4x^2 \cdot 3x^2 +4x^2\cdot (-2) +1 \cdot 3x^2 +1 \cdot (-2) = \\[2ex] = 12x^4-8x^2+3x^2 -2 = \\[2ex] = \bm{12x^4-5x^2-2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (-3x^4+2x) \cdot (5x^4-x) = \\[2ex] =-3x^4\cdot 5x^4 -3x^4\cdot (-x) +2x \cdot 5x^4 +2x \cdot (-x) = \\[2ex] = -15x^8+3x^5+10x^5-2x^2 = \\[2ex] = \bm{-15x^8+13x^5-2x^2} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^3-5x^2)\cdot (4x-7) = \\[2ex] =2x^3\cdot 4x +2x^3\cdot (-7) -5x^2 \cdot 4x -5x^2\cdot (-7) = \\[2ex] = 8x^4-14x^3-20x^3+35x^2 = \\[2ex] = \bm{8x^4-34x^3+35x^2} \end{array}$

التمرين 4

أوجد نتيجة الضرب التالي بين كثيرات الحدود:

$\text{A)} \ (4x^2-6x+2) \cdot (5x^3-x^2)$

$\text{B)} \ (3x^3-2x+7) \cdot (-4x^3+5x)$

$\text{C)} \ (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3)$

انظر الحل

لحساب ضرب كثيرتي الحدود، نحتاج إلى ضرب كل عنصر من كثيرة الحدود الأولى في كل عنصر من كثيرة الحدود الثانية، ثم إضافة الحدود المتشابهة. لذا:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2-6x+2) \cdot (5x^3-x^2) = \\[2ex] =4x^2 \cdot 5x^3 +4x^2\cdot (-x^2) -6x \cdot 5x^3 -6x \cdot (-x^2) + 2 \cdot 5x^3 +2 \cdot (-x^2) = \\[2ex] = 20x^5-4x^4-30x^4+6x^3+10x^3-2x^2 = \\[2ex] = \bm{20x^5-34x^4+16x^3-2x^2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (3x^3-2x+7) \cdot (-4x^3+5x) = \\[2ex] =3x^3 \cdot (-4x^3) +3x^3\cdot 5x -2x \cdot (-4x^3) -2x \cdot 5x + 7 \cdot (-4x^3) +7 \cdot 5x = \\[2ex] =-12x^6+15x^4+8x^4-10x^2-28x^3+35x = \\[2ex] = \bm{-12x^6+23x^4-28x^3-10x^2+35x} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3) = \\[2ex] = 18x^9-36x^8-45x^7-8x^8+16x^7+20x^6+2x^7-4x^6-5x^5 = \\[2ex] = \bm{18x^9-44x^8-27x^7+16x^6-5x^5} \end{array}$

التمرين 5

احسب مضاعفات كثيرات الحدود التالية:

$\text{A)} \ (2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)$

$\text{B)} \ (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)$

$\text{C)} \ (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8)$

انظر الحل

لإنشاء منتج من كثيرتي الحدود، يجب عليك ضرب كل حد من كثيرة الحدود الأولى في كل حد من كثيرة الحدود الثانية، ثم تجميع أحاديات الحد المتشابهة التي تم الحصول عليها. حتى الآن:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l}(2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)= \\[2ex] = 8x^6-12x^5+12x^5-18x^4-24x^4+36x^3+20x^3-30x^2-4x^2+6x = \\[2ex] = \bm{8x^6-42x^4+56x^3-34x^2+6x} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)= \\[2ex] =-x^5-5x^4+2x^3+9x^2+4x^4+20x^3-8x^2-36x-7x^3-35x^2+14x+63 = \\[2ex] = \bm{-x^5-x^4+15x^3-34x^2-22x+63} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8) = \\[2ex] = 8x^{13}-16x^{10}-2x^9+16x^7+24x^{11}-48x^8-6x^7+48x^5+ \\[2ex] + \ 12x^{10}-24x^7-3x^6+24x^4-20x^8+40x^5+5x^4-40x^2 = \\[2ex] = \bm{8x^{13}+24x^{11}-4x^{10}-2x^9-68x^8-14x^7-3x^6+} \\[2ex] \bm{+ \ 88x^5+29x^4-40x^2} \end{array}$

التمرين 6

حل عملية الضرب التالية لثلاث كثيرات الحدود:

$(2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x)$

انظر الحل

تتكون عملية المشكلة من ضربين لكثيرات الحدود، وبشكل أكثر دقة، فهي تتكون من اثنين من ذات الحدين وثلاثية الحدود. لذا، علينا أولًا إيجاد حاصل الضرب ثم ضرب الناتج في كثيرة الحدود المتبقية.

لذلك نحسب الضرب الأول:

$\begin{array}{l} (2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x) = \\[2ex] = \bigl[-10x^6+6x^4-12x^2+15x^4-9x^2+18 \bigr]\cdot (9x^3-6x) = \\[2ex] = (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)\end{array}$

والآن نحل عملية الضرب المتبقية:

$\begin{array}{l} (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)= \\[2ex] = -90x^9+60x^7+189x^7-126x^5-189x^5+126x^3+162x^3-108x \\[2ex] =\bm{-90x^9+249x^7-315x^5+288x^3-108x} \end{array}$

التمرين 7

اضرب كثيرات الحدود التالية بمعاملات عقلانية (مع الكسور):

$\displaystyle \left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right)$

انظر الحل

على الرغم من أن كثيرات الحدود تحتوي على كسور، إلا أنها لا تزال عبارة عن ضرب بين كثيرتي الحدود. ولذلك يجب حلها مثل أي منتج متعدد الحدود: اضرب جميع العناصر معًا ثم قم بتجميع أحاديات الحد المتشابهة.

لذلك نحن نضرب كثيرات الحدود:

$\displaystyle \begin{array}{l} \displaystyle\left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right) = \\[4ex] = \displaystyle\frac{1}{3}x^2 \cdot 5x +\frac{1}{3}x^2\cdot \left(- \frac{2}{7} \right) -4x \cdot 5x - 4x \cdot \left(- \frac{2}{7} \right) = \\[4ex] =\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x\end{array}$

وأخيرًا، نضيف (أو نطرح) المصطلحات التي تتطابق أجزاؤها الحرفية:

$\begin{array}{l}\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x= \\[4ex] \displaystyle= \frac{5}{3}x^3 -\frac{2}{21}x^2 -\frac{420}{21}x^2+\frac{8}{7} x \\[4ex] \displaystyle=\mathbf{\frac{5}{3}}\bm{x^3} -\mathbf{\frac{422}{20}}\bm{x^2}+\mathbf{\frac{8}{7}} \bm{x} \end{array}$

لإكمال هذا التمرين بنجاح، كان من المهم أن تتقن العمليات المتعلقة بالكسور. ولكن إذا كان لديك أي أسئلة حول أي خطوة، يمكنك طرحها في التعليقات وسوف نقوم بالرد عليها في أسرع وقت ممكن.

الضرب (أو المنتج) من كثيرات الحدود

ضرب كثير الحدود برقم

ضرب كثيرة الحدود في أحادية الحد

ضرب اثنين من كثيرات الحدود

الضرب متعدد الحدود العمودي

خصائص الضرب متعدد الحدود

تمارين محلولة على ضرب كثيرات الحدود

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

التمرين 7

اترك تعليقاً إلغاء الرد