ضرب المصفوفة

سنرى في هذه الصفحة كيفية ضرب المصفوفات ذات الأبعاد 2×2، 3×3، 4×4، إلخ. نشرح عملية ضرب المصفوفات خطوة بخطوة من خلال مثال، ثم ستجد تمارين محلولة لتتمكن من التدرب عليها أيضًا. وأخيرًا، سوف تتعلم متى لا يمكن ضرب مصفوفتين، وستتعرف على جميع خصائص عملية المصفوفة هذه.

كيفية ضرب مصفوفتين؟

دعونا نرى الإجراء الخاص بإجراء ضرب مصفوفتين مع مثال:

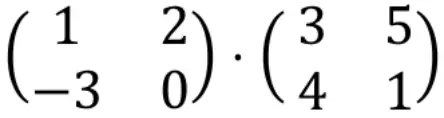
لحساب ضرب المصفوفة، يجب ضرب صفوف المصفوفة اليسرى في أعمدة المصفوفة اليمنى.

لذا علينا أولًا ضرب الصف الأول في العمود الأول. للقيام بذلك، نضرب كل عنصر في الصف الأول في كل عنصر في العمود الأول واحدًا تلو الآخر، ثم نضيف النتائج. كل هذا سيكون العنصر الأول في الصف الأول من المصفوفة الناتجة. انظر إلى الإجراء:

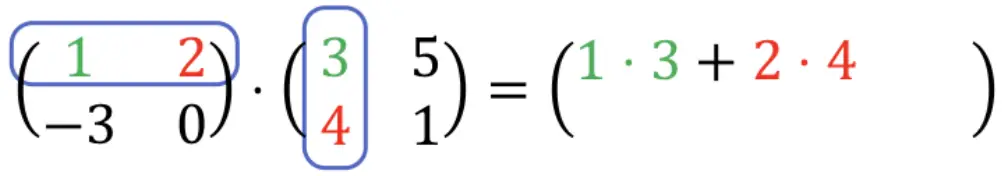
كيفية حل ضرب المصفوفات 2x2، والعمليات مع المصفوفات

1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11. إذن:

الآن نحن بحاجة إلى ضرب الصف الأول في العمود الثاني . ولذلك نكرر الإجراء: نضرب كل عنصر من عناصر الصف الأول واحدًا تلو الآخر في كل عنصر من عناصر العمود الثاني، ثم نضيف النتائج. وكل هذا سيكون العنصر الثاني من الصف الأول من المصفوفة الناتجة:

1 ⋅ 5 + 2 ⋅ 1 = 5 + 2 = 7. إذن:

بمجرد أن نملأ الصف الأول من المصفوفة الناتجة، ننتقل إلى الصف الثاني. لذلك نضرب الصف الثاني في العمود الأول بتكرار الإجراء: نضرب كل عنصر من عناصر الصف الثاني في كل عنصر من عناصر العمود الأول واحدًا تلو الآخر، ونضيف النتائج:

-3 ⋅ 3 + 0 ⋅ 4 = -9 + 0 = -9. حتى الآن:

وأخيرا، نقوم بضرب الصف الثاني في العمود الثاني . دائمًا بنفس الإجراء: نضرب كل عنصر من عناصر الصف الثاني واحدًا تلو الآخر في كل عنصر من عناصر العمود الثاني، ثم نضيف النتائج:

-3 ⋅ 5 + 0 ⋅ 1 = -15 + 0 = -15. حتى الآن:

وهنا ينتهي ضرب المصفوفتين. كما رأيت، تحتاج إلى ضرب الصفوف في الأعمدة، مع تكرار نفس الإجراء دائمًا: ضرب كل عنصر من عناصر الصف في كل عنصر من عناصر العمود واحدًا تلو الآخر، ثم قم بإضافة النتائج.

حل تمارين ضرب المصفوفات

التمرين 1

حل منتج المصفوفة التالي:

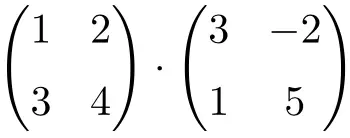
تمرين تم حله خطوة بخطوة لمصفوفات 2x2، العمليات على المصفوفات

انظر الحل

إنه منتج مصفوفات من الرتبة 2:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}$

لحل منتج المصفوفة، يجب عليك ضرب صفوف المصفوفة اليسرى بأعمدة المصفوفة اليمنى.

لذلك، نقوم أولاً بضرب الصف الأول في العمود الأول. للقيام بذلك، نضرب كل عنصر في الصف الأول في كل عنصر في العمود الأول واحدًا تلو الآخر، ثم نضيف النتائج. وكل هذا سيكون العنصر الأول في الصف الأول من المصفوفة الناتجة:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}$

الآن دعونا نضرب الصف الأول في العمود الثاني للحصول على العنصر الثاني من الصف الأول من المصفوفة الناتجة:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}$

ننتقل إلى الصف الثاني، فنضرب الصف الثاني في العمود الأول:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}$

وأخيراً نقوم بضرب الصف الثاني في العمود الثاني لحساب العنصر الأخير في الجدول:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}$

وبالتالي فإن نتيجة ضرب المصفوفة هي:

$\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}$

تمرين 2

أوجد نتيجة ضرب المصفوفة المربعة 2×2 التالية:

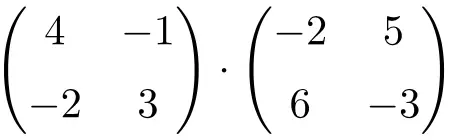
تمرين تم حله خطوة بخطوة في ضرب المصفوفات 2x2، عمليات المصفوفات

انظر الحل

إنه منتج مصفوفات البعد 2 × 2.

لحل عملية الضرب، عليك ضرب صفوف المصفوفة اليسرى في أعمدة المصفوفة اليمنى:

$\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}$

التمرين 3

احسب ضرب المصفوفة 3×3 التالية:

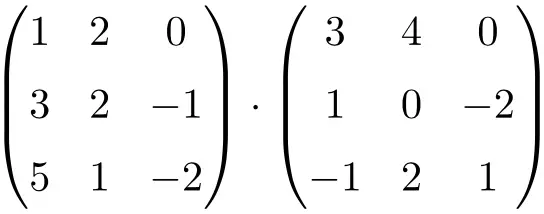
تمرين تم حله خطوة بخطوة، ضرب المصفوفات 3x3، عمليات المصفوفة

انظر الحل

لإجراء عملية ضرب المصفوفة 3×3، يجب عليك ضرب صفوف المصفوفة اليسرى في أعمدة المصفوفة اليمنى:

$\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}$

التمرين 4

نظرا للمصفوفة

$A$

$\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}$

احسب:

$\displaystyle 2A\cdot A^t$

انظر الحل

سنقوم أولاً بحساب مصفوفة النقل لـ

$A$

للقيام بالضرب. ولإنشاء مصفوفة تبديل، نحتاج إلى تغيير الصفوف إلى أعمدة. أي أن الصف الأول من المصفوفة يصبح العمود الأول من المصفوفة والصف الثاني من المصفوفة يصبح العمود الثاني من المصفوفة. حتى الآن:

$\displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

وبالتالي تظل عملية المصفوفة كما يلي:

$\displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

الآن يمكننا أن نفعل الحسابات. نحسب أولا

$2A$

(على الرغم من أنه يمكننا أيضًا الحساب أولاً

$A \cdot A^t$

$\displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

وأخيرًا، نحل حاصل ضرب المصفوفات:

$\displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =$

$\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}$

التمرين 5

النظر في المصفوفات التالية:

$\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}$

احسب:

$\displaystyle A\cdot B - B \cdot A$

انظر الحل

هي عملية تجمع بين الطرح وضرب المصفوفات من الرتبة 2:

$\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

نحسب أولاً الضرب على اليسار:

$\displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =$

$\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

الآن نحل الضرب على اليمين:

$\displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}$

وأخيرًا نطرح المصفوفات:

$\displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}$

متى لا يمكنك ضرب مصفوفتين؟

لا يمكن ضرب جميع المصفوفات. لضرب مصفوفتين، يجب أن يتطابق عدد الأعمدة في المصفوفة الأولى مع عدد الصفوف في المصفوفة الثانية.

على سبيل المثال، لا يمكن إجراء الضرب التالي لأن المصفوفة الأولى تحتوي على 3 أعمدة والمصفوفة الثانية تحتوي على صفين:

$\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}$

لكن إذا عكسنا الترتيب، فيمكن مضاعفة العدد. لأن المصفوفة الأولى تحتوي على عمودين والمصفوفة الثانية تحتوي على صفين:

$\displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}$

خصائص ضرب المصفوفات

يتميز هذا النوع من عمليات المصفوفة بالخصائص التالية:

ضرب المصفوفة هو ترابطي:

$\displaystyle \left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)$

الضرب في المصفوفة له أيضًا خاصية التوزيع:

$\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C$

منتج المصفوفات ليس تبادليًا:

$\displaystyle A \cdot B \neq B \cdot A$

على سبيل المثال، ضرب المصفوفة التالية يعطي النتيجة:

$\displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}$

لكن نتيجة الضرب تختلف إذا عكسنا ترتيب ضرب المصفوفات:

$\displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}$

بالإضافة إلى ذلك، أي مصفوفة مضروبة في مصفوفة الهوية ينتج عنها نفس المصفوفة. وهذا ما يسمى خاصية الهوية المضاعفة:

$\displaystyle A \cdot I=A$

$\displaystyle I \cdot A=A$

على سبيل المثال:

$\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}$

أخيرًا، كما قد تخمن بالفعل، أي مصفوفة مضروبة في المصفوفة الصفرية تساوي المصفوفة الصفرية. وهذا ما يسمى خاصية الضرب للصفر:

$\displaystyle A \cdot 0=0$

$\displaystyle 0\cdot A=0$

على سبيل المثال:

$\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}$

كيفية ضرب مصفوفتين؟

حل تمارين ضرب المصفوفات

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

متى لا يمكنك ضرب مصفوفتين؟

خصائص ضرب المصفوفات

اترك تعليقاً إلغاء الرد