صيغة المسافة بين نقطتين (هندسة)

ستجد في هذه الصفحة كيفية حساب المسافة بين نقطتين في الهندسة (الصيغة). ستتمكن أيضًا من رؤية الأمثلة، بالإضافة إلى التدرب على حل تمارين المسافة بين نقطتين.

ما هي صيغة المسافة بين نقطتين؟

المسافة بين نقطتين تساوي طول القطعة التي تربطهما. لذلك، في الرياضيات، لتحديد المسافة بين نقطتين مختلفتين، يجب علينا حساب مربعات الاختلافات بين إحداثياتهما ثم إيجاد جذر مجموع المربعات المذكورة.

بمعنى آخر، الصيغة المستخدمة لحساب المسافة بين نقطتين مختلفتين على المستوى الديكارتي هي كما يلي:

النظر في إحداثيات نقطتين متميزتين:

$A(x_1,y_1) \qquad \qquad B(x_2,y_2)$

صيغة المسافة بين نقطتين هي:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

هذه الصيغة تأتي من حجم المتجه. في الواقع، ما نفعله بهذه الصيغة هو حساب مقدار المتجه الذي تحدده النقطتان المعنيتان. يمكنك قراءة المزيد عن هذا في شرح ما هو معامل المتجه .

من ناحية أخرى، في الهندسة التحليلية، يمكن أيضًا توضيح صيغة المسافة بين نقطتين باستخدام نظرية فيثاغورس:

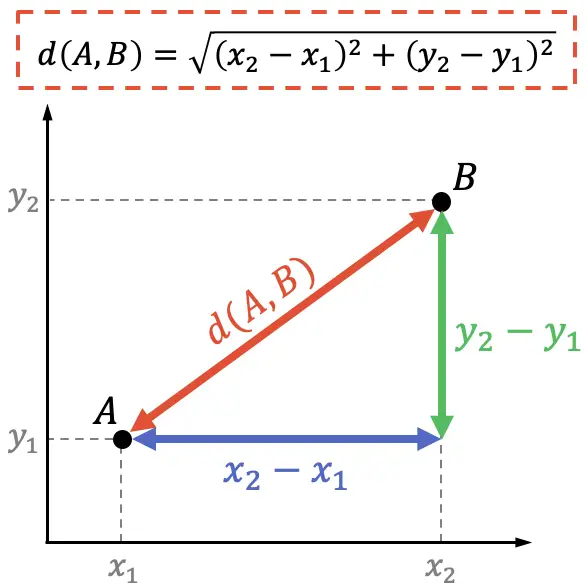
تنص نظرية فيثاغورس على أن مربع الوتر في المثلث القائم الزاوية يساوي مجموع مربعي ساقيه، وبالتالي:

$\bigl(d(A,B)\bigr)^2 = (x_2-x_1)^2 + (y_2-y_1)^2$

وللحصول على الصيغة عليك فقط إيجاد المسافة بين النقطتين:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

أخيرًا، تجدر الإشارة إلى أنه إذا كنا نعمل مع نقاط ذات إحداثيات ثلاثية، فإن صيغة المسافة بين نقطتين في الفضاء (في R3) ستكون نفسها ولكن بإضافة الإحداثي Z:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2 \vphantom{\frac{1}{2}}}$

مثال لحساب المسافة بين نقطتين

بعد أن رأينا تعريف صيغة المسافة بين نقطتين، دعونا نرى الآن كيفية تحديد المسافة المذكورة باستخدام مثال:

أوجد المسافة بين النقطتين التاليتين:

$A(-1,7) \qquad \qquad B(3,4)$

لإيجاد المسافة بين النقطتين هندسيًا، ما عليك سوى تطبيق الصيغة:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

الآن نعوض إحداثيات النقاط في الصيغة:

$d(A,B) = \sqrt{(3-(-1))^2+(4-7)^2 \vphantom{\frac{1}{2}}}$

ونقوم بالحسابات:

$\begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}$

وبالتالي فإن المسافة بين النقطتين تساوي 5 وحدات.

ومن الواضح أن قيمة المسافة يجب أن تعطينا دائمًا إشارة موجبة، لأن المسافات تكون موجبة دائمًا. وإلا فهذا يعني أننا ارتكبنا خطأ في خطوة ما.

استكشاف الأخطاء وإصلاحها المسافة بين نقطتين

التمرين 1

احسب المسافة بين النقطتين التاليتين:

$A(4,2) \qquad \qquad B(1,5)$

انظر الحل

للعثور على المسافة الهندسية بين النقطتين، ما عليك سوى استخدام الصيغة:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

الآن نعوض إحداثيات النقاط في الصيغة:

$d(A,B) = \sqrt{(1-4)^2+(5-2)^2 \vphantom{\frac{1}{2}}}$

ونقوم بالحسابات:

$\begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}$

تمرين 2

أوجد المسافة بين النقطتين التاليتين:

$A(8,6) \qquad \qquad B(-4,1)$

انظر الحل

للعثور على المسافة الرياضية بين النقطتين، يجب علينا استخدام الصيغة المقابلة:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

الآن نعوض إحداثيات النقاط في الصيغة:

$d(A,B) = \sqrt{(-4-8)^2+(1-6)^2 \vphantom{\frac{1}{2}}}$

ونقوم بالحسابات:

$\begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}$

التمرين 3

احسب محيط المثلث المكون من النقاط A وB وC الموضحة بيانياً أدناه:

انظر الحل

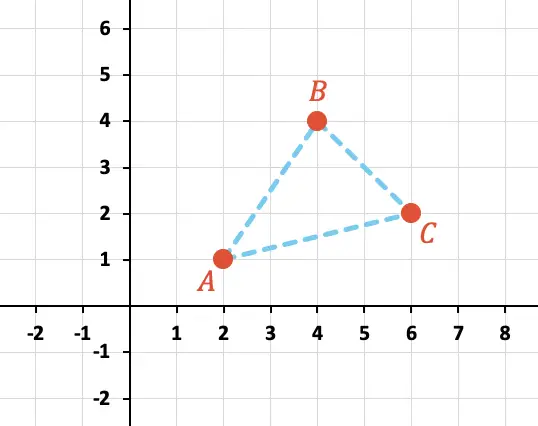
أولاً، نحتاج إلى تحديد إحداثيات X وY لكل نقطة على الرسم البياني:

$A(2,1)$

$B(4,4)$

$C(6,2)$

والآن نحتاج إلى حساب المسافة بين جميع النقاط باستخدام الصيغة:

$d(A,B) = \sqrt{(4-2)^2+(4-1)^2 } = \sqrt{4+9} =\sqrt{13} = 3,61$

$d(A,C) = \sqrt{(6-2)^2+(2-1)^2 } = \sqrt{16+1} =\sqrt{17} = 4,12$

$d(B,C) = \sqrt{(6-4)^2+(2-4)^2 } = \sqrt{4+4} =\sqrt{8} = 2,83$

إذن محيط المثلث سيكون مجموع أطوال أضلاعه الثلاثة:

$P=3,61+4,12+2,83= \bm{10,56}$

التمرين 4

تحقق مما إذا كان المثلث الذي رؤوسه النقاط A وB وC مثلثًا متساوي الساقين. لكن النقاط الثلاث:

$A(-4,5) \qquad B(7,-5) \qquad C(10,0)$

انظر الحل

لكي يكون المثلث متساوي الساقين، يجب أن يكون ضلعان منه متساويين. ومن ثم، علينا إيجاد طول كل ضلع من أضلاعه، وهو ما يتوافق مع المسافات بين رءوسه.

لذلك نحسب المسافة بين رؤوس المثلث:

$d(A,B) = \sqrt{(7-(-4))^2+(-5-5)^2 } = \sqrt{11^2+(-10)^2} = \sqrt{221}$

$d(A,C) = \sqrt{(10-(-4))^2+(0-5)^2 } = \sqrt{14^2+(-5)^2} = \sqrt{221}$

$d(B,C) = \sqrt{(10-7)^2+(0-(-5))^2} = \sqrt{3^2+5^2} = \sqrt{34}$

إذن، المثلث له ضلعان متماثلان وقياس الضلع الثالث مختلف عن الضلعين الآخرين، فهو في الواقع مثلث متساوي الساقين.

التمرين 5

أوجد نقطة على المحور Y تكون متساوية البعد عن النقطتين التاليتين:

$A(5,-3) \qquad \qquad B(-2,4)$

انظر الحل

أولًا، إذا كانت النقطة تقع على محور الكمبيوتر (محور OY) فهذا يعني أن حدود النقطة تساوي صفرًا:

$P(0,y)$

ثانياً، إذا كانت النقطة متساوية البعد عن النقطتين A وB، فهذا يعني أن المعادلة التالية قد تحققت:

$d(P,A)= d(P,B)$

لذا، باستخدام صيغة المسافة بين نقطتين، يمكننا إيجاد قيمة المتغير y من المعادلة السابقة:

$\sqrt{(5-0)^2+(-3-y)^2 \vphantom{\frac{1}{2}}}=\sqrt{(-2-0)^2+(4-y)^2 \vphantom{\frac{1}{2}}}$

بما أن طرفي المعادلة لهما جذر، فيمكننا تبسيطهما:

$5^2+(-3-y)^2=(-2)^2+(4-y)^2$

نحن نحل القوى والمساواة البارزة (أو المنتجات البارزة):

$25+9+y^2+6y=4+16+y^2-8y$

ونعمل حتى نجد قيمة المجهول y :

$y^2+6y-y^2+8y=4+16-25-9$

$14y=-14$

$y=\cfrac{-14}{14}$

$y=-1$

باختصار، النقطة التي طرحها علينا بيان المشكلة هي:

$\bm{P(0,-1)}$

إذا وجدت هذه المقالة مفيدة، فمن المحتمل أن تكون مهتمًا أيضًا بتمارين المسافة بين النقطة والخط . في الصفحة المرتبطة لن تجد فقط تمارين محلولة خطوة بخطوة، بل ستجد أيضًا شرحًا تفصيليًا لحساب المسافة بين النقاط والخطوط، وأمثلة وتطبيق صيغة المسافة بين نقطة وخط لتحديد نوع آخر من المسافة .

ما هي صيغة المسافة بين نقطتين؟

مثال لحساب المسافة بين نقطتين

استكشاف الأخطاء وإصلاحها المسافة بين نقطتين

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد