▷ حل عدم التحديد الصفري بين الصفر (0/0)

نشرح في هذه المقالة كيفية حفظ نهاية الدالة عندما تعطي عدم اليقين 0/0. بالإضافة إلى ذلك، ستتمكن من التدرب على تمارين محلولة على عدم تعيين صفر بين صفر.

كيفية حل عدم التحديد الصفري بين الصفر (0/0)

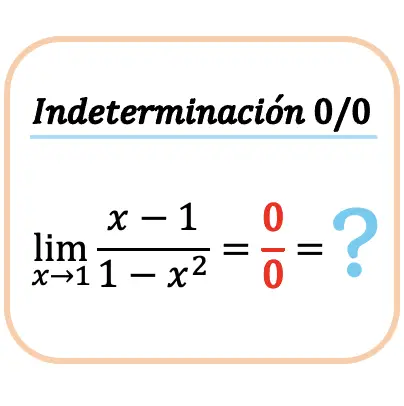
سنرى بعد ذلك كيفية حساب نهاية الدالة عندما تعطي عدم تحديد صفر بين الصفر (0/0). للقيام بذلك، سوف نقوم بحساب مثال خطوة بخطوة:

$\displaystyle\lim_{x \to 2} \frac{x^2-x-2}{x^2-3x+2}$

نحاول أولًا حساب النهاية عن طريق استبدال قيمة x في الدالة:

$\displaystyle\lim_{x \to 2} \frac{x^2 - x -2}{x^2-3x+2}=\frac{2^2 -2-2}{2^2-3\cdot 2+2}=\frac{0}{0}$

لكننا نحصل على عدم التعيين 0 مقسومًا على 0.

عندما تعطي نهاية دالة النقطة حالة عدم اليقين 0/0 ، فمن الضروري تحليل كثيرات الحدود للبسط والمقام ثم تبسيط العوامل المشتركة.

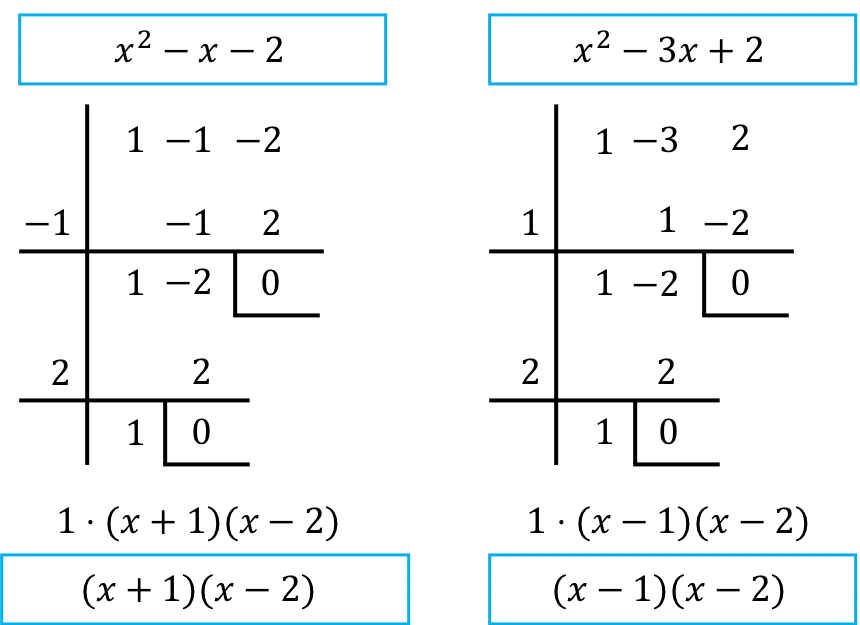
ومن ثم، يجب علينا تحليل كثيرات حدود بسط الكسر ومقامه. للقيام بذلك، نستخدم قاعدة روفيني:

➤ إذا كنت لا تعرف كيفية تحليل كثيرات الحدود إلى عوامل ، ننصحك بالاطلاع على الشرح على موقعنا المتخصص في كثيرات الحدود: www.polinomios.org

وبالتالي، بمجرد تحليل كثيرات الحدود، تصبح النهاية كما يلي:

$\displaystyle\lim_{x \to 2} \cfrac{x^2-x-2}{x^2-3x+2}=\lim_{x \to 2}\frac{(x+1)(x-2)}{(x-1)(x-2)}$

يمكننا الآن تبسيط النهاية عن طريق حذف العوامل المتكررة في بسط الكسر ومقامه:

$\displaystyle\lim_{x \to 2} \cfrac{(x+1)\cancel{(x-2)}}{(x-1)\cancel{(x-2)}}=\lim_{x \to 2} \cfrac{(x+1)}{(x-1)}$

وأخيرًا، نعيد حساب الحد:

$\displaystyle\lim_{x \to 2} \cfrac{x+1}{x-1}=\cfrac{2+1}{2-1}=\cfrac{3}{1}=\bm{3}$

كما ترون، بمجرد تحليل كثيرات الحدود وتبسيطها، يصبح من السهل جدًا إيجاد الحل في النهاية.

عدم التحديد 0/0 مع الجذور

لقد رأينا للتو كيف يتم حل حالات عدم التحديد 0/0 للوظائف العقلانية. ومع ذلك، إذا كانت النهاية ذات دالة غير عقلانية (أو جذرية)، فسيتم حل عدم التحديد 0/0 بشكل مختلف.

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}$

أولاً، نحاول حل الحد عن طريق إجراء العمليات التالية:

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}=\frac{1-1}{\sqrt{1}-1}=\frac{0}{0}$

لكننا نحصل على صفر على صفر من عدم التحديد.

إذا كانت نهاية الدالة ذات الجذور تعطي عدم تحديد 0/0 ، فيجب عليك ضرب بسط ومقام الكسر في مرافق التعبير الجذري.

➤ تذكر أن المرافق هو نفس التعبير غير العقلاني ولكن مع تعديل الإشارة الوسطى.

بعد ذلك، نضرب كلًا من بسط الكسر ومقامه في مرافق التعبير الجذري:

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}$

ضمن هذا النوع من النهايات، من خلال القيام بهذه الخطوة، سنحصل دائمًا على متطابقة بارزة يمكننا تبسيطها. في هذه الحالة، في المقام لدينا حاصل ضرب المجموع والفرق، وبالتالي:

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}\right)^2-1^2}$

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{x-1}$

نقوم بتبسيط العامل المتكرر في البسط والمقام:

$\displaystyle\lim_{x \to 1} \frac{\cancel{\left(x-1\right)}\cdot\left(\sqrt{x}+1\right)}{\cancel{x-1}}=\lim_{x \to 1}\left(\sqrt{x}+1\right)$

وبهذه الطريقة يمكننا إيجاد نتيجة النهاية:

$\displaystyle\lim_{x \to 1}\left(\sqrt{x}+1\right)=\sqrt{1}+1=2$

تمارين محلولة على عدم التحديد 0/0

قمنا أدناه بإعداد العديد من التمارين التي تم حلها خطوة بخطوة حول حدود الدوال التي تعطي عدم تحديد 0/0. يمكنك محاولة القيام بها ثم التحقق من الحل.

لا تنس أنه يمكنك طرح أي أسئلة لديك حول حل الحدود في التعليقات!

التمرين 1

احسب نهاية الدالة الكسرية التالية عند النقطة x=-2.

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}$

انظر الحل

منطقيًا، نحاول أولاً حل النهاية:

$\displaystyle\lim_{x \to -2} \frac{x^2 +2x}{x^2-x-6}=\frac{(-2)^2+2\cdot (-2)}{(-2)^2-(-2)-6}=\frac{4-4}{4+2-6}=\frac{0}{0}$

لكن انتهى بنا الأمر مع عدم التحديد 0/0. لذلك يجب علينا تحليل كثيرات الحدود للبسط والمقام:

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}=\lim_{x \to -2}\frac{x(x+2)}{(x+2)(x-3)}$

نقوم الآن بتبسيط الكسر بإزالة الأقواس المتكررة في البسط والمقام:

$\displaystyle\lim_{x \to -2}\frac{x\cancel{(x+2)}}{\cancel{(x+2)}(x-3)}=\lim_{x \to -2}\frac{x}{x-3}$

وأخيرًا، نعيد حساب النهاية بالكسر المبسط:

$\displaystyle\lim_{x \to -2}\frac{x}{x-3}=\cfrac{-2}{-2-3}=\cfrac{-2}{-5}=\mathbf{\cfrac{2}{5}}$

تمرين 2

حل نهاية الدالة التالية عندما تقترب x من -1:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}$

انظر الحل

نحاول أولاً حل الحد كالمعتاد:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3-5(-1)^2+2(-1)+8} =\frac{0}{0}$

لكننا نحصل على عدم التحديد 0 بين 0. لذلك يجب علينا تحليل كثيرتي الحدود للكسر:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)(x-2)(x-4)}$

يمكننا الآن تبسيط كثيرات الحدود:

$\displaystyle\lim_{x \to -1}\frac{(x-1)\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x-2)(x-4)}=\lim_{x \to -1}\frac{(x-1)(x+2)}{(x-2)(x-4)}$

ونحل الحد:

$\displaystyle\lim_{x \to -1} \frac{(x-1)(x+2)}{(x-2)(x-4)}=\frac{ (-1-1)(-1+2)}{(-1-2)(-1-4)}=\frac{(-2)\cdot (1)}{(-3)\cdot (-5)}=\frac{\bm{-2}}{\bm{15}}$

التمرين 3

حدد حل نهاية الدالة الجذرية التالية:

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}$

انظر الحل

أولاً، نتحقق مما إذا كانت النهاية تعطي نوعًا من عدم التحديد:

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}=\frac{2^2-3\cdot2+2}{2-\sqrt{2\cdot 2}}=\frac{4-6+2}{2-2}=\frac{0}{0}$

النهاية تعطي عدم التعيين صفرًا مقسومًا على صفر، ولدينا جذر في الدالة. لذلك يجب علينا ضرب بسط الكسر ومقامه في مرافق التعبير الجذري:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{\left(2-\sqrt{2x}\right)\cdot \left(2+\sqrt{2x}\right)}$

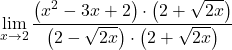
يتوافق المقام مع تطوير الهوية البارزة لمنتج المبلغ والفرق، وبالتالي يمكننا تبسيطه:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{2^2-\left(\sqrt{2x}\right)^2}$

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}$

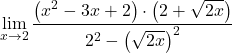
ومع ذلك، لا يمكننا بعد تبسيط حدود الكسر. لذلك يجب علينا تحليل كثيرات الحدود:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}=\lim_{x\to 2}\frac{(x-1)(x-2)\cdot\left(2+\sqrt{2x}\right)}{-2(x-2)}$

بهذه الطريقة يمكننا تبسيط الكسر:

$\displaystyle\lim_{x\to 2}\frac{(x-1)\cancel{(x-2)}\left(2+\sqrt{2x}\right)}{-2\cancel{(x-2)}}=\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}$

والآن يمكننا تحديد نتيجة الحد:

$\displaystyle\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}=\frac{(2-1)\left(2+\sqrt{2\cdot 2}\right)}{-2}=\frac{1\cdot (2+2)}{-2}=\bm{-2}$

التمرين 4

احسب النهاية عندما تقترب x من 0 للدالة الجذرية التالية:

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}$

انظر الحل

أولًا، نحاول حساب نهاية الدالة كما نفعل دائمًا:

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}=\frac{0+0}{3-\sqrt{4\cdot 0+9}}=\frac{0}{3-3}=\frac{0}{0}$

لكننا حصلنا على الصيغة غير المحددة 0/0. لذلك، نضرب بسط الدالة ومقامها في مرافق التعبير غير العقلاني:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{\left(3-\sqrt{4x+9}\right)\cdot\left(3+\sqrt{4x+9}\right)}$

نحن نطبق صيغة الهوية البارزة المقابلة لتبسيط المقام:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{3^2-\left(\sqrt{4x+9}\right)^2}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{9-(4x+9)}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

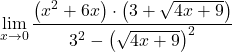
الآن نقوم بتحليل ذات الحدين من البسط عن طريق أخذ العامل المشترك:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

نقوم بتبسيط العوامل المتكررة في بسط ومقام الدالة:

$\displaystyle\lim_{x\to 0}\frac{\cancel{x}\left(x+6\right)\left(3+\sqrt{4x+9}\right)}{-4\cancel{x}}=\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}$

وأخيرًا، نحل نهاية الدالة:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}$

التمرين 5

حل النهاية التالية باستخدام طريقة عدم التحديد 0/0:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}$

➤ انظر: كيفية حساب الحدود الجانبية للدالة

انظر الحل

نحاول أولاً حل الحد:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3+5(-1)^2+7(-1)+3}=\frac{0}{0}$

لكن في النهاية نحصل على عدم تحديد صفر على صفر. ولذلك، فإننا نقوم بتحليل كثيرات الحدود في البسط والمقام:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)^2(x+3)}$

نقوم الآن بتبسيط الكسر من خلال حذف العوامل المتكررة في البسط والمقام:

$\displaystyle\lim_{x \to -1} \cfrac{(x-1)\cancel{(x+1)}(x+2)}{(x+1)^{\cancel{2}}(x+3)}=\lim_{x \to -1}\cfrac{(x-1)(x+2)}{(x+1)(x+3)}$

ونحسب الحد مرة أخرى:

$\displaystyle\lim_{x \to -1}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)(-1+2)}{(-1+1)(-1+3)}=\frac{-2\cdot 1}{0 \cdot 2}=\frac{-2}{0} =\infty$

لكننا الآن نجد أنفسنا أمام عدم تحديد رقم مقسوم على 0. لذلك يجب علينا حساب الحدود الجانبية للدالة عندما تميل x إلى -1.

نقوم أولاً بحل الحد الجانبي للدالة عند النقطة x=-1 على اليسار:

$\displaystyle\lim_{x \to -1^{-}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{-0}=+\infty$

ثم نحسب النهاية الجانبية للدالة عند النقطة x=-1 على اليمين:

$\displaystyle\lim_{x \to -1^{+}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{+0}=-\infty$

ولذلك، بما أن النهايتين الجانبيتين غير متطابقتين، فإن نهاية الدالة عند x=-1 غير موجودة:

$\displaystyle\displaystyle \lim_{x \to -1^-}f(x)= +\infty\neq\lim_{x \to -1^+}f(x)=-\infty\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to -1} f(x)$

كيفية حل عدم التحديد الصفري بين الصفر (0/0)

عدم التحديد 0/0 مع الجذور

تمارين محلولة على عدم التحديد 0/0

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد