▷ قاعدة السلسلة (المشتقات): تمارين محلولة

هنا سوف تتعلم ما هي قاعدة السلسلة وكيفية استخلاص الوظائف باستخدام قاعدة السلسلة. بالإضافة إلى ذلك، ستتمكن من رؤية العديد من الأمثلة على المشتقات التي تم حلها باستخدام قاعدة السلسلة، كما ستتمكن من التدرب على حل التمارين خطوة بخطوة على المشتقات التي تطبق قاعدة السلسلة.

ما هي قاعدة السلسلة؟

قاعدة السلسلة هي صيغة تستخدم لاشتقاق الدوال المركبة. تنص قاعدة السلسلة على أن مشتق الدالة المركبة f(g(x)) يساوي المشتق f'(g(x)) مضروبًا في المشتق g'(x) .

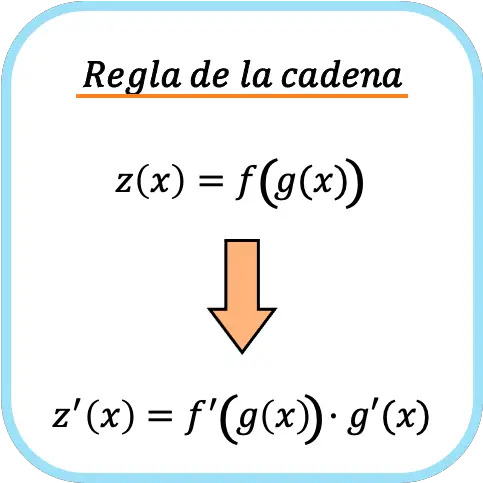
➤ انظر: الدالة المركبة

بشكل غير رسمي، غالبًا ما يُقال إن قاعدة السلسلة تهدف إلى التمييز بين الدالة ثم ضربها بما تحتوي عليه .

تتيح لنا صيغة قاعدة السلسلة التمييز بين الدوال المركبة بسهولة أكبر، لأننا إذا أردنا التمييز بين تركيبة من الدوال باستخدام حد التعريف المشتق، فسيتعين علينا إجراء الكثير من الحسابات.

ومن ناحية أخرى، يجب أن يؤخذ في الاعتبار أن هذه القاعدة تستخدم فقط للعثور على مشتقات الدوال المركبة، وليس من أي نوع من الدوال أو العمليات مع الدوال. على سبيل المثال، من الأخطاء الشائعة جدًا فهم الأمر بشكل خاطئ وتطبيق قاعدة السلسلة في المنتجات الوظيفية مثل ما يلي:

$\ln(x)\cdot x^2$

❌

لا يمكن استخدام قاعدة السلسلة إلا عندما يكون لدينا دالة داخل أخرى .

$\ln(x^2)$

✅

أمثلة على المشتقات مع قاعدة السلسلة

بالنظر إلى تعريف قاعدة السلسلة، سنشتق عدة وظائف باستخدام قاعدة السلسلة كمثال. تذكر أنه إذا لم تفهم في أحد الأمثلة كيفية اشتقاق الدالة باستخدام قاعدة السلسلة، فيمكنك أن تسألنا في التعليقات!

مثال 1

في هذا المثال، سوف نستخدم قاعدة السلسلة لاشتقاق اللوغاريتم الطبيعي لـ x تربيع:

$f(x)=\ln(x^2)$

مشتق اللوغاريتم الطبيعي يساوي 1 ضرب حجته، وبالتالي فإن المشتق

$f'\bigl(g(x)\bigr)$

يكون:

$f(x)=\ln(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{u}$

$f\bigl(g(x)\bigr)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\cfrac{1}{x^2}$

من ناحية أخرى، مشتقة x مرفوعة للقوة اثنين هي 2x:

$g(x)=x^2\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=2x$

وأخيرًا، نحسب مشتقة الدالة بأكملها من خلال تطبيق قاعدة السلسلة. مشتقة الدالة المركبة ستكون حاصل ضرب المشتقتين اللتين وجدناهما للتو:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x^2}\cdot 2x = \cfrac{2x}{x^2}=\cfrac{2}{x}$

مثال 2

في هذا المثال الثاني، سوف نشتق دالة محتملة بناءً على كثيرة الحدود:

$f(x)=\left(3x^2+4x-5\right)^3$

لاشتقاق قوة، علينا وضع الأس الأصلي أمامه وطرح وحدة واحدة من الأس، وبالتالي فإن مشتقة الدالة المحتملة دون تطبيق قاعدة السلسلة ستكون:

$f\bigl(g(x)\bigr)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=3\left(3x^2+4x-5\right)^2$

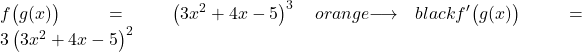
والآن نستنتج ما بين القوسين:

$g(x)=3x^2+4x-5\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=6x+4$

وأخيرًا، نستخدم قاعدة السلسلة لحل مشتقة الدالة بأكملها، والتي ستكون ضرب المشتقتين المحسوبتين سابقًا:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=3\left(3x^2+4x-5\right)^2\cdot (6x+4)$

مثال 3

في هذه الحالة، سنحل مشتقة الجيب لـ x تكعيب زائد 7x:

$f(x)=\text{sen}(x^3+7x)$

في الواقع، إنها تركيب دوال لأن لدينا الدالة x ³ +7x داخل دالة الجيب، وبالتالي يمكننا استخدام قاعدة السلسلة لإيجاد مشتقة الدالة المركبة.

من ناحية، مشتق الجيب هو جيب التمام، وبالتالي فإن مشتق الدالة الخارجية سيكون جيب التمام بنفس وسيطة الجيب:

$f\bigl(g(x)\bigr)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\text{cos}(x^3+7x)$

ومن ناحية أخرى، مشتقة x ³ +7x هي 3x ² +7.

$g(x)=x^3+7x\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=3x^2+7$

وبالتالي فإن مشتقة الدالة المركبة هي حاصل ضرب المشتقتين:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cos}(x^3+7x)\cdot (3x^2+7)$

حل تمارين على المشتقات باستخدام قاعدة السلسلة

التمرين 1

استنتج الدالة المركبة التالية باستخدام قاعدة السلسلة:

$f(x)=\left(5x^2-6x\right)^3$

انظر الحل

الدالة الخارجية هي دالة محتملة، لذا لحساب مشتقتها يجب عليك تطبيق الصيغة التالية:

$f\bigl(g(x)\bigr)=a\bigl(g(x)\bigr)^n \ \longrightarrow \ f'\bigl(g(x)\bigr)=n\cdot a\bigl(g(x)\bigr)^{n-1}$

$f\bigl(g(x)\bigr)=\left(5x^2-6x\right)^3\ \longrightarrow \ f'\bigl(g(x)\bigr)= 3\left(5x^2-6x\right)^2$

ثم نحسب مشتقة الدالة بالداخل. إنه طرح للقوى، لذا لحساب مشتقته يجب عليك تطبيق الصيغة التالية على كل حد من شروطه:

$f(x)=ax^n \ \longrightarrow \ f'(x)=n\cdot ax^{n-1}$

$g(x)=5x^2-6x\ \longrightarrow$

$g'(x)=2\cdot 5x^1-1 \cdot 6 x^0 =10x-6$

باختصار، مشتقة الدالة المركبة هي حاصل ضرب المشتقتين الموجودتين:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\left(5x^2-6x\right)^3 \ \longrightarrow \ \bm{f'(x)= 3\left(5x^2-6x\right)^2\cdot (10x-6)}$

تمرين 2

حل مشتقة الدالة المركبة التالية باستخدام قاعدة السلسلة:

$f(x)=-3\left(5x^5+9x^3\right)^4$

انظر الحل

أولا نوجد مشتقة الدالة الخارجية:

$\begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}$

والآن نحل مشتقة الدالة الداخلية:

$g(x)=5x^5+9x^3\ \longrightarrow \ g'(x)=25x^4+27x^2$

وبالتالي فإن مشتقة الدالة بأكملها هي:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=-3\left(5x^5+9x^3\right)^4 \ \longrightarrow \ \bm{f'(x)=-12\left(5x^5+9x^3\right)^3\cdot \left(25x^4+27x^2\right)}$

التمرين 3

احسب مشتقة تركيبة الدوال التالية باستخدام قاعدة السلسلة:

$f(x)=e^{2x^3}$

انظر الحل

إنها دالة أسية، لذا لحساب مشتقتها يجب عليك تطبيق الصيغة التالية:

$f(x)=e^{x} \ \longrightarrow \ f'(x)=e^{x}$

$f\bigl(g(x)\bigr)=e^{2x^3} \ \longrightarrow \ f'\bigl(g(x)\bigr)= e^{2x^3}$

نحن أيضًا نفرق الدالة عن أس الدالة:

$g(x)=2x^3 \ \longrightarrow \ g'(x)=6x^2$

ونستخدم قاعدة السلسلة لإيجاد مشتقة الدالة المركبة ذات العدد الصحيح:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=e^{2x^3} \ \longrightarrow \ \bm{f'(x)= e^{2x^3}\cdot 6x^2}$

التمرين 4

أوجد مشتقة الدالة المركبة التالية باستخدام قاعدة السلسلة:

$f(x)=\sqrt[3]{\text{sen}(x) +x }$

انظر الحل

هذا تركيب من الدوال، لأن لدينا دالة جيبية ودالة خطية في وسيطة دالة غير عقلانية. لذلك نحسب أولاً مشتق الجذر:

$f(x)=\sqrt[n]{x} \ \longrightarrow \ f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

$f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}$

والآن نستمد الحجة من الجذري. إنه مجموع الدوال، وبالتالي فإن المشتقة ستكون مجموع مشتقات كل حد:

$g(x)=\text{sen}(x) +x \ \longrightarrow \ g'(x)=\cos(x) + 1$

وبالتالي فإن مشتقة الدالة بأكملها تساوي ضرب المشتقتين المحسوبتين:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}$

التمرين 5

اشتق التركيب التالي للوظائف باستخدام قاعدة السلسلة:

$f(x)=3^{x^2+5}$

انظر الحل

لتطبيق قاعدة السلسلة، عليك إيجاد مشتقة القوة ومتعددة الحدود ثم ضربهما. وبالتالي، فإننا نستمد القوة باستخدام الصيغة المقابلة:

$f(x)=a^x \ \longrightarrow \ f'(x)=a^x\cdot \ln (a)$

$f\bigl(g(x)\bigr)=3^{x^2+5} \ \longrightarrow \ f'\bigl(g(x)\bigr)= 3^{x^2+5}\cdot \ln(3)$

ثانياً، نشتق الدالة كثيرة الحدود من الأس:

$g(x)=x^2+5 \ \longrightarrow \ g'(x)=2x$

وتخبرنا قاعدة السلسلة أن مشتقة الدالة بأكملها هي حاصل ضرب المشتقات التي وجدناها للتو:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=3^{x^2+5} \ \longrightarrow \ \bm{f'(x)= 3^{x^2+5}\cdot \ln(3) \cdot 2x}$

التمرين 6

$f(x)=\ln \bigl(4x^2 \cdot \cos(x) \bigr)$

انظر الحل

من الواضح أن الدالة في هذه المسألة مركبة، لأنه في جدال اللوغاريتم الطبيعي لدينا حاصل ضرب نوعين مختلفين من الدوال. لذلك نقوم أولاً بتمييز اللوغاريتم:

$f(x)=\ln(x) \ \longrightarrow \ f'(x)=\cfrac{1}{x}$

$f\bigl(g(x)\bigr)=\ln \bigl(4x^2 \cdot \cos(x) \bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{4x^2 \cdot \cos(x) }$

ثانيًا، نشتق الدالة من وسيطة اللوغاريتم. هذا ضرب لوظيفتين، لذلك يجب عليك استخدام الصيغة التالية للقيام بالاشتقاق:

$z(x)=f(x) \cdot g(x) \ \longrightarrow \ z'(x)=f'(x)\cdot g(x)+f(x) \cdot g'(x)$

$\begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}$

وبالتالي فإن مشتقة الدالة بأكملها، وفقًا لقاعدة السلسلة، ستكون حاصل ضرب المشتقتين:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}$

التمرين 7

حل مشتقة الدالة التالية باستخدام قاعدة السلسلة:

$f(x)=\log_9 (e^{x^2}-6x^7)$

انظر الحل

هذا تركيب من الدوال، لذا سنشتق اللوغاريتم ووسيطه بشكل منفصل ثم نضرب المشتقات.

لذا، أولًا، نقوم بتمييز اللوغاريتم للأساس 9:

$f(x)=\log_a (x) \ \longrightarrow \ f'(x)=\cfrac{1}{x\cdot \ln (a)}$

$f\bigl(g(x)\bigr)=\log_9 (e^{x^2}-6x^7) \ \longrightarrow \ f'\bigl(g(x)\bigr)=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}$

والآن نحسب مشتقة سعة اللوغاريتم. لاحظ أن الرقم e له دالة في وسيطته، أي أنها دالة مركبة، لذلك نحتاج أيضًا إلى تطبيق قاعدة السلسلة لاشتقاق هذه الدالة:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$h(x)=e^{x^2} \ \longrightarrow \ h'(x)=e^{x^2}\cdot \bigl(x^2\bigr)' =e^{x^2}\cdot 2x$

وبالتالي، فإن مشتقة الوسيطة الصحيحة للوغاريتم ستكون:

$g(x)= e^{x^2}-6x^7\ \longrightarrow \ g'(x)=e^{x^2}\cdot 2x - 42x^6$

وأخيرًا، مشتقة الدالة بأكملها ستكون حاصل ضرب f'(g(x)) وg'(x):

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}$

التمرين 8

استنتج الدالة المركبة التالية باستخدام قاعدة السلسلة:

$f(x)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)$

انظر الحل

في هذا التمرين، لدينا تركيبة من عدة وظائف، لذا سيتعين علينا تطبيق قاعدة السلسلة عدة مرات. نشتق أولاً الدالة المثلثية من الجيب، ومشتقته هي جيب التمام:

$f\bigl(g(x)\bigr)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)\ \longrightarrow \ f'\bigl(g(x)\bigr)=\cos\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)$

والآن نحسب مشتقة وسيطة الجيب باستخدام قاعدة السلسلة:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}$

وأخيرًا، نحصل على مشتقة التركيبة الكاملة للدوال من خلال تطبيق قاعدة السلسلة مرة أخرى:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\bm{f'(x)=\cos } \bm{\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr) \cdot 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-}\mathbf{sen}\bm{(x)\Bigr)}$

إثبات قاعدة السلسلة

وأخيرًا، سنثبت صيغة قاعدة السلسلة. للقيام بذلك، سنبدأ من التعريف الرياضي للمشتق:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

لتكن z دالة مكونة من وظيفتين:

$z=f\bigl(g(x)\bigr)$

إذن مشتق الدالة z الذي يطبق التعريف سيكون:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}$

كما تعلم، يمكنك ضرب وقسمة كسر على نفس الحد، لأن هذا لا يغير النتيجة. لذلك يمكننا الانتقال إلى الخطوة التالية:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}\cdot \frac{g(x+h)-g(x)}{g(x+h)-g(x)}$

نعيد ترتيب مقامات الكسور:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \frac{g(x+h)-g(x)}{h}$

ومن خلال تطبيق خصائص النهايات، يمكننا تقسيم النهاية المذكورة أعلاه إلى قسمين. بما أن نهاية المنتج تساوي منتج الحدود:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

وهذا التعبير يعادل ما يلي:

$\displaystyle z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

وبذلك تكون صيغة قاعدة السلسلة مثبتة، إذ وصلنا إليها من تعريف المشتقة.

ما هي قاعدة السلسلة؟

أمثلة على المشتقات مع قاعدة السلسلة

مثال 1

مثال 2

مثال 3

حل تمارين على المشتقات باستخدام قاعدة السلسلة

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

التمرين 7

التمرين 8

إثبات قاعدة السلسلة

اترك تعليقاً إلغاء الرد