الزاوية بين خطين (صيغة)

ستجد في هذه الصفحة شرح كيفية حساب الزاوية بين خطين (الصيغة). ستتمكن أيضًا من رؤية العديد من الأمثلة، بالإضافة إلى ذلك، ستتمكن من التدرب على التمارين التي تم حلها خطوة بخطوة.

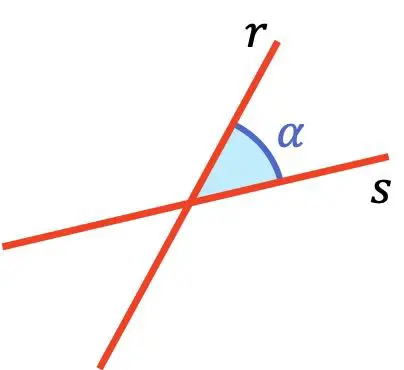
ما هي الزاوية بين خطين؟

الزاوية المحصورة بين خطين هي أصغر زاوية بين هذين الخطين.

يوجد في المخطط أربعة أنواع من الخطوط حسب الزاوية التي تشكلها بينها: الخطوط المتقاطعة (بين 0 درجة و 90 درجة)، والخطوط المتعامدة (90 درجة)، والخطوط المتوازية (0 درجة)، والخطوط المتوازية (0 درجة).

خطوط متقاطعة

تتقاطع الخطوط المتقاطعة بزاوية حادة بين 0 درجة و 90 درجة.

خطوط مستقيمة متعامدة

تتقاطع الخطوط المتعامدة بزاوية قائمة قدرها 90 درجة.

خطوط متوازية

الخطوط المتوازية لا تتلامس أبدًا وتكون بينهما زاوية مقدارها 0 درجة.

خطوط متطابقة

هناك خطان متطابقان تشتركان في جميع نقاطهما، وبالتالي هناك دائمًا زاوية مقدارها 0 درجة بينهما.

وفي الختام، فإن حساب الزاوية بين خطين متوازيين أو متوازيين أو متعامدين يكون فوريًا: فالخطوط المتوازية والخطوط المتوازية تشكل زاوية مقدارها 0 درجة حيث أن لهما نفس الاتجاه، ويتقاطع الخطان المتعامدان بزاوية 90 درجة . من ناحية أخرى، للعثور على الزاوية بين خطين متقاطعين، يجب عليك تطبيق صيغة (سنرى ذلك أدناه).

كيف يتم حساب الزاوية بين خطين؟

هناك طريقتان لحساب الزاوية بين خطين. تستخدم الطريقة الأولى متجه الاتجاه لكل خط، وتعتمد الطريقة الثانية على ميل كل خط.

لا يوجد أي إجراء أفضل من الآخر، في الواقع كلاهما سهل للغاية، ولكن اعتمادًا على كيفية التعبير عن الخطوط بطريقة أو بأخرى يعد أمرًا عمليًا. لذلك ننصحك بمعرفة كيفية استخدام كلا الطريقتين الرياضيتين.

طريقة توجيه الخط المتجه

صيغة حساب الزاوية بين خطين باستخدام متجهات اتجاههما هي:

بالنظر إلى متجهات الاتجاه لخطين مختلفين:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

يمكن حساب الزاوية بين هذين الخطين بالصيغة التالية:

$\displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

ذهب

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

هي وحدات من المتجهات

$\vv{\text{u}}$

$\vv{\text{v}}$

على التوالى.

تذكر أن صيغة حجم المتجه هي:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

دعونا نرى كيفية العثور على الزاوية بين خطين مع مثال:

احسب الزاوية المحصورة بين الخطين التاليين:

$\displaystyle r: \ \begin{cases} x=2-3t \\[2ex]y=1+4t \end{cases} \qquad s: \ 2x-5y+7=0$

لحساب الزاوية بين الخطين، عليك أولاً العثور على متجه الاتجاه لكل خط.

الحق

$r$

يتم التعبير عنها في شكل معادلة بارامترية ، وبالتالي فإن مكونات المتجه الذي يحدد اتجاهه هي:

$\vv{r} = (-3,4)$

والقانون

$\displaystyle s$

يتم تعريفه في شكل معادلة ضمنية (أو عامة)، وبالتالي فإن إحداثيات متجه اتجاهه هي:

$\vv{s} = (-B,A)$

$\vv{s} = (5,2)$

الآن بعد أن عرفنا متجه الاتجاه لكل خط، يمكننا استخدام صيغة الزاوية بين خطين:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

لذلك نحدد حجم المتجهين:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-3)^2+4^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{5^2+2^2}= \sqrt{29}$

نقوم بإجراء العمليات المتجهة لصيغة الزاوية:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-3,4) \cdot (5,2)\rvert}{5 \cdot \sqrt{29}}= \cfrac{\lvert-3 \cdot 5 + 4\cdot 2\rvert}{26,93} = \cfrac{7}{26,93} = 0,26$

وأخيرًا، نحسب الزاوية التي يشكلها الخطان مع معكوس جيب التمام:

$\alpha= \text{cos}^{-1}(0,26) = \bm{74,93º}$

تذكر أنه يمكنك حساب معكوس جيب التمام باستخدام الآلة الحاسبة باستخدام المفتاح

$\boxed{\cos ^{-1}}.$

طريقة المنحدر

من الواضح، لفهم هذه الطريقة، عليك أن تعرف ميل الخط . يمكنكم مراجعة هذا المفهوم في الرابط حيث تجدون شرحا مفصلا عن معناه وكيفية حسابه وأمثلة وتمارين محلولة لميل الخط المستقيم.

صيغة حساب الزاوية بين خطين من ميليهما هي:

أو خطين متميزين:

$r_1 : \ y=m_1 x+n_1 \qquad r_2: \ y=m_2 x+n_2$

يمكن تحديد الزاوية بين هذين الخطين بالصيغة التالية:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

ذهب

$m_1$

$m_2$

هي منحدرات الخطوط

$r_1$

$r_2$

على التوالى.

دعونا نرى كيفية حساب الزاوية بين خطين باستخدام ميلهما مع مثال:

أوجد الزاوية المحصورة بين الخطين التاليين:

$\displaystyle r: \ y=4x-2 \qquad s: \ y=-3x+1$

ميل كل سطر هو الرقم الموجود قبل المتغير

$x:$

$m_r = 4$

$m_s = -3$

ولذلك، يمكن العثور على الزاوية بين الخطين من خلال تطبيق صيغة الميل:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-3-4}{1+4\cdot (-3)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-11} \end{vmatrix} = 0,64$

وأخيرًا نجد الزاوية مع معكوس المماس:

$\alpha= \text{tg}^{-1}(0,64) = \bm{32,62º}$

تذكر أنه يمكنك حساب معكوس المماس باستخدام الآلة الحاسبة باستخدام المفتاح

$\boxed{\tan ^{-1}}.$

لقد رأينا للتو مثالًا يوضح ميلي خطين معبرًا عنهما بمعادلة صريحة، لكن إذا كانا في صورة معادلة ميل ونقطة، فيجب استخدام نفس الإجراء.

حل مسائل الزوايا بين خطين

التمرين 1

حدد الزاوية المتكونة من الخطين التاليين:

$\displaystyle r: \ \begin{cases} x=4+t \\[2ex]y=-3-2t \end{cases} \qquad s: \ \begin{cases} x=4t \\[2ex]y=-1-t \end{cases}$

انظر الحل

في هذه الحالة، سوف نستخدم طريقة متجه الاتجاه. ولذلك، علينا أولًا إيجاد متجه الاتجاه لكل خط. يتم التعبير عن كلا الخطين كمعادلات بارامترية، وبالتالي فإن مكونات متجهات اتجاههما هي الحدود الموجودة أمام المعلمة

$t:$

$\vv{r} = (1,-2)$

$\vv{s} = (4,-1)$

الآن بعد أن عرفنا متجه الاتجاه لكل خط، يمكننا استخدام صيغة الزاوية بين خطين:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

لذلك نحدد حجم المتجهين:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{1^2+(-2)^2}= \sqrt{5}$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

نحل المنتج القياسي بين متجهي البسط وضرب وحدات المقام:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(1,-2) \cdot (4,-1)\rvert}{\sqrt{5} \cdot \sqrt{17}}= \cfrac{\lvert 1 \cdot 4 + (-2)\cdot (-1)\rvert}{9,22} = \cfrac{6}{9,22} = 0,65$

وأخيرًا، نجد الزاوية المتكونة من الخطين عن طريق إجراء معكوس جيب التمام:

$\alpha= \text{cos}^{-1}(0,65) = \bm{49,40º}$

تمرين 2

أوجد الزاوية المحصورة بين الخطين التاليين:

$\displaystyle r: \ -3x+4y+1=0 \qquad s: \ \cfrac{x-1}{6} = \cfrac{y+5}{3}$

انظر الحل

سنحل هذه المشكلة باستخدام طريقة متجه الاتجاه، لذا علينا أولًا إيجاد متجه الاتجاه لكل خط. الحق

$r$

يتم التعبير عنها في شكل معادلة عامة (أو ضمنية)، بحيث تكون مكونات المتجه الذي يحدد اتجاهه هي:

$\vv{r} = (-B,A)$

$\vv{r} = (-4,-3)$

والقانون

$\displaystyle s$

يتم تعريفه في شكل معادلة مستمرة، وبالتالي فإن الإحداثيات الديكارتية لمتجه اتجاهه هي أرقام المقامات:

$\vv{s} = (6,3)$

بمجرد أن نعرف متجه الاتجاه لكل خط، يمكننا استخدام صيغة الزاوية بين خطين:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

لذلك نحدد وحدات المتجهين:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-4)^2+(-3)^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{6^2+3^2}= \sqrt{45}$

نقوم بتنفيذ العمليات بين متجهات صيغة الزاوية:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-4,-3) \cdot (6,3)\rvert}{5 \cdot \sqrt{45}}= \cfrac{\lvert -4 \cdot 6 + (-3)\cdot 3\rvert}{33,54} = \cfrac{33}{33,54} = 0,98$

وأخيرًا، نحسب الزاوية التي يشكلها الخطان مع معكوس جيب التمام:

$\alpha= \text{cos}^{-1}(0,98) = \bm{10,30º}$

التمرين 3

ما هي الزاوية المحصورة بين الخطين التاليين؟

$\displaystyle r: \ y=-2x+9 \qquad s: \ y=5x-1$

انظر الحل

في هذه الحالة سنستخدم طريقة ميل الخطوط لمعرفة الزاوية التي تصنعها، حيث أن الخطوط على شكل معادلة صريحة.

ميل كل سطر هو الرقم المصاحب للمتغير المستقل

$x:$

$m_r = -2$

$m_s = 5$

ولذلك، يمكن تحديد الزاوية بين الخطين من خلال تطبيق صيغة الميل:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-2-5}{1+5\cdot (-2)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-9} \end{vmatrix} = 0,78$

وأخيرًا نجد الزاوية المحصورة بين الخطين عن طريق عكس الظل:

$\alpha= \text{tg}^{-1}(0,78) = \bm{37,87º}$

التمرين 4

أوجد معادلة الخط الذي يمر بالنقطة

$P(5,-1)$

ويشكل زاوية 45 درجة مع الخط

$r.$

يقال الخط:

$\displaystyle r: \ y=2x+4$

انظر الحل

لحل المشكلة سوف نتصل

$s$

إلى اليمين الذي سنقوم بحسابه. بالإضافة إلى ذلك، سوف نستخدم طريقة الميل لأننا نعرف ميل الخط المستقيم

$r:$

$m_r=2$

من صيغة الزاوية بين خطين (طريقة الميل) يمكننا الحصول على قيمة ميل الخط

$s:$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

نستبدل القيم المعروفة في الصيغة:

$\displaystyle \text{tg}(45º) =\begin{vmatrix} \cfrac{m_s-2}{1+2\cdot m_s} \end{vmatrix}$

ونحاول حل المعادلة الناتجة:

$\displaystyle 1 =\begin{vmatrix} \cfrac{m_s-2}{1+2m_s} \end{vmatrix}$

القيمة المطلقة للمعادلة تجعل حلها صعبًا إلى حد ما، لأنه يتعين عليك تحليل كلا الخيارين الموجب والسالب:

$\displaystyle 1 =+\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=m_s-2$

$\displaystyle 1+2m_s=m_s-2$

$\displaystyle 2m_s-m_s=-2-1$

$\displaystyle m_s=-3$

$\displaystyle 1 =-\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=-(m_s-2)$

$\displaystyle 1+2m_s=-m_s+2$

$\displaystyle 2m_s+m_s=2-1$

$\displaystyle 3m_s=1$

$\displaystyle m_s=\cfrac{1}{3}$

وبالتالي، لدينا حلان محتملان: خط ميله -3 وخط آخر ميله ثلث.

صيغة معادلة نقطة الميل للخط هي:

$y-y_0=m(x-x_0)$

ولذلك، بمجرد أن نعرف ميل الخطين المحتملين، يمكننا أن نكتب معادلة نقطة الميل لكل خط مع النقطة التي يجب أن يمر من خلالها وفقا للعبارة،

$P(5,-1):$

$\displaystyle s: \ y+1=-3(x-5) \qquad \qquad s': \ y+1=\cfrac{1}{3}(x-5)$

ما هي الزاوية بين خطين؟

كيف يتم حساب الزاوية بين خطين؟

طريقة توجيه الخط المتجه

طريقة المنحدر

حل مسائل الزوايا بين خطين

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد