نشرح في هذه المقالة كيفية معرفة رتابة الدالة، أي كيفية العثور على فترات الزيادة والنقصان للدالة. بالإضافة إلى ذلك، يمكنك التدرب من خلال تمارين خطوة بخطوة حول نمو الوظيفة وتراجعها.
ما هي رتابة وظيفة؟
تكون الدالة رتيبة في الفترة إذا حافظت على الترتيب المعطى. هناك خمسة أنواع من الرتابة:
- دالة متزايدة بشكل رتيب: عندما تكون قيمة الدالة عند نقطة ما مساوية أو أكبر من قيمة الدالة عند نقطة سابقة.
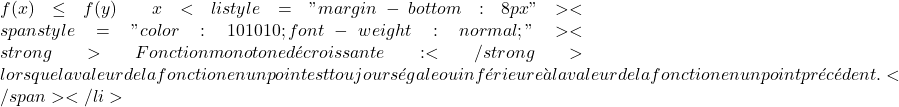دالة متزايدة بشكل رتيب: عندما تكون قيمة الدالة عند نقطة ما أكبر دائمًا من قيمة الدالة عند نقطة سابقة.
دالة ثابتة عندما تكون قيمة الدالة عند نقطة ما مساوية دائمًا لقيمة الدالة عند نقطة سابقة.
x^2-4=0x^2=4x=\pm 2
\text{Dom } f= \mathbb{R}-\{+2, -2 \}
f(x)=\cfrac{3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-4) – 3\cdot 2x}{\left( x^2-4\يمين)^2}f'(x)=\cfrac{-6x}{\left(x^2-4\يمين)^2}
f'(x)=0\cfrac{-6x}{\left(x^2-4\right)^2}=0
\يسار(x^2-4\يمين)^2}
-6x=0\cdot \left(x^2-4\right)^2-6x=0x=\cfrac{0}{-6}x=0
و'(س)=0,
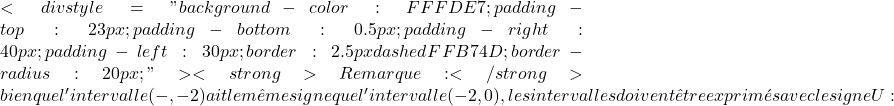
(-\infty,0)
و'(س)=0.
f(x)=x^3-6x^2+9x \ \longrightarrow \ f'(x)=3x^2-12x+9
f'(x)= 03x^2-12x+9=0\begin{align}x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} = \cfrac{-(- 12) \pm \sqrt{(-12)^2-4\cdot 3 \cdot 9}}{2\cdot 3}=\\[2ex]&= \cfrac{+12 \pm \sqrt{144-108 }}{6} =\cfrac{12 \pm 6}{6}=\begin{الحالات} \cfrac{12 + 6}{6}= 3 \\[4ex] \cfrac{12 – 6}{6} =1 \end{الحالات} \end{محاذاة}
و'(س)=0
\text{Dom } f= \mathbb{R}-\{+3, -3 \}
f(x)=\cfrac{5}{x^2-9} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-9) – 5\cdot (2x)}{\ left(x^2-9\right)^2}f'(x)= \cfrac{-10x}{\left(x^2-9\right)^2}
f'(x)= 0\cfrac{-10x}{\left(x^2-9\right)^2}=0 -10x=0\cdot \left(x^2-9\right)^2 – 10x= 0 x= \cfrac{0}{-10} x=0
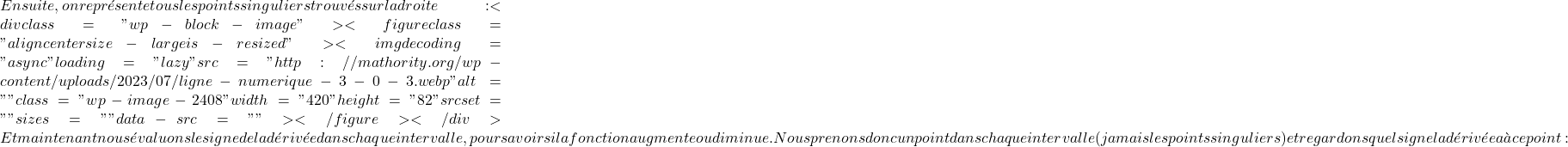
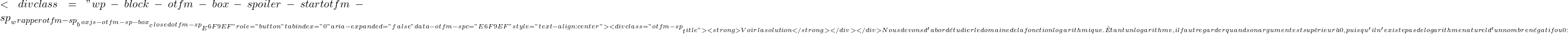
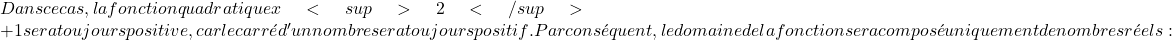
f(x)=\ln \bigl(x^2+1 \bigr) \ \longrightarrow \ f'(x)=\cfrac{1}{x^2+1 } \cdot (2x)f'(x) = \cfrac{2x}{x^2+1}
f'(x)= 0\cfrac{2x}{x^2+1}=0 2x=0\cdot \left(x^2+1\right) 2x= 0 x= \cfrac{0}{2} س = 0
