دالة الجيب الزائدية

ستجد في هذه المقالة كل شيء عن جيب الزاوية الزائدي: ما هي صيغته، تمثيله البياني، جميع خصائصه، العلاقات مع الدوال الأخرى،…

صيغة الجيب الزائدية

دالة الجيب الزائدية هي إحدى الدوال القطعية الرئيسية ويتم تمثيلها بالرمز sinh(x) أو sinh(x) . الجيب الزائدي يساوي e ^x ناقص e ^-x مقسومًا على 2.

وبالتالي فإن صيغة الجيب الزائدي هي كما يلي:

$\displaystyle\text{senh}(x)=\cfrac{e^{x}-e^{-x}}{2}$

وبالتالي، فإن الجيب الزائدي يرتبط بالدالة الأسية.

➤ انظر: خصائص الدالة الأسية

تمثيل رسومي للجيب الزائدي

باستخدام الصيغة التي رأيناها في القسم السابق، يمكننا إنشاء جدول لقيم الجيب الزائدية ورسم الدالة رسمًا بيانيًا:

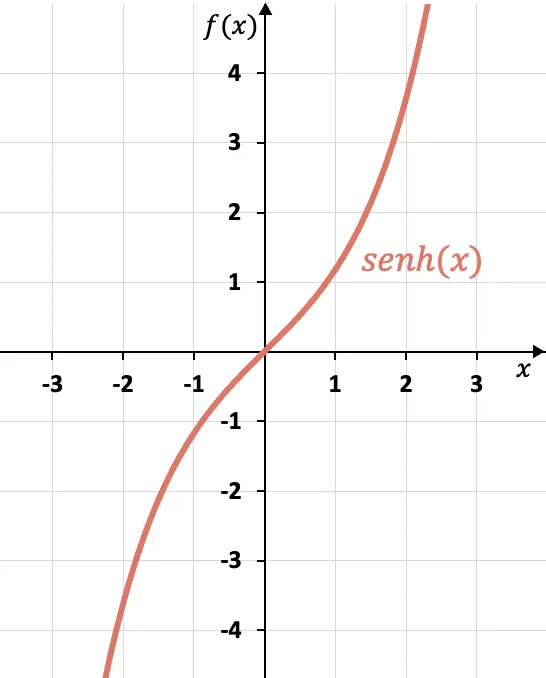
في هذا الرسم البياني، يمكننا أن نرى أن الجيب الزائدي هو دالة فردية ، لأن x المعاكس له صور متقابلة، أو بمعنى آخر، الرسم البياني الجيبي الزائدي متماثل حول أصل الإحداثيات (0، 0).

كما ترون، فإن الرسم البياني للجيب الزائدي يختلف تمامًا عن الرسم البياني للجيب، وهي دالة دورية. يمكنك مشاهدة التمثيل الرسومي للجيب وجميع الاختلافات مع الجيب الزائدي في الرابط التالي:

➤ انظر:التمثيل الرسومي لدالة الجيب

خصائص الجيب الزائدي

الجيب الزائدي له الخصائص التالية:

مجال دالة الجيب الزائدية هو كل الأعداد الحقيقية:

$\text{Dom } f = \mathbb{R}$

نطاق أو نطاق دالة الجيب الزائدية كلها أرقام حقيقية أيضًا.

$\text{Im } f= \mathbb{R}$

الجيب الزائدي هو دالة مستمرة وغريبة.

$\displaystyle \text{senh}(-x) =- \text{senh}(x)$

يتقاطع المحور X والمحور Y عند نفس نقطة التقاطع، أصل الإحداثيات:

$(0,0)$

حد دالة الجيب الزائدية عندما تميل x إلى زائد/ناقص ما لا نهاية يساوي زائد/ناقص ما لا نهاية:

$\displaystyle\lim_{x\to+\infty}\text{senh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{senh}(x)=-\infty$

يتزايد جيب القطع الزائد بشكل صارم في جميع أنحاء المجال، لذلك ليس له الحد الأقصى أو الحد الأدنى.

ومع ذلك، فإنه يغير انحناءه عند النقطة x = 0، لذلك فهو نقطة انقلاب للدالة. بالنسبة للقيم الأقل من x=0 فهي دالة مقعرة، من ناحية أخرى للقيم الأكبر من x=0 فهي دالة محدبة.

مشتق دالة الجيب الزائدية هو جيب التمام الزائدي:

$f(x)=\text{senh}(x) \ \longrightarrow \ f'(x)=\text{cosh}(x)$

وبالمثل، فإن تكامل دالة الجيب الزائدية هو جيب التمام الزائدي:

$\displaystyle \int \text{senh}(x) \ dx= \text{cosh}(x) + C$

سلسلة تايلور لدالة الجيب الزائدية تعادل التعبير التالي:

$\displaystyle\text{senh}(x)=x+\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\cfrac{x^7}{7!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n+1}}{(2n+1)!}$

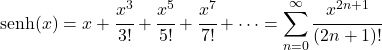
تحويل لابلاس لدالة الجيب الزائدية هو كما يلي:

$\mathcal{L}\bigl[\text{senh}(at)\bigr]=\cfrac{a}{s^2-a^2}$

العلاقات الرياضية للجيب الزائدي

يرتبط جيب القطع الزائد بالدوال القطعية الأخرى من خلال المعادلات التالية:

المعادلة الأساسية تربط جيب التمام الزائدي بجيب التمام الزائدي:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

لذلك، ترتبط دوال الجيب وجيب التمام الزائدية بمعادلة القطع الزائد، وهي x ² -y ² =1. على عكس دوال الجيب وجيب التمام المثلثية المرتبطة بمعادلة الدائرة (x ² +y ² =1).

يمكن ربط الدوال الزائدية للجيب وجيب التمام والظل بالمعادلة التالية:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$