دالة التناسب العكسي

تشرح هذه الصفحة ماهية دوال التناسب العكسي وكيفية رسمها بيانيًا. بالإضافة إلى ذلك، ستجد جميع خصائص هذا النوع من الوظائف، وكيفية حساب مجالها، بالإضافة إلى العديد من الأمثلة والتمارين التي تم حلها خطوة بخطوة للتمرين.

ما هي وظيفة التناسب العكسي؟

وبالتالي، فإن دوال التناسب العكسي تتكون دائمًا من كسور ذات حدود متعددة الحدود من الدرجة الأولى في المقام. ولذلك، فهي نوع من وظيفة عقلانية.

أمثلة على وظائف التناسب العكسي:

عمومًا

هو عموما المتغير المستقل و

المتغير التابع، أو بمعنى آخر المتغير

يعتمد على

من ناحية أخرى، يمكن أن تكون نسبة التناسب (مصطلح البسط) موجبة أو سالبة وإشارتها تشير إلى زيادة أو نقصان الدالة:

• إذا كان ثابتا

  

  سالبة، الدالة آخذة في الازدياد.

• بدلا من ذلك، إذا كان الثابت

  

  إيجابية، الدالة آخذة في التناقص.

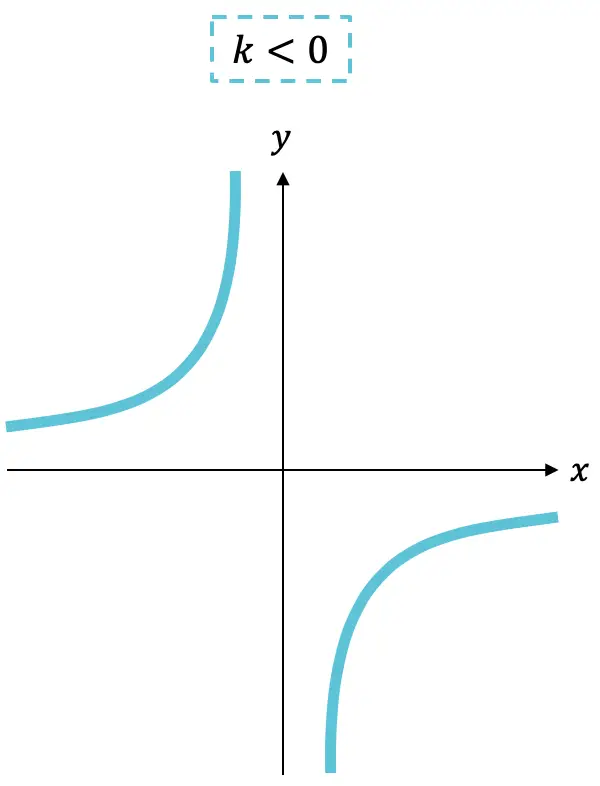
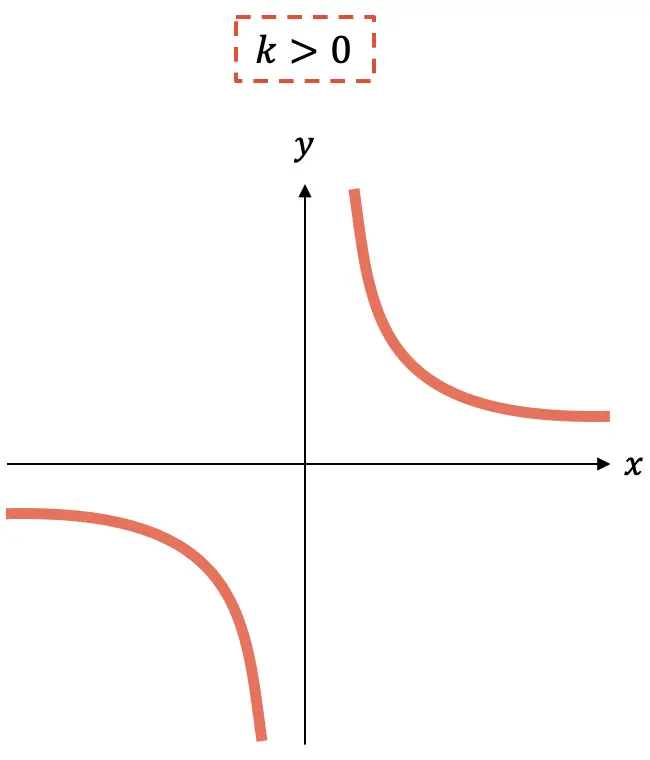
كما ترون، الرسم البياني لدالة التناسب العكسي يتكون دائمًا من قطعتين زائدتين ، اعتمادًا على إشارة k ، ستكونان في ربع واحد أو آخر.

مجال دالة التناسب العكسي

كونها نوعًا من الدالة الكسرية، فإن مجال دالة التناسب العكسي هو جميع الأعداد الحقيقية باستثناء تلك التي تختفي من المقام . لأن المقام لا يمكن أن يكون صفرًا أبدًا، لأن ذلك سيؤدي إلى ما لا نهاية.

على سبيل المثال، سوف نحدد مجال دالة التناسب العكسي التالية:

لمعرفة متى يكون المقام صفرًا، يجب علينا مساواة تعبيره بالصفر وحل المعادلة:

وبالتالي، عندما تأخذ x القيمة 1، سيكون المقام صفرًا وسنحصل على عدم التحديد. إذن، مجال الدالة هو كل الأعداد الحقيقية ناقصًا

كيفية رسم دالة التناسب العكسي

سنرى كيفية رسم دالة التناسب العكسي باستخدام مثال.

• سنمثل الوظيفة التالية في الرسم البياني:

أول ما علينا فعله هو إيجاد مجال الدالة. كونه كسرًا، لا يمكن أن يكون المقام صفرًا أبدًا، لأن ذلك سيؤدي إلى ما لا نهاية. ولذلك، فإن المجال سيكون كله x إلا عندما يتم إلغاء المقام.

لذلك، قمنا بتعيين المقام يساوي 0 لمعرفة x الذي لا ينتمي إلى المجال:

وبالتالي فإن مجال الدالة هو جميع الأرقام باستثناء 2:

بمجرد أن نعرف الرقم الذي لا ينتمي إلى المجال، نقوم بإنشاء جدول القيم. لتمثيل وظائف التناسب العكسي، من الضروري حساب 3 أو 4 نقاط إلى اليسار و3 أو 4 نقاط إلى يمين الرقم الذي لا ينتمي إلى المجال (2):

الآن لنمثل النقاط على الرسم البياني :

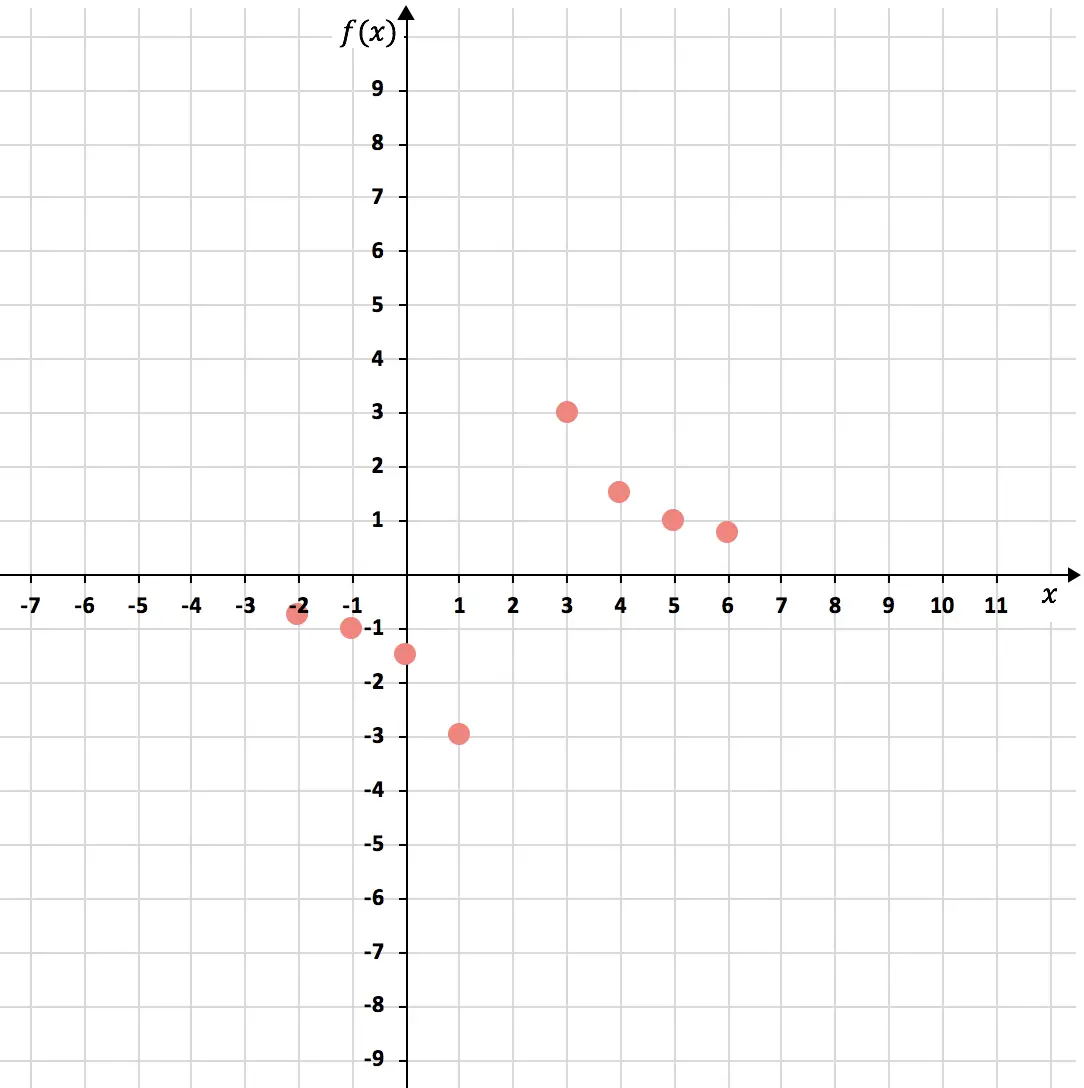
وأخيرًا، نربط النقاط لتكوين القطع الزائد في دالة التناسب العكسي. بالإضافة إلى ذلك، نقوم بإطالة فروع القطع الزائدة للإشارة إلى أنها مستمرة في النمو:

لاحظ أن الدالة تقريبية

، سواء على اليمين أو على اليسار. ومع ذلك، فهو لا يصل إلى 2 أبدًا، فهو يقترب جدًا ولكنه لا يصل إليه أبدًا. لذا،

وهو الخط المقارب العمودي . انه بسبب

لا تنتمي إلى مجال الدالة، وبالتالي فإن الدالة غير موجودة عند هذه النقطة.

ويحدث نفس الشيء مع المحور X الأفقي. الدالة تقريبية

ولكن لا تلمسها أبدًا. حتى الآن،

هو الخط المقارب الأفقي .

وهذا يعني أن جميع دوال التناسب العكسي متقطعة، لأنها تحتوي دائمًا على خط مقارب.

يمكنك معرفة المزيد عن الخطوط المقاربة وحدود الدوال على موقعنا.

حل مشاكل وظائف التناسب العكسي

التمرين 1

احسب مجال دالة التناسب العكسي التالية:

لن توجد دالة التناسب العكسي عندما يكون المقام 0، لأن الدالة عندها ستعطي ∞. لذلك، نحتاج إلى جعل مقام الدالة يساوي 0 لنرى أن x يلغي المقام، وبالتالي لا ينتمي إلى المجال.

تمرين 2

ارسم دالة التناسب العكسي التالية:

أول شيء يجب فعله هو حساب مجال الدالة:

بمجرد أن نعرف الرقم الذي لا ينتمي إلى المجال، نقوم بإنشاء مصفوفة من القيم باستخدام الدالة:

أخيرًا، نمثل النقاط التي تم الحصول عليها على الرسم البياني ونرسم القطع الزائدة، وبالتالي نشكل دالة التناسب العكسي:

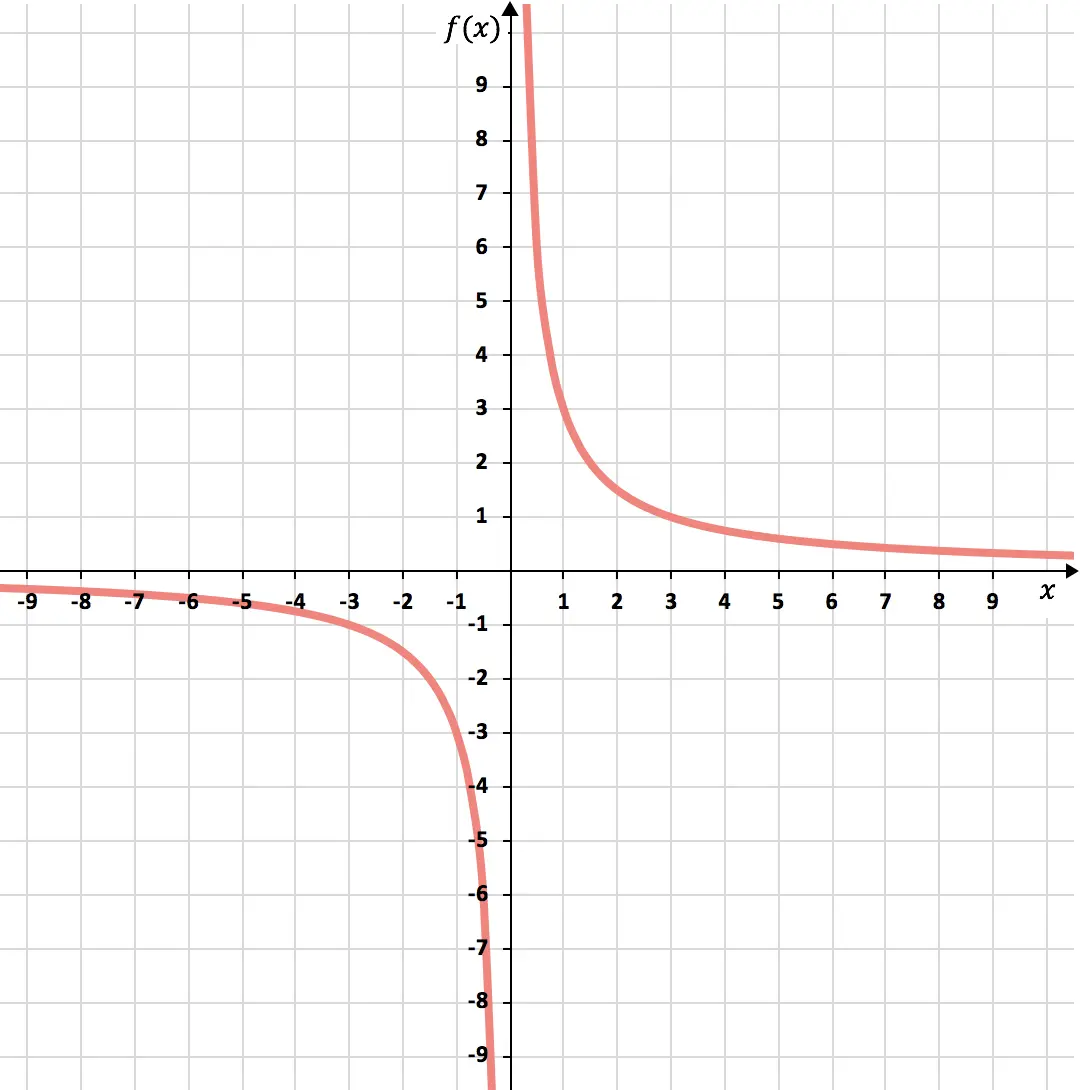
التمرين 3

ارسم دالة التناسب العكسي التالية:

أول شيء يجب فعله هو حساب مجال الدالة:

بمجرد أن نعرف مجال الدالة، نقوم بإنشاء جدول القيم:

أخيرًا، نمثل النقاط التي تم الحصول عليها على الرسم البياني ونرسم القطع الزائدة، وبالتالي نشكل دالة التناسب العكسي:

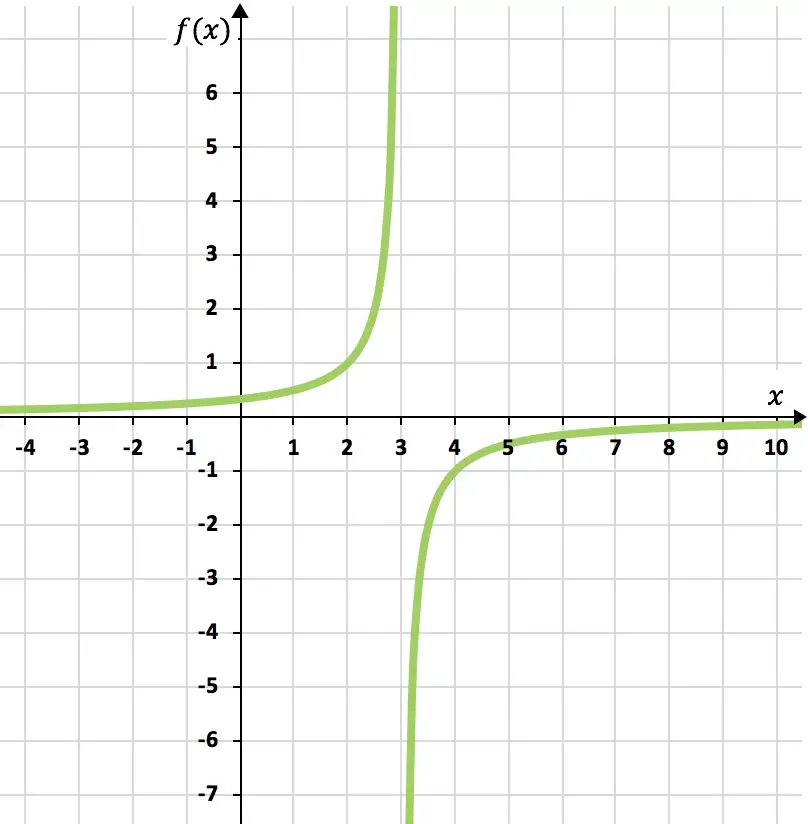
التمرين 4

ارسم دالة التناسب العكسي التالية:

أولا، علينا حساب مجال الدالة:

بمجرد أن نعرف مجال الدالة، نقوم بإنشاء مجموعة من القيم:

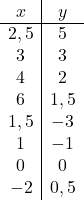
وأخيرًا، نمثل النقاط التي تم الحصول عليها على الرسم البياني ونرسم القطع الزائد، وبالتالي نشكل دالة التناسب العكسي:

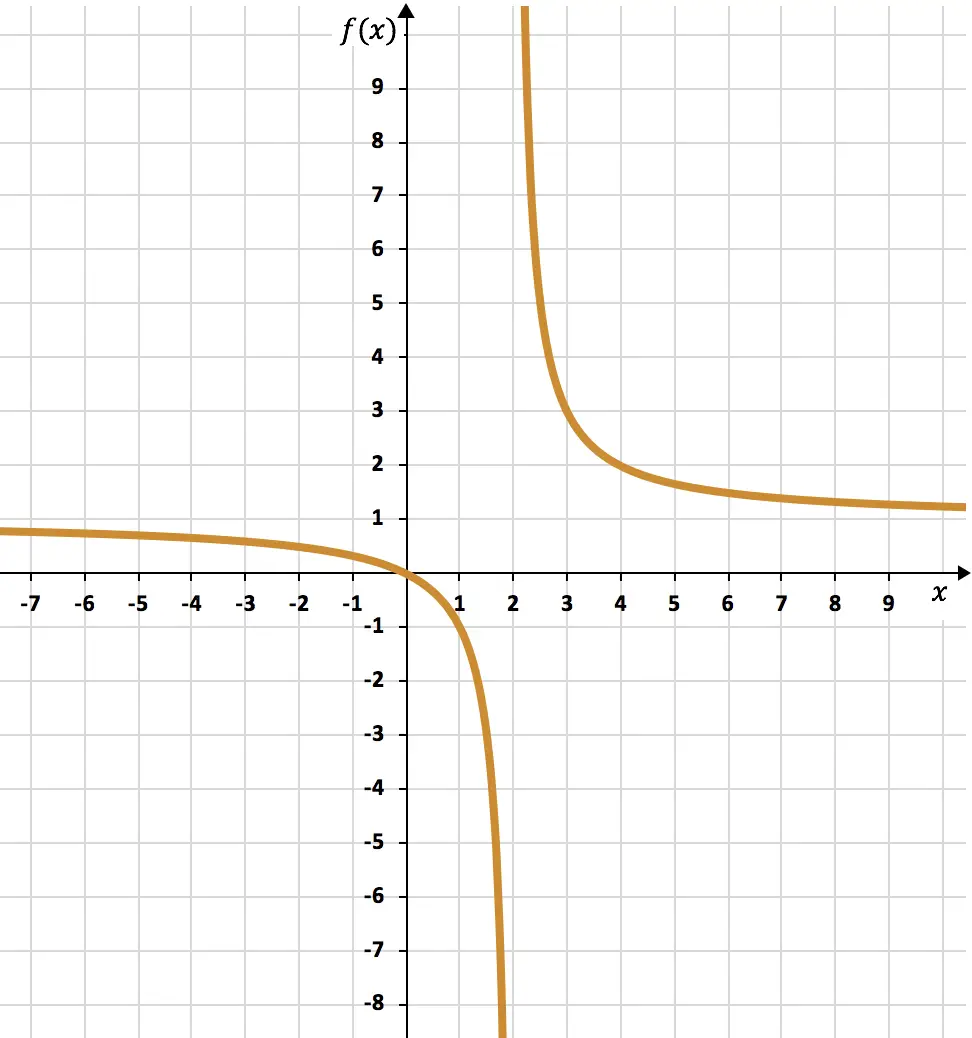
التمرين 5

ارسم بيانيًا الدالة العقلانية التالية:

أول شيء يجب فعله هو حساب مجال الدالة:

بمجرد أن نعرف مجال الدالة، نقوم بإنشاء جدول القيم:

للإنهاء، ما عليك سوى تمثيل النقاط التي تم الحصول عليها على الرسم البياني ورسم القطع الزائدة، وبالتالي تشكيل الدالة الكسرية:

تطبيقات على دالة التناسب العكسي

تظهر دالة التناسب العكسي في كثير من الحالات في الفيزياء والرياضيات.

على سبيل المثال، يتم استخدامه لوصف العلاقة بين الضغط والحجم في غاز مثالي يتعرض لدرجة حرارة ثابتة k. تسمى هذه الوظيفة قانون Boyle-Mariotte (P×V=k) وهي مثال على دالة التناسب العكسي. ومن الواضح أن مجال تعريف هذه الوظيفة يقتصر فقط على الفرع الموجب، حيث لا توجد أحجام أو ضغوط سلبية.

إن العلاقة بين شدة التيار والمقاومة الكهربائية الخاضعة لفرق محتمل ثابت تحكمها أيضًا دالة التناسب العكسي. تُعرف هذه الوظيفة بقانون أوم (V=I×R).