خطوط متحدة المستوى

في هذه الصفحة سوف تكتشف ما يعنيه عندما يكون الخطان متحدين المستوى. ستتمكن أيضًا من معرفة متى يكون الخطان متحدين المستوى، بالإضافة إلى ذلك، ستجد أمثلة وتمارين محلولة للخطوط المستوية.

ما هما الخطان المستويان؟

في الهندسة التحليلية، تعريف الخطوط المستوية هو كما يلي:

يكون الخطان متحدين المستوى عندما يكونان في نفس المستوى. لذلك، يمكن أن تكون الخطوط المستوية فقط خطوطًا قاطعة أو خطوطًا متوازية أو خطوطًا متطابقة .

علاوة على ذلك، فإن خطين متحدين المستوى يكفيان لتحديد المستوى بشكل كامل. على الرغم من أنه من الواضح أن المستوى يمكن أن يحتوي على أكثر من خطين متحدين المستوى، إلا أن كل مستوى يحتوي في الواقع على عدد لا نهائي من الخطوط.

ومن ناحية أخرى، إذا لم يكن المستقيمان متحدين المستوى، فهذا يعني أنهما متقاطعان.

أمثلة على خطوط متحدة المستوى

لكي تفهم بشكل أفضل مفهوم الخطوط المستوية، إليك مثالًا يحتوي على ثلاثة أسطر:

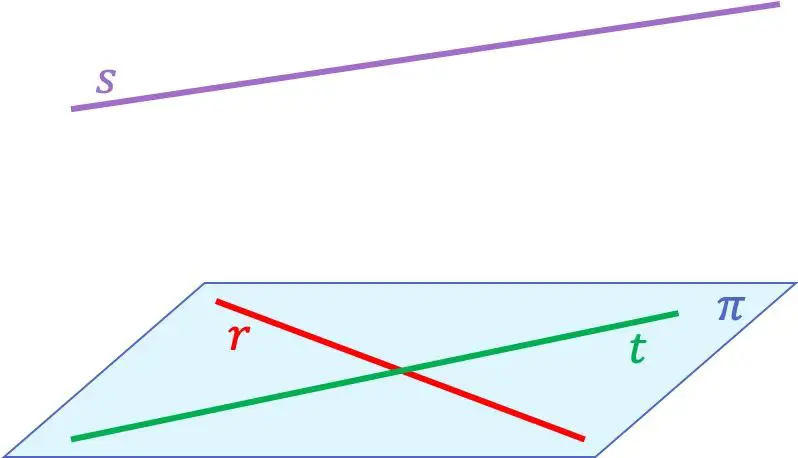
في هذه الحالة، الخطوط

و

إنهما متحدان المستوى لأنهما ينتميان إلى نفس المستوى. بدلا من ذلك، الخط المستقيم

ليس متحدا مع أي من الخطين الآخرين، لأنه متقاطع مع الخطين

و

كيف يمكنك معرفة ما إذا كان الخطان متحدان المستوى؟

كما رأينا أعلاه في شرح الخطوط المستوية، فهي لا يمكن أن تكون إلا خطوطًا قاطعة أو متوازية أو متطابقة. بمعنى آخر، الخطان المتقاطعان لن يكونا مستويين أبدًا.

ولذلك، لمعرفة ما إذا كان الخطان متحدين المستوى، يجب تحديد الموقع النسبي بينهما، وإذا كانا خطين متقاطعين أو متوازيين أو متطابقين، فهذا يعني أنهما خطان مستويان.

وبالتالي، للتحقق من المستوى المشترك لخطين، يجب عليك أولاً معرفة كيفية حساب الموضع النسبي لخطين في الفضاء . إذا كنت لا تزال غير مطلع على هذا المفهوم، فمن الأفضل أن تنظر أولاً إلى الرابط، حيث ستجد الشرح الكامل بالإضافة إلى الأمثلة والتمارين والمسائل التي تم حلها.

حل تمرين الخطوط المستوية

على سبيل المثال، سوف نقوم بحل تمرين نموذجي على الخطوط المستوية:

• حدد ما إذا كان الخطان التاليان متحدين في المستوى أم لا:

أول شيء علينا فعله هو إيجاد الموضع النسبي بين الخطين، ولهذا يجب أن نعبر عنهما باستخدام نفس نوع المعادلة. ثم سنعبر الخط المستقيم

من المعادلة العامة (أو الضمنية) إلى المعادلات البارامترية:

وبالتالي فإن متجه الاتجاه لكل سطر هو:

إن إحداثيات متجهات الاتجاه للخطين متناسبة، لذا لا يمكن أن يكونا إلا خطين متطابقين أو متوازيين. لذلك، في هذه الحالة بالذات ليست هناك حاجة لحساب الموضع النسبي الدقيق، لأن الخطوط المتوازية والخطوط المتوازية هي خطوط متحدة المستوى. لذا فإن الخطين متحدان المستوى .