▷ كيفية حل الحدود عند اللانهاية (+25 تمرينًا تم حلها)

ستجد هنا كيفية حل جميع أنواع النهايات عند اللانهاية: الدوال متعددة الحدود، والعقلانية، والأسية، مع الجذور، وعدم التحديد عند اللانهاية… بالإضافة إلى ذلك، ستتمكن من التدرب على 25 تمرينًا تم حلها خطوة بخطوة على النهايات عند x تميل إلى ما لا نهاية. .

نهاية الدالة عندما تتجه x إلى ما لا نهاية

نهاية الدالة عندما تقترب x من اللانهاية ، سواء كانت موجبة أو سالبة، يمكن أن تكون قيمة حقيقية، بالإضافة إلى ما لا نهاية، أو ناقص ما لا نهاية، أو غير موجودة. لإيجاد النهايات عند اللانهاية، عليك استبدال x بما لا نهاية.

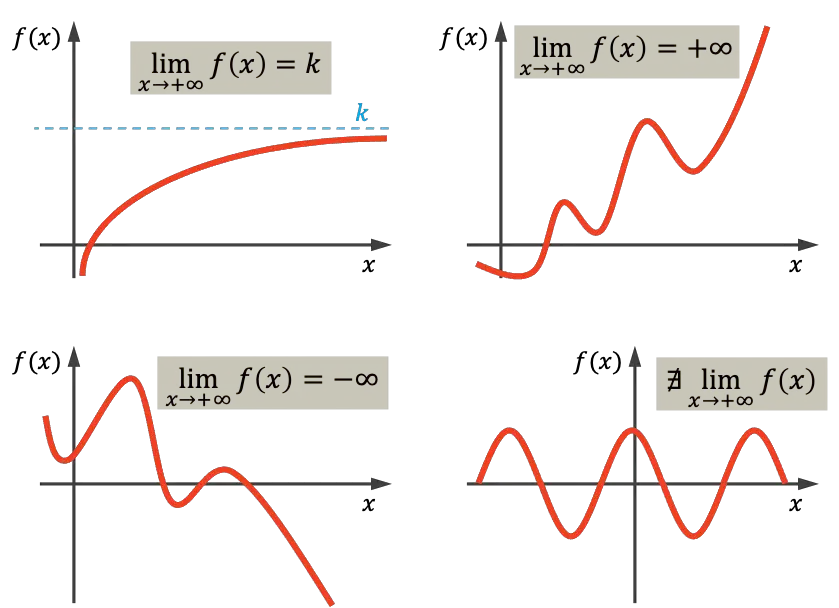
كما ترون من الرسم البياني الأول، فإن الدالة الموضحة تميل نحو القيمة الحقيقية k نحو اللانهاية، لأنها تقترب من k مع نمو x . تميل الدالة الموجودة في أعلى اليمين إلى اللانهاية عندما تقترب x من اللانهاية، لأنها تنمو إلى أجل غير مسمى مع زيادة قيمة x . من ناحية أخرى، فإن الرسم البياني الموجود في أسفل اليسار يتناقص دون توقف، وبالتالي يميل نحو سالب ما لا نهاية. وأخيرًا، الدالة الأخيرة دورية ولا تميل إلى أي قيمة، لذا لا يوجد حد لما لا نهاية في هذه الحالة.

كيفية حل الحدود في اللانهاية

لحل نهاية اللانهاية في الدوال متعددة الحدود، يجب علينا استبدال x بما لا نهاية فقط في الحد الأعلى للدالة.

على سبيل المثال، انظر إلى الحساب التالي لنهاية ما لا نهاية حيث نستبدل فقط ما لا نهاية في أحادية الحد من أعلى درجة:

$\displaystyle \lim_{x \to +\infty}(3x^2-4x+6) = 3(+\infty)^2 = \bm{+\infty}$

كما ترون في المثال، +∞ تربيع يعطي +∞، نظرًا لأن الرقم الكبير جدًا (+∞) أس 2 سيعطي دائمًا رقمًا كبيرًا جدًا (+∞).

ويحدث نفس الشيء مع الضرب: إذا قمت بضرب عدد كبير جدًا (+∞)، فستحصل دائمًا على رقم كبير جدًا (+∞). على سبيل المثال:

$3\cdot (+\infty)= +\infty.$

تحذير: لحساب حدود اللانهاية من المهم أخذ العناصر التالية بعين الاعتبار:

→ الرقم السالب المرفوع إلى الأس الزوجي يكون موجبًا. لذلك، فإن سالب ما لا نهاية مرفوعًا إلى أس زوجي يعطي زائد ما لا نهاية:

$(-\infty)^2 = +\infty$

→ الرقم السالب المرفوع إلى أس فردي يكون سالبًا. وبالتالي، فإن سالب ما لا نهاية مرفوعًا إلى أس فردي يساوي سالب ما لا نهاية:

$(-\infty)^3 = -\infty$

→ ضرب عدد سالب يغير علامة اللانهاية:

$-2(+\infty) = - \infty$

→ أي رقم مقسوما على

$\pm \infty$

يعطي 0:

$\cfrac{5}{\infty} = 0$

أمثلة على الحدود إلى ما لا نهاية

لذا يمكنك أن ترى كيف يتم حل حدود اللانهاية في كثيرات الحدود، وفيما يلي العديد من هذه الحدود التي تم حلها:

$\begin{array}{l}\displaystyle \lim_{x \to +\infty} (x^3-x^2+4)= (+\infty) ^3 = \bm{+\infty}\\[4ex]\displaystyle\lim_{x \to +\infty} (-5x+2)= -5(+\infty)= \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^2-7x+1) = (-\infty)^2 = \bm{+\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^3-x^2+4)= (-\infty) ^3 = \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to +\infty} \ \cfrac{1}{x}= \cfrac{1}{+\infty} = \bm{0}\end{array}$

حدود غير محددة إلى ما لا نهاية

لن يكون من السهل دائمًا حساب حدود اللانهاية، لأننا في بعض الأحيان سنحصل على عدم تعيين اللانهاية بين اللانهاية أو عدم تعيين اللانهاية ناقص اللانهاية.

$\cfrac{\infty}{\infty}\qquad \qquad \infty-\infty$

عندما نحصل على هذا النوع من عدم التحديد (أو الأشكال غير المحددة)، لا يمكننا معرفة النتيجة مباشرة، بل يجب علينا إجراء إجراء أولي للعثور على القيمة الحدية. وسنرى بعد ذلك كيف يتم حل النهايات غير المحددة عند اللانهاية.

اللانهائي بين اللانهائي

للعثور على نتيجة اللانهاية مقسومة على ما لا نهاية يجب علينا مقارنة درجة البسط ودرجة مقام الكسر:

إذا كانت درجة كثير الحدود البسط أقل من درجة كثير الحدود المقام، فإن عدم التعيين اللانهائي على اللانهاية يساوي الصفر.
إذا كانت درجة كثير الحدود في البسط تعادل درجة كثير الحدود المقام، فإن عدم التحديد اللانهائي على اللانهاية هو حاصل قسمة المعاملات الرئيسية لكثيرتي الحدود.
إذا كانت درجة كثير الحدود البسط أكبر من درجة كثير الحدود المقام، فإن عدم التحديد اللانهائي بين اللانهاية يعطي لانهاية أكثر أو أقل (تعتمد الإشارة على المصطلحين الرئيسيين لكثيرتي الحدود).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”></p> </p> <p style=$ على سبيل المثال، في النهاية التالية، كثير الحدود البسط هو من الدرجة الثانية، في حين أن كثير الحدود المقام هو من الدرجة الثالثة، وبالتالي فإن حل النهاية هو 0.

$\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

انظر إلى هذا المثال الآخر، الذي فيه كثيرتا حدود الدالة الكسرية من الدرجة الثانية، لذا يجب علينا قسمة معاملات حدود الدرجة الأعلى لحساب النهاية عند اللانهاية.

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

وأخيرًا، عند النهاية التالية، تكون درجة دالة البسط أكبر من درجة المقام، وبالتالي فإن عدم تحديد ما لا نهاية على ما لا نهاية يعطي ما لا نهاية. بالإضافة إلى ذلك، يتم الحصول على ما لا نهاية موجبة من البسط، ولكن ما لا نهاية سالبة من المقام، وبالتالي تكون نتيجة النهاية سالبة (الموجب بين السالب هو سالب).

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

اللانهائية اللانهائية بين اللانهاية مع الجذور

ومن ناحية أخرى، فإن درجة الدالة غير المنطقية (الدالة ذات الجذور) هي حاصل القسمة بين درجة الحد الرئيسي ومؤشر الجذر.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

لذلك، إذا كانت نهاية دالة ذات جذور تعطي عدم تحديد لا نهائي بين ما لا نهاية ، فيجب علينا تطبيق نفس القواعد الموضحة أعلاه فيما يتعلق بدرجات البسط والمقام، ولكن مع الأخذ في الاعتبار أن درجة كثيرة الحدود ذات الجذور يتم حسابها بشكل مختلف.

أنظر إلى المثال التالي للنهايات اللانهائية لدالة ذات جذور:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

درجة البسط هي 2 ودرجة المقام هي 4 (8/2=4)، وبالتالي فإن النهاية هي 0 لأن درجة البسط أقل من درجة المقام.

عدم التحديد اللانهائي بين اللانهاية مع الدوال الأسية

نمو الدالة الأسية أكبر بكثير من نمو دالة كثيرة الحدود، لذلك يجب أن نأخذ في الاعتبار أن درجة الدالة الأسية أكبر من درجة الدالة كثيرة الحدود.

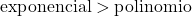$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”></p> </p> <p style=$ لذا، إذا كانت اللانهاية غير المحددة مقسومة على اللانهاية تنتج عن نهاية ذات دوال أسية، فيجب علينا ببساطة تطبيق نفس القواعد التي تشرح درجات البسط والمقام، ولكن مع الأخذ في الاعتبار أن الدالة الأسية ذات ترتيب أعلى من كثيرة الحدود.

بالإضافة إلى ذلك، إذا كانت لدينا دوال أسية في بسط ومقام القسمة، فإن الدالة الأسية ذات القاعدة الأكبر ستكون هي ذات الترتيب الأعلى.

$\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

في هذا المثال، يتكون المقام من دالة أسية، لذا فهو ذو مرتبة أعلى من البسط. ولذلك، فإن صيغة اللانهاية غير المحددة بين اللانهاية تعطي 0.

اللانهائي ناقص اللاحتمية اللانهائية

يعتمد حل المعادلة اللانهائية ناقص عدم التحديد اللانهائي على ما إذا كانت الدالة تحتوي على كسور أم جذور. لذلك دعونا نرى كيفية حل هذا النوع من عدم التحديد لهاتين الحالتين المختلفتين.

عدم التحديد لانهائي ناقص لانهائي مع الكسور

عندما يحدث عدم التحديد اللانهائي ناقص اللانهائي في جمع أو طرح الكسور الجبرية ، يجب علينا أولاً إجراء جمع أو طرح الكسور ثم حساب النهاية.

دعونا نرى كيفية حساب اللانهاية اللانهاية ناقص اللانهاية في دالة تحتوي على كسور عن طريق حل مثال خطوة بخطوة:

$\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)$

نحاول أولاً حساب الحد:

$\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}$

لكننا حصلنا على عدم التعيين ∞-∞.

يجب علينا أولا طرح الكسور. للقيام بذلك، نقوم بتقليل الكسور إلى مقام مشترك، أي أننا نضرب بسط ومقام كسر واحد في مقام الآخر:

$\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}$

والآن بعد أن أصبح للكسرين نفس المقام، يمكننا دمجهما في كسر واحد:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}$

نحن نتعامل مع البسط والمقام:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}$

وأخيرًا نحسب الحد مرة أخرى:

$\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}$

في هذه الحالة فإن عدم التحديد اللانهائي بين اللانهاية يعطي +∞ لأن درجة البسط أكبر من درجة المقام.

عدم التعيين لانهائي ناقص لانهائي مع الجذور

عندما يحدث عدم التحديد اللانهائي ناقص اللانهائي في الجمع الجذري أو الطرح ، يجب علينا أولاً ضرب الدالة وتقسيمها بالتعبير الجذري المترافق ثم إيجاد النهاية.

دعونا نرى كيفية حل اللانهاية اللانهائية ناقص اللانهاية في دالة غير عقلانية باتباع مثال خطوة بخطوة:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)$

نحاول أولاً حل نهاية الدالة باستخدام الجذور:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}$

ومع ذلك، حصلنا على الصيغة غير المحددة ∞-∞. لذا، لكي تعرف مقدار عدم التحديد الذي يساوي اللانهاية ناقص اللانهاية، عليك تطبيق الإجراء الموضح.

بما أن الدالة لها جذور، فإننا نضرب الدالة بأكملها ونقسمها بالتعبير غير العقلاني المقترن:

$\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}$

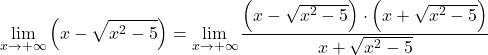
يتوافق التعبير الجبري للبسط مع الهوية البارزة لمنتج المجموع والفرق، لذلك يمكننا تبسيط التعبير:

$\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}$

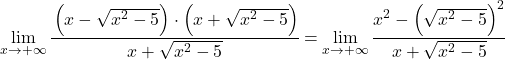
والآن نقوم بتبسيط جذر النهاية، حيث إنها مربعة:

$\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}$

نحن نتعامل مع بسط الكسر:

$\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}$

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}$

وأخيرًا، نعيد حساب الحد:

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}$

وبالتالي فإن نتيجة النهاية هي 0، لأن أي عدد مقسوم على ما لا نهاية يساوي صفرًا.

حل تمارين على النهايات عند اللانهاية

التمرين 1

أوجد الحدود التالية لدالة الرسم البياني:

$\displaystyle\lim_{x\to -\infty}f(x)$

$\displaystyle\lim_{x\to +\infty}f(x)$

$\displaystyle\lim_{x\to -1^-}f(x)$

$\displaystyle\lim_{x\to -1^+}f(x)$

$\displaystyle\lim_{x\to 1^-}f(x)$

$\displaystyle\lim_{x\to 1^+}f(x)$

انظر الحل

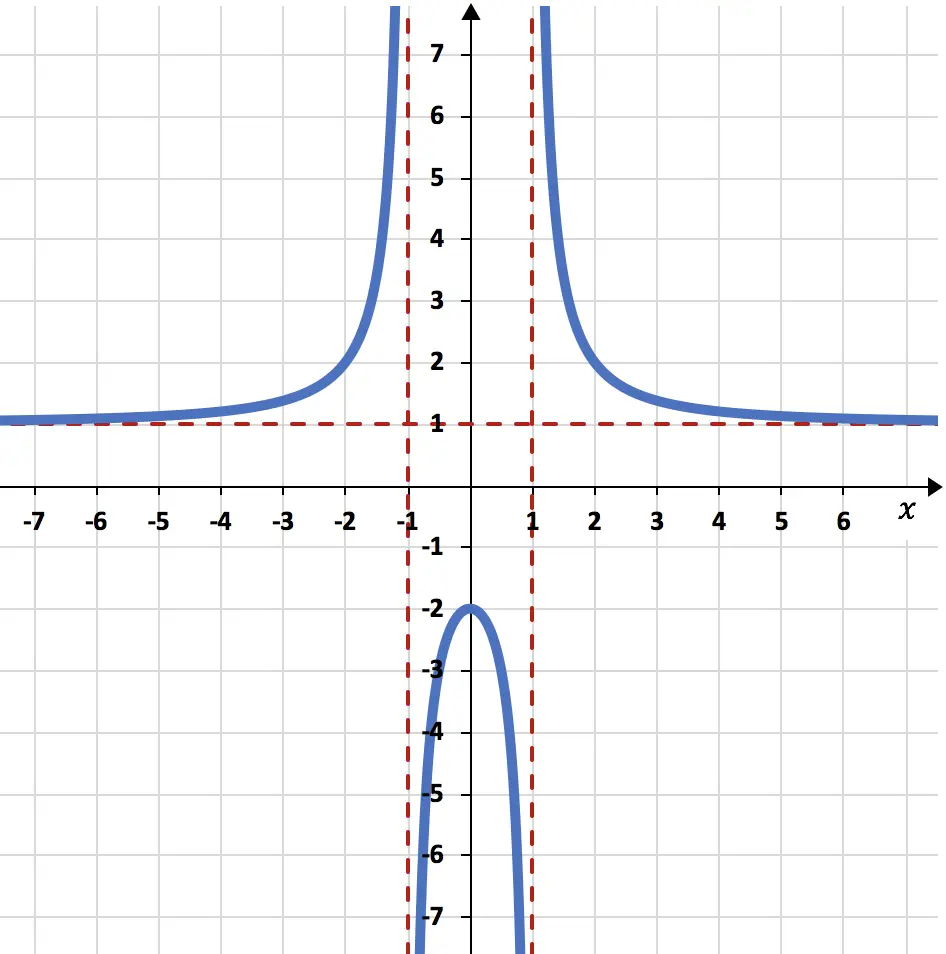
نهاية الدالة عندما تتجه x نحو سالب ما لا نهاية وزائد ما لا نهاية يعطي 1:

$\displaystyle\lim_{x\to -\infty}f(x)=1$

$\displaystyle\lim_{x\to +\infty}f(x)=1$

الحدود الجانبية للدالة على اليسار واليمين عند النقطة x=-1 هي على التوالي زائد ما لا نهاية وناقص ما لا نهاية:

$\displaystyle\lim_{x\to -1^-}f(x)=+\infty$

$\displaystyle\lim_{x\to -1^+}f(x)=-\infty$

وأخيرًا، فإن الحدود الجانبية للدالة عندما تميل x إلى 1 تساوي ناقص ما لا نهاية وزائد ما لا نهاية:

$\displaystyle\lim_{x\to 1^-}f(x)=-\infty$

$\displaystyle\lim_{x\to 1^+}f(x)=+\infty$

تمرين 2

حل النهاية مع اقتراب x بالإضافة إلى ما لا نهاية للدالة التالية:

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1)$

انظر الحل

لإيجاد النهاية عند اللانهاية، نحتاج إلى استبدال x بما لا نهاية في الحد الأعلى من كثير الحدود:

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1) = (+\infty)^2= \bm{+\infty}$

التمرين 3

احسب الحد إلى ما لا نهاية للدالة متعددة الحدود التالية:

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5)$

انظر الحل

لإيجاد النهاية عند اللانهاية، نستبدل x بما لا نهاية في أعلى درجة لكثيرة الحدود ونجري الحسابات:

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5) = -3(+\infty)^2= -3\cdot (+\infty) = \bm{-\infty}$

التمرين 4

حل الحد اللانهائي على الأقل للدالة كثيرة الحدود التالية:

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4)$

انظر الحل

لحساب النهاية عند اللانهاية، نستبدل x بـ ناقص اللانهاية في الدرجة الأعلى من كثير الحدود ونقيم الدالة:

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4) = 6(-\infty)^2= 6\cdot (+\infty) = \bm{+\infty}$

بما أن سالب ما لا نهاية هو مربع، فإن إشارة ما لا نهاية تصبح موجبة.

التمرين 5

أوجد النهاية عند اللانهاية للدالة المنطقية التالية:

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5}$

انظر الحل

لتحديد نهاية ما لا نهاية، نستبدل x بـ زائد ما لا نهاية عند الحد الأعلى لبسط ومقام الكسر:

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5} = \cfrac{7}{2\cdot(+\infty)}=\frac{7}{+\infty}=\bm{0}$

تذكر أن أي رقم مقسوم على زائد أو ناقص ما لا نهاية يساوي 0.

التمرين 6

حل النهاية التالية عند اللانهاية:

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x)$

انظر الحل

لحساب النهاية عندما تتجه x نحو ±∞ للدالة، انظر ببساطة إلى أحادية الحد لأعلى درجة للدالة:

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x) = -(-\infty)^3= -(-\infty)= \bm{+\infty}$

التمرين 7

احسب نهاية الدالة التالية عندما تقترب x من اللانهاية السالبة:

$\displaystyle \lim_{x \to -\infty} (-4x^2+4)$

انظر الحل

في هذه الحالة، يكفي استبدال ما لا نهاية للحد التربيعي:

$\displaystyle \lim_{x \to -\infty} (-4x^2+4) = -4(-\infty)^2= -4\cdot (+\infty) = \bm{-\infty}$

التمرين 8

أوجد نهاية الدالة الأسية التالية عندما تقترب x من اللانهاية:

$\displaystyle \lim_{x \to +\infty} 2^x$

انظر الحل

على الرغم من أنها دالة أسية، إلا أن عملية حل النهاية هي نفسها: استبدل x بما لا نهاية.

$\displaystyle \lim_{x \to +\infty} 2^x = 2^{+\infty}=\bm{+\infty}$

التمرين 9

حل النهاية اللانهائية للدالة الأسية التالية:

$\displaystyle \lim_{x \to +\infty} 5^{-x}$

انظر الحل

لحل هذا الحد يجب عليك استخدام خصائص الكسور:

$\displaystyle \lim_{x \to +\infty} 5^{-x} = 5^{-(+\infty)}=5^{-\infty}= \cfrac{1}{5^{+\infty}}= \cfrac{1}{\infty} =\bm{0}$

التمرين 10

حل النهاية التالية عند اللانهاية:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

انظر الحل

النهاية تعطي عدم التعيين ناقص اللانهاية بين زائد اللانهاية. درجة البسط أكبر من درجة المقام، وبالتالي فإن النهاية غير المحددة تساوي زائد ما لا نهاية. ومع ذلك، بما أن القسمة هي سالب ما لا نهاية على ما لا نهاية موجب، فإن النتيجة هي ما لا نهاية سالبة.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

التمرين 11

أصلح الحد غير المحدد التالي:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

انظر الحل

في هذه المشكلة، يتم الحصول على الصيغة غير المعينة ما لا نهاية على ما لا نهاية من حاصل قسمة كثيرتي الحدود من نفس الدرجة، وبالتالي فإن نتيجة النهاية غير المعينة هي تقسيم معاملاتهما الرئيسية:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

التمرين 12

احسب النهاية التالية على الأقل إلى ما لا نهاية:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

انظر الحل

درجة التعبير الجبري للبسط أقل من درجة التعبير للمقام، وبالتالي فإن عدم التعيين +∞/+∞ يعطي 0:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

التمرين 13

حل النهاية غير المحددة التالية للدالة ذات الجذور:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

انظر الحل

تعبير البسط يقع تحت جذري، وبالتالي فإن درجته هي 7/3. ومن ناحية أخرى، فإن مقام كثير الحدود هو تربيعي. وبما أن 7/3>2، فإن النهاية تعطي المزيد من اللانهاية:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=\bm{+\infty}$

التمرين 14

حدد النهاية اللانهائية للدالة التالية بالكسور:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

انظر الحل

في هذا التمرين نحصل على عدم التحديد ناقص ما لا نهاية مقسومًا على ناقص ما لا نهاية مع درجة البسط أكبر من درجة المقام، وبالتالي:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

التمرين 15

أوجد النهاية اللانهائية على الأقل للدالة التالية:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

انظر الحل

كثير الحدود المقام هو تربيعي، في حين أن كثير الحدود البسط خطي. لذلك، فإن عدم التحديد اللانهائي مقسومًا على اللانهاية يعطي 0.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

التمرين 16

حل الحد اللانهائي على الأقل للدالة التالية:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

انظر الحل

البسط أكبر من المقام بدرجة واحدة، وبالتالي فإن نتيجة الصورة غير المحددة ∞/∞ ستكون لا نهائية. بالإضافة إلى ذلك، علامة اللانهاية ستكون سالبة لأن الموجب بين السالب يترجم إلى سالب:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

التمرين 17

حل النهاية التالية عند اللانهاية:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

انظر الحل

الدالة الأسية ذات ترتيب أعلى من الدالة كثيرة الحدود، وبالتالي فإن النهاية ستعطي ما لا نهاية. لكن بقسمة الموجب على السالب تكون علامة اللانهاية سالبة:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

التمرين 18

احسب النهاية اللانهائية للدالة التالية ذات الجذر التربيعي:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}$

انظر الحل

يتكون البسط من جذر تربيعي، وبالتالي فإن درجته هي 2/2=1. ومن ثم تكون درجة البسط مساوية لدرجة المقام، وبالتالي يتم حل اللانهائية بين اللانهاية على النحو التالي:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}= \cfrac{\sqrt{4(+\infty)^2}}{-2(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt{4}}{-2}=\cfrac{2}{-2}=\bm{-1}$

التمرين 19

حل النهاية اللانهائية للدالة التالية بجذرين:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

انظر الحل

درجة البسط هي 7/3=2.33 ودرجة المقام هي 5/2=2.5. ولذلك، بما أن درجة البسط أقل من درجة المقام، فإن الحد اللانهائي غير المحدد بين ما لا نهاية هو 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

التمرين 20

احسب الحد التالي:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

انظر الحل

بغض النظر عن درجة البسط، نظرًا لأن لدينا دالة أسية في المقام، فإن نتيجة الصيغة غير المحددة اللانهائية على اللانهاية هي 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

التمرين 21

حدد النهاية اللانهائية للدالة المنطقية التالية:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)$

انظر الحل

أولاً، نحاول حساب النهاية عن طريق التعويض بما لا نهاية في الدالة:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}$

لكننا نجد عدم التعيين ∞ – ∞. ولذلك، فإننا نختصر الكسور إلى قاسم مشترك:

$\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}$

وبما أن الكسرين لهما الآن نفس المقام، فيمكننا دمجهما في كسر واحد:

$\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}$

نقوم بعمل قوسين للبسط:

$\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}$

وأخيرًا نحدد الحد:

$\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}$

في هذه الحالة عدم التحديد ∞/∞ يعطي +∞ لأن درجة البسط أكبر من درجة المقام.

التمرين 22

حل نهاية الدالة الكسرية التالية عندما تقترب x من 0:

$\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)$

انظر الحل

نحاول أولاً حساب الحد كالمعتاد:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}$

لكننا حصلنا على الصيغة غير المحددة ∞-∞. لذلك يجب علينا تقليل كسور الدالة إلى قاسم مشترك.

في هذه الحالة، x ⁴ هو مضاعف لـ x ² ، لذلك ببساطة عن طريق ضرب بسط ومقام الكسر الثاني في x ² سنضمن أن كلا الكسرين لهما نفس المقام:

$\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}$

يمكننا الآن طرح الكسرين:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}$

نحاول حل الحد مرة أخرى:

$\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}$

لكننا في النهاية نصل إلى عدم تعيين ثابت يبدأ من الصفر. لذلك من الضروري حساب الحدود الجانبية للدالة.

$\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

$\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

في الختام، بما أن النهايتين الجانبيتين للدالة عند النقطة x=0 تعطيان -∞، فإن حل النهاية هو -∞:

$\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}$

التمرين 23

حل النهاية اللانهائية للدالة التالية مع الجذور:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)$

انظر الحل

في محاولة لحل النهاية، نحصل على اللانهاية اللانهاية ناقص اللانهاية:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}$

لذلك، بما أن الدالة تحتوي على جذور، فيجب ضربها وتقسيمها بالتعبير الجذري المترافق:

$\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}$

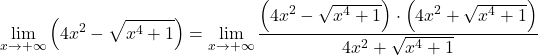
في البسط لدينا الناتج الملحوظ للمجموع والفرق، وهو ما يساوي الفرق بين المربعين. حتى الآن:

$\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}$

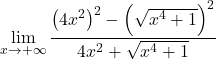
نحن نبسط الجذر إلى المربع:

$\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}$

نحن نعمل على البسط:

$\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}$

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}$

وأخيرا نجد الحد:

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}$

في هذه الحالة، تكون اللانهاية اللانهائية مقسومة على اللانهاية أكثر لا نهائية لأن درجة البسط أكبر من درجة المقام (تذكر أن الجذر التربيعي يقلل الدرجة بمقدار اثنين:

$\sqrt{x^4} = x^{4/2} = x^2$

التمرين 24

حل النهاية عندما تقترب x من اللانهاية للدالة غير المنطقية التالية:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)$

انظر الحل

أولاً، نحاول حساب الحد كالمعتاد:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}$

ولكن هذا يؤدي إلى عدم تحديد الفرق في اللانهاية. لذلك، بما أن الدالة لها جذور، فيجب علينا ضرب التعبير وتقسيمه على الجذر المترافق:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}$

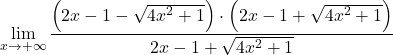
نقوم بتجميع المساواة الملحوظة لبسط الكسر:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}$

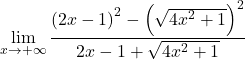
نحل الجذر التربيعي:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

نحن نحل الهوية البارزة لمربع الفرق:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

نحن نعمل على البسط:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}$

$\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}$

وأخيرًا، نحسب قيمة النهاية عند اللانهاية:

$\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =$

على الرغم من وجود مربع x في المقام، إلا أن درجته هي في الواقع 1 لأنه موجود داخل الجذر:

$\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .$

ولذلك فإن نتيجة عدم التعيين -∞/+∞ هي تقسيم معاملات x من أعلى درجة، لأن درجة البسط هي نفس درجة المقام.

$\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}$

لاحظ أنه نظرًا لوجود حدين من الدرجة الأولى في المقام

$\bigl(2x$

$\sqrt{4x^2}\bigr)$

، لحل عدم التحديد -∞/+∞ من الضروري أخذ جميع معاملات حدود الدرجة الأولى، أي

$2$

$2x$

و ال

$\sqrt{4}$

$\sqrt{4x^2}.$

التمرين 25

احسب النهاية عندما تقترب x من 1 للدالة التالية بالكسور:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)$

انظر الحل

من خلال محاولة جعل النهاية نحصل على النهاية غير المحددة لما لا نهاية ناقص ما لا نهاية:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}$

ولذلك يجب علينا اختزال الكسور إلى مقام مشترك، أو بمعنى آخر، يجب علينا ضرب بسط ومقام أحد الكسرين في مقام الآخر:

$\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}$

وبما أن الكسرين لهما نفس المقام، فيمكننا تجميعهما معًا:

$\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}$

نحن نعمل:

$\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}$

$\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}$

ونحاول حل النهاية مرة أخرى:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}$

لكننا نجد عدم التعيين صفرًا مقسومًا على صفر. لذلك يجب علينا تحليل كثيرات الحدود في البسط والمقام:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}$

نقوم الآن بتبسيط الكسر بإزالة العامل المتكرر في البسط والمقام:

$\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}$

وأخيرًا، نحل الحد:

$\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}$

نهاية الدالة عندما تتجه x إلى ما لا نهاية

كيفية حل الحدود في اللانهاية

أمثلة على الحدود إلى ما لا نهاية

حدود غير محددة إلى ما لا نهاية

اللانهائي بين اللانهائي

اللانهائية اللانهائية بين اللانهاية مع الجذور

عدم التحديد اللانهائي بين اللانهاية مع الدوال الأسية

اللانهائي ناقص اللاحتمية اللانهائية

عدم التحديد لانهائي ناقص لانهائي مع الكسور

عدم التعيين لانهائي ناقص لانهائي مع الجذور

حل تمارين على النهايات عند اللانهاية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

التمرين 7

التمرين 8

التمرين 9

التمرين 10

التمرين 11

التمرين 12

التمرين 13

التمرين 14

التمرين 15

التمرين 16

التمرين 17

التمرين 18

التمرين 19

التمرين 20

التمرين 21

التمرين 22

التمرين 23

التمرين 24

التمرين 25

اترك تعليقاً إلغاء الرد