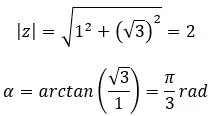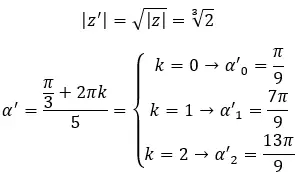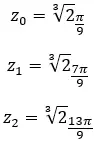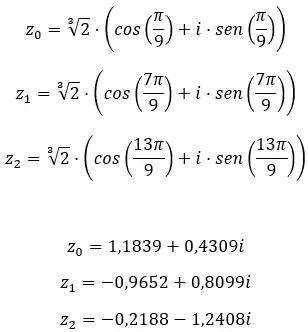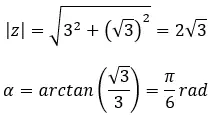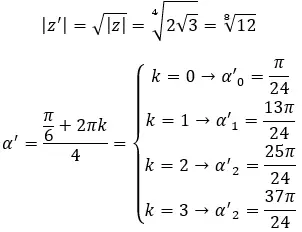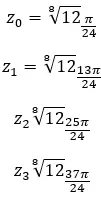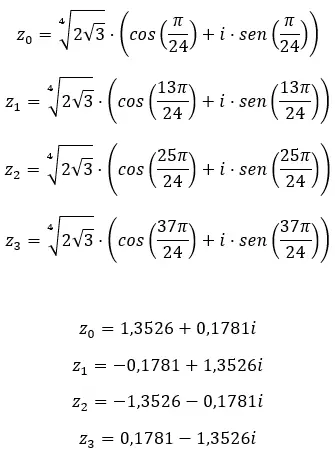حساب جذور الأعداد المركبة أمر بسيط للغاية. حسنًا، بمجرد أن تفهم الإجراء، يصبح متكررًا تمامًا. وبعد ذلك سنشرحها ونعطيك مثالاً لتتعلم كيفية تطبيقها في تمارين حقيقية.
الجذور النونية للأعداد المركبة
مفهوم الجذر النوني يعادل قول جذر الرتبة n، لذلك يتم استخدام نفس الطريقة لحساب الجذر التربيعي والجذر الخامس لعدد مركب. وبطبيعة الحال، فإن عدد الحلول سوف يتغير تبعا لهذا الترتيب.
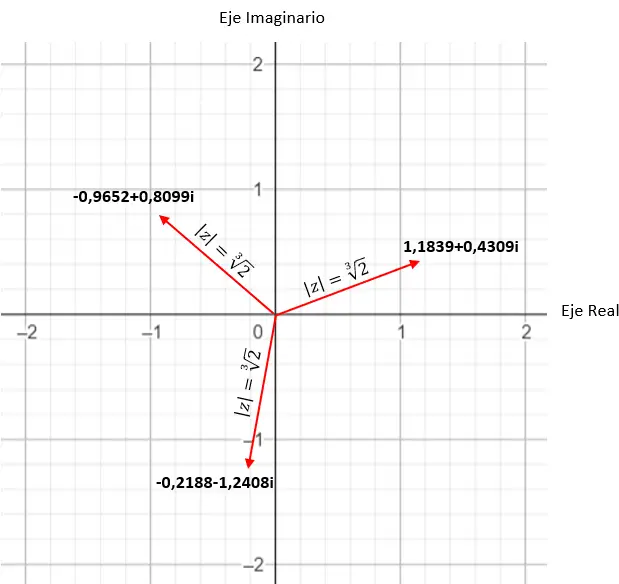
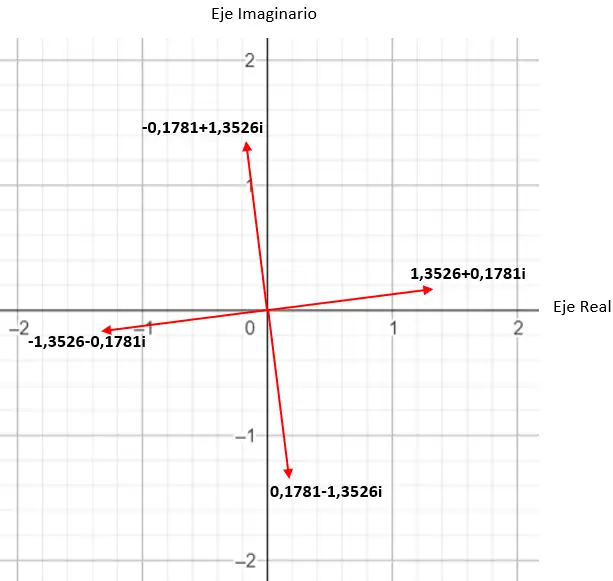
على سبيل المثال، إذا قمنا بحساب الجذر الرابع لمعقد، فسنحصل على 4 حلول مختلفة. وإذا عبرنا عنه بالمستوى المركب نرى أنه يتشكل مضلع منتظم له أربعة أضلاع، يتمركز حول أصل المستوى. هذه خاصية مثيرة جدًا للاهتمام، والتي سنراها بالتفصيل لاحقًا (في قسم الأمثلة).
الآن بعد أن أوضحنا هذا المفهوم، سنرى كيفية حساب جذر عدد مركب في الصورة القطبية (استخدام هذا الترميز هو الأكثر راحة لحل الجذر.). ببساطة، تحتاج إلى حساب جذر المعامل والتعبير عن الوسيطة بدلالة n. بمعنى آخر، جذر العدد المركب التالي (z):
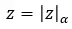
هذه المبالغ لحساب:
- الوحدة النمطية: الجذر n للوحدة الأولية.
- الوسيطة: أضف 2πk بالراديان أو 360k بالدرجات إلى الوسيطة، واقسمها على n.
رياضياً، لحساب الوحدة والوسيطة نستخدم الصيغتين التاليتين:
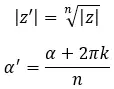
حيث ك = 0، 1، 2، …، ن-1.
ولذلك فإننا نعبر عن النتيجة على النحو التالي:
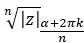
للتوضيح، الحلول n التي سنحصل عليها من خلال حل هذا الجذر سيتم تشكيلها بواسطة نفس الوحدة وn من الوسائط المختلفة.
أمثلة لحساب الجذور النونية للمجمعات
سنرى الآن بعض الأمثلة على حساب الجذور النونية للأعداد المركبة. نوصي بمحاولة حلها بنفسك، وعندما تنتهي، راجع الإصلاح. ولا تنس أن الطريقة موضحة أعلاه.
أوجد الجذر الثالث للعدد المركب: 1 + i √3 .
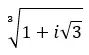
أوجد الجذر الرابع للعدد المركب: 3+i √ 3 .
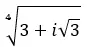
التعرف على جذور الأعداد المركبة
- ارقام مركبة
- العمليات على الأعداد المركبة
- القوى المعقدة
- خصائص الأعداد المركبة