في هذه الصفحة نشرح ما هو ثلاثي الحدود المربع الكامل وكيف يتم حسابه. بالإضافة إلى ذلك، ستتمكن من رؤية العديد من الأمثلة والتدرب على تمارين ثلاثية الحدود المربعة المثالية خطوة بخطوة.
ما هو ثلاثي الحدود المربع الكامل؟
من الواضح، قبل رؤية معنى ثلاثية الحدود المربعة الكاملة، عليك أن تعرف ما هي ثلاثيات الحدود ، لذلك أوصي بإلقاء نظرة على هذه الصفحة المرتبطة (حيث يتم شرحها بالتفصيل) قبل المتابعة.
لذا فإن تعريف ثلاثية الحدود المربعة الكاملة هو كما يلي:
في الرياضيات، ثلاثية الحدود المربعة الكاملة ، والمعروفة أيضًا باسم TCP ، هي ثلاثية الحدود التي يتم الحصول عليها عن طريق تربيع ذات الحدين.
لذلك، فإن ثلاثية الحدود المربعة الكاملة تتكون من كثيرة الحدود بمربعين كاملين وحد آخر هو حاصل الضرب المزدوج لأساسي هذين المربعين.

كما ترون من الصيغتين أعلاه، يتم الحصول على ثلاثية الحدود المربعة الكاملة من هويتين بارزتين (أو منتجات بارزة)، وهذا هو سبب أهميتها. على وجه التحديد، يتم العثور على ثلاثية حدود مربعة مثالية عند حل مربع الجمع أو مربع الطرح .
أمثلة ثلاثية الحدود مثالية
للانتهاء من فهم مفهوم ثلاثية حدود المربع الكامل، سنشرح مثالين خطوة بخطوة:
مثال 1
![]()
هذا المثال عبارة عن ثلاثية حدود مربعة كاملة لأنه في تعبيرها الجبري يوجد مربعان كاملان (أي أن لهما جذرًا تربيعيًا دقيقًا)، حيث
![]()
و9 يعادل
![]()
و3 مرفوعة على التوالي للقوة اثنين:
![]()
![]()
وأكثر من ذلك، الحد الأخير المتبقي من ثلاثية الحدود
![]()
ويتم الحصول عليها بضرب أساسات المربعين السابقين معًا وفي 2:
![]()
لذا فإن كل الهوية البارزة الكاملة في هذا التمرين ستكون:
![]()
مثال 2
![]()
هذا المثال الآخر هو أيضًا ثلاثية حدود مربع كامل لأنه تم استيفاء الشروط الثلاثة الضرورية: حدان يتوافقان مع مربعين كاملين، وحد آخر هو نتيجة ضرب أساسات هذه المربعات مع بعضها البعض وفي 2.
![]()
![]()
![]()
في هذه الحالة، ثلاثي الحدود المربع الكامل له أحادي حد سلبي، وبالتالي فهو يتوافق مع تطور المساواة الملحوظة للفرق التربيعي:
![]()
كيفية تحليل ثلاثية الحدود المربعة المثالية
في الجبر، هناك مشكلة شائعة جدًا وهي تحليل مربع ثلاثي الحدود الكامل (PCT). في حال كنت لا تعرف ما يعنيه ذلك، فإن تحليل كثيرة الحدود يعني تحويل تعبيرها إلى حاصل ضرب العوامل.
وبالتالي، من أجل تحليل هذا النوع من ثلاثية الحدود الجبرية، يجب احترام القواعد التالية:
- يجب أن يحتوي ثلاثي الحدود على مربعين كاملين، وهو ما سنسميه
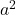
و
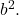
- يجب أن يكون الحد الثالث المتبقي من ثلاثي الحدود مساويًا للمنتج المزدوج لقاعدتي المربعين الكاملين، وهو ما يتوافق رياضيًا مع التعبير
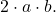
- سيكون ثلاثي الحدود المُعامل
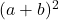
إذا كانت جميع حدود ثلاثية الحدود للمربع الكامل موجبة، وإلا، إذا كان المنتج المزدوج لأساسات المربعات له إشارة سالبة، فإن ثلاثية الحدود المحللة ستكون
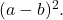
لإكمال فهم الإجراء، سنقوم بحل تمرين خطوة بخطوة:
- عامل المعادلة الثلاثية المربعة الكاملة التالية:
![]()
أول شيء علينا القيام به هو تحديد ما إذا كانت ثلاثية الحدود تحتوي على عنصرين يمثلان مربعين كاملين، أو بعبارة أخرى، إذا كان جذرها التربيعي لا يعطي عددًا عشريًا. في هذه المشكلة
![]()
هو مربع المتغير
![]()
و36 هو مربع 6:
![]()
![]()
وبالتالي فإن ثلاثي الحدود يحتوي على مربعين كاملين.
ثانيًا، يجب التأكد مما إذا كان الحد الوسيط يعادل حاصل الضرب المزدوج للجذرين المحسوبين في الخطوة السابقة:
![]()
يتم احترام هذه القاعدة أيضًا.
ثم يتم استيفاء جميع الشروط. لذلك، فإن ثلاثية الحدود المربعة الكاملة المحللة هي ذات الحدين المكونة من الجذرين الموجودين (
![]()
والرقم 6) تربيع:
![]()
وبما أن الحد الأوسط سالب، فيجب علينا أيضًا وضع علامة الطرح بين قوسين. من ناحية أخرى، إذا كان إيجابيا علينا أن نضيف مبلغا:
![]()
من الناحية المنطقية، يعد التحليل إجراءً معقدًا، لذا، بالإضافة إلى محاولة القيام بالتمرين أدناه، أوصي بالنظر إلى هذه الأمثلة لتحليل كثيرات الحدود . في هذا الرابط، نشرح أيضًا طريقة تُستخدم ليس فقط لتحليل ثلاثيات الحدود، ولكن أيضًا أي نوع من كثيرات الحدود، وبنفس السرعة.
حل تمارين على ثلاثية الحدود المربعة الكاملة
قم بتحويل ثلاثيات الحدود التالية إلى ثنائيات مربعة من خلال تطبيق الصيغة المقابلة:
![]()
![]()
![]()
![]()
![]()
لتحويل ثلاثية حدود مربعة مثالية إلى قوة ذات حدين مربعين، يجب عليك استخدام الصيغ الخاصة بالمتطابقات البارزة لمربع المجموع ومربع الفرق، وهي:
![]()
![]()
حتى الآن:
![]()
![]()
![]()
![]()
![]()
⬇⬇⬇ لا تنسوا أنه بإمكانكم كتابة جميع أسئلتكم أدناه في التعليقات! ⬇⬇⬇