تماثل الدالة: الدالة المتماثلة وغير المتماثلة

نشرح في هذه المقالة ما هي الدوال المتماثلة (الدوال الزوجية والفردية) وكيفية دراسة تماثل الدالة. ستتمكن أيضًا من رؤية خصائص هذه الأنواع من الوظائف، وأخيرًا، ستتمكن من التدرب على التمارين التي تم حلها خطوة بخطوة للوظائف المتماثلة.

ما هي وظيفة متماثلة؟

الدالة المتماثلة هي دالة يمكن من خلالها العثور على محور التماثل في تمثيله الرسومي. هناك نوعان من الدوال المتماثلة: الدوال الزوجية، المتناظرة حول المحور Y، والدوال الفردية، المتناظرة حول أصل الإحداثيات.

تذكر أن محور التماثل هو خط وهمي يقسم أي شيء إلى جزأين بحيث تكون نقطتيهما المتقابلتين على مسافة متساوية من بعضهما البعض.

حتى الوظائف

الدوال الزوجية هي دوال متناظرة حول المحور y، أي أن المحور Y هو محور تناظر الدالة.

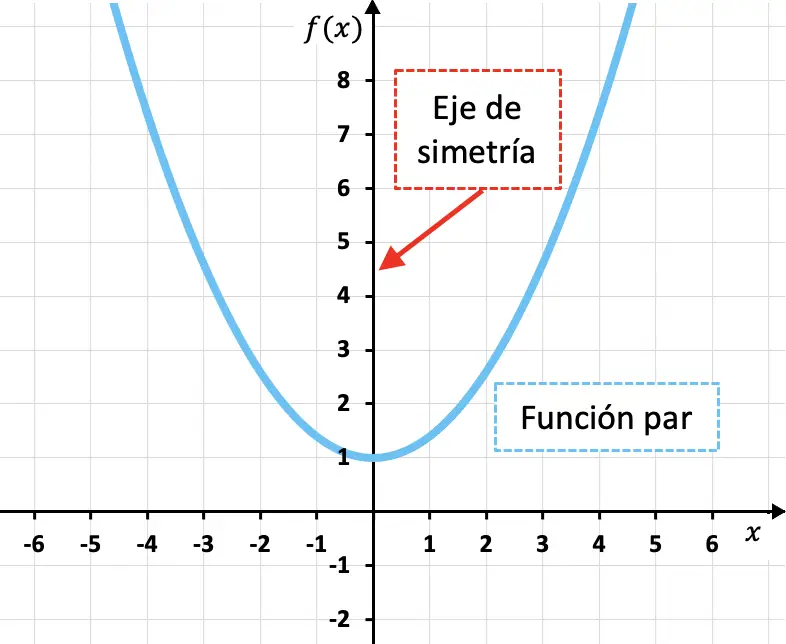
حتى وظيفة متماثلة

كما ترى في الدالة التربيعية الموضحة أعلاه، فإن صورة الدالة الزوجية لأي قيمة للمتغير المستقل (x) تعادل صورة الدالة للقيمة المقابلة (-x). بمعنى آخر، من الناحية الرياضية، تكون الدالة زوجية إذا استوفت الشرط التالي:

f(x)=f(-x)

الدوال الزوجية هي نوع من الدوال المتماثلة، والآن دعونا نرى كيف تبدو الدوال الفردية.

وظائف غريبة

الدوال الفردية هي دوال متناظرة بالنسبة لأصل الإحداثيات، أي بالنسبة للنقطة (0،0).

أدناه يمكنك رؤية دالة فردية مرسومة بيانيا:

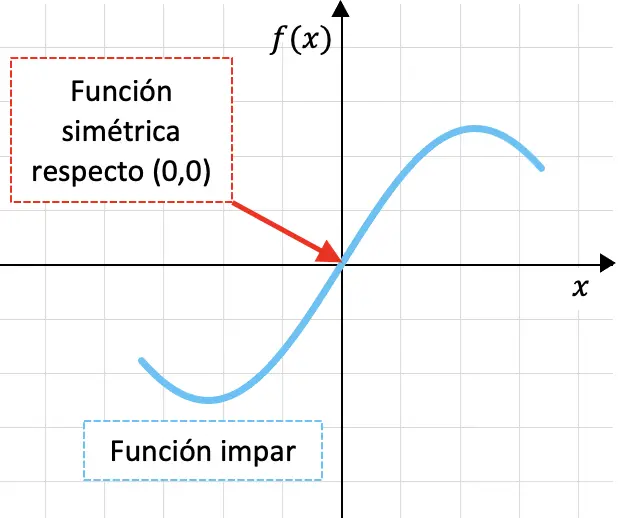
وظيفة متماثلة غريبة

حقيقة أن الدالة متماثلة حول أصل الإحداثيات تعني أنه إذا قمنا بطي الرسم البياني للدالة أولاً عبر محور OY ثم عبر محور OX، فإن الرسم البياني للدالة سوف يتداخل.

جبريًا، تكون الدالة فردية إذا تحققت العلاقة التالية بين صورها:

f(-x)=-f(x)

إن معرفة تماثل الدالة مفيد جدًا لتمثيلها، لأنه بمعرفة نصف الرسم البياني فقط يمكننا رسم الجزء الآخر بسرعة.

كيفية العثور على التماثل للدالة

لدراسة تماثل دالة، يجب علينا حساب صورة

-x

أي أنه من الضروري الحساب

f(-x).

لذا، اعتمادًا على نتيجة الصورة، سيكون تماثل الدالة كما يلي:

  1. إذا تم ملؤه

    f(-x)=f(x)

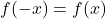
    ، تكون الدالة زوجية وبالتالي متناظرة بالنسبة للمحور Y.

  2. إذا تم ملؤه

    f(-x)=-f(x)

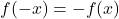
    ، فإن الدالة فردية وبالتالي فهي متناظرة بالنسبة لأصل الإحداثيات.

  3. إذا لم يتم استيفاء أي من الشروط المذكورة أعلاه، فهي دالة غير متماثلة (ليس لها محور تماثل).

على سبيل المثال، دعونا نحلل تماثل الدالة التكعيبية التالية:

f(x)=x^3

لدراسة تماثل الدالة نقوم بالحساب

f(-x):

f(-x)=(-x)^3=-x^3

التعبير الجبري الناتج يعادل تعبير الدالة الأصلي ولكنه تغير في الإشارة، أو بمعنى آخر، تم تحقيق المساواة التالية:

f(-x)=-f(x)

وبالتالي فإن الدالة فردية وبالتالي متناظرة بالنسبة لأصل الإحداثيات (0,0).

خصائص الوظائف المتماثلة

تتميز الوظائف المتماثلة بالخصائص التالية:

  • مجموع دالتين زوجيتين/فرديتين يساوي دالة زوجية/فردية أخرى.
  • حاصل ضرب دالتين زوجيتين أو دالتين فرديتين يعطي دالة زوجية.
  • مشتقة الدالة الزوجية/الفردية هي دالة زوجية/فردية.
  • التركيب بين دالتين زوجيتين/فرديتين يعادل دالة زوجية/فردية.
  • الدالة الوحيدة الزوجية والفردية، أي المتناظرة بالنسبة إلى محور OY وفيما يتعلق بنقطة الأصل، هي الدالة

    f(x)=0.

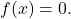
حل مسائل تماثل الدالة

التمرين 1

أوجد تماثل الدالة التالية:

f(x)=x^4+5x^2

لحساب تماثل الدالة، علينا إيجاد القيمة

f(-x):

f(-x)=(-x)^4+5(-x)^2=x^4+5x^2

أي قوة لعدد سالب مرفوع إلى الأس تعطي رقمًا موجبًا، لذلك في هذه الحالة تكون المعادلة التالية صحيحة:

f(-x)=f(x)

وبالتالي فإن الدالة زوجية وبالتالي فهي متناظرة حول المحور y (المحور Y).

تمرين 2

ادرس تماثل الدالة العقلانية التالية:

f(x)=\cfrac{7x^2}{3+x^3}

لتحديد تماثل الدالة، نقوم بذلك

f(-x):

f(-x)=\cfrac{7(-x)^2}{3+(-x)^3}=\cfrac{7x^2}{3-x^3}

في هذه المشكلة، لم يتم استيفاء شرط التماثل، لأن صورة

-x

لا يساوي

f(x)

ولا ل

-f(x).

f(-x)\neq f(x)\neq -f(x)

وبالتالي فإن الدالة ليس لها محور تماثل، بل هي بالأحرى دالة غير متماثلة.

التمرين 3

احسب تماثل الدالة التالية:

f(x)=2x|x|

لتحليل تماثل الدالة، علينا الحساب

f(-x):

\begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}

وفي هذه الحالة يكون التعبير الناتج مثل التعبير الأصلي ولكن مع تغيير الإشارة، فتتحقق المعادلة التالية:

f(-x)=-f(x)

وبالتالي فإن الدالة فردية وبالتالي متناظرة بالنسبة لأصل الإحداثيات (0,0).

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top