في هذه المقالة سوف نرى كيفية تمثيل أي نوع من الوظائف على الرسم البياني. بالإضافة إلى ذلك، ستجد تمارين محلولة خطوة بخطوة حول تمثيل الوظائف على الرسم البياني.
كيفية تمثيل دالة على الرسم البياني
لتمثيل دالة على الرسم البياني، يجب تنفيذ الخطوات التالية:
- أوجد مجال الدالة.
- احسب نقاط القطع للدالة باستخدام المحاور الديكارتية.
- احسب الخطوط المقاربة للدالة.
- دراسة رتابة الوظيفة وإيجاد الحدود القصوى لها.
- دراسة انحناء الدالة وإيجاد نقاط انعطافها .
- ارسم النقاط المقطوعة، والخطوط المقاربة، والنقاط القصوى النسبية، ونقاط الانعطاف، ثم ارسم الدالة.
مثال لتمثيل دالة
لكي تتمكن من رؤية كيفية تمثيل الدالة بيانيًا، سنحل التمرين التالي خطوة بخطوة:
- ارسم الدالة المنطقية التالية على الرسم البياني:
![]()
أول شيء يجب فعله هو حساب مجال الدالة . هذه دالة كسرية، لذا نحتاج إلى جعل المقام مساويًا للصفر لمعرفة الأرقام التي لا تنتمي إلى مجال الدالة:
![]()
![]()
لذلك، عندما تكون x 1، سيكون المقام 0 وبالتالي لن تكون الدالة موجودة. وبالتالي فإن مجال الدالة يتكون من جميع الأعداد الحقيقية باستثناء x=1.
![]()
للعثور على نقطة التقاطع مع المحور X يجب علينا حل المعادلة
![]()
نظرًا لأن الدالة دائمًا لها قيمة 0 على المحور X:
![]()
![]()
على المدى
![]()
يتضمن ذلك تقسيم الجانب الأيسر بأكمله، حتى نتمكن من ضربه في الجانب الأيمن بأكمله:
![]()
![]()
![]()
وبالتالي فإن نقطة التقاطع مع محور OX هي:
![]()
ولإيجاد نقطة التقاطع مع المحور Y نقوم بالحساب
![]()
لأن x دائمًا 0 على المحور Y:
![]()
وبالتالي فإن نقطة القطع مع محور OY هي:
![]()
في هذه الحالة، عندما تمر الدالة عبر أصل الإحداثيات، فإن نقطة التقاطع مع المحور X تتزامن مع نقطة التقاطع مع المحور Y.
بمجرد أن نعرف المجال ونقاط القطع، نحتاج إلى حساب الخطوط المقاربة للدالة .
لمعرفة ما إذا كانت الدالة لها خطوط مقاربة رأسية، نحتاج إلى حساب نهاية الدالة عند نقاط لا تنتمي إلى المجال (في هذه الحالة x=1). وإذا كانت النتيجة لا نهائية، فهو خط مقارب عمودي. حتى الآن:
![]()
بما أن نهاية الدالة عندما تميل x إلى 1 تعطي ما لا نهاية، فإن x=1 هو خط مقارب رأسي:
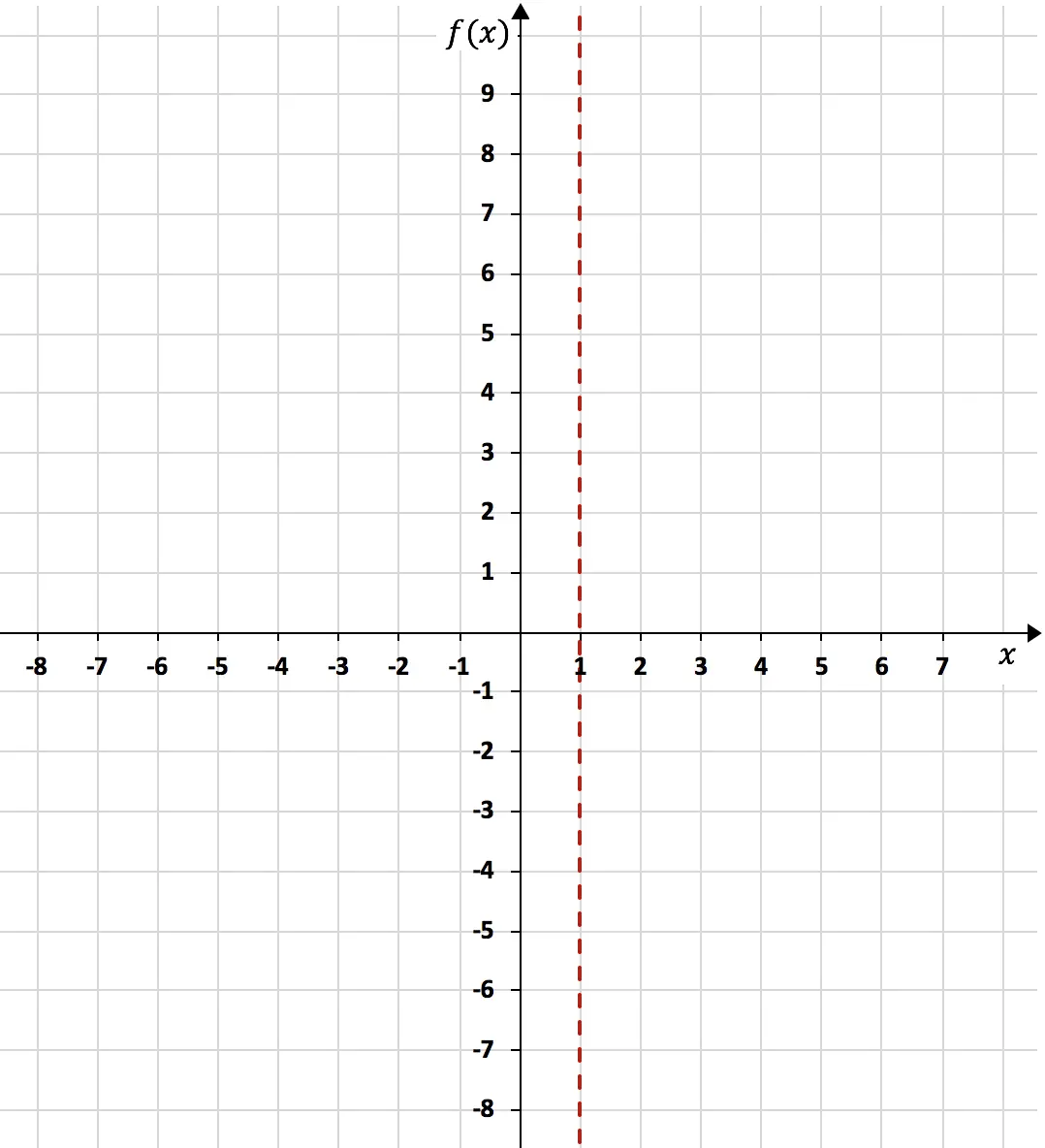
بمجرد حساب الخط المقارب الرأسي، من الضروري حساب الحدود الجانبية للدالة بالنسبة إليه. بما أننا لا نعرف إذا كانت الدالة ستميل إلى -∞ أو +∞ عندما تقترب من x=1 من اليسار، ولا نعرف متى تقترب من x=1 من اليمين.
وبالتالي، ننتقل إلى حساب الحد الجانبي الأيسر للدالة عند x=1:
![]()
لحساب الحدود الجانبية عند نقطة ما عدديًا، يجب علينا استبدال رقم في الدالة القريبة جدًا من النقطة. في هذه الحالة، نريد رقمًا قريبًا جدًا من 1 على اليسار، مثل 0.9. لذلك نعوض بالنقطة 0.9 في الدالة:
![]()
الحدود الجانبية للخط المقارب يمكن أن تعطي فقط +∞ أو -∞. وبما أنه من خلال استبدال رقم قريب جدًا من 1 على اليسار في الدالة، حصلنا على نتيجة سلبية، فإن النهاية على اليسار هي -∞:
![]()
الآن نقوم بنفس الإجراء مع حدود الجانب الأيمن:
![]()
نستبدل رقمًا قريبًا جدًا من 1 على اليمين في الدالة. على سبيل المثال النقطة 1.1:
![]()
في هذه الحالة، تكون نتيجة الحد الجانبي رقمًا موجبًا. وبالتالي فإن النهاية على اليمين هي +∞:
![]()
في الختام، عند x=1، تميل الدالة نحو سالب اللانهاية على اليسار، وزائد اللانهاية على اليمين:
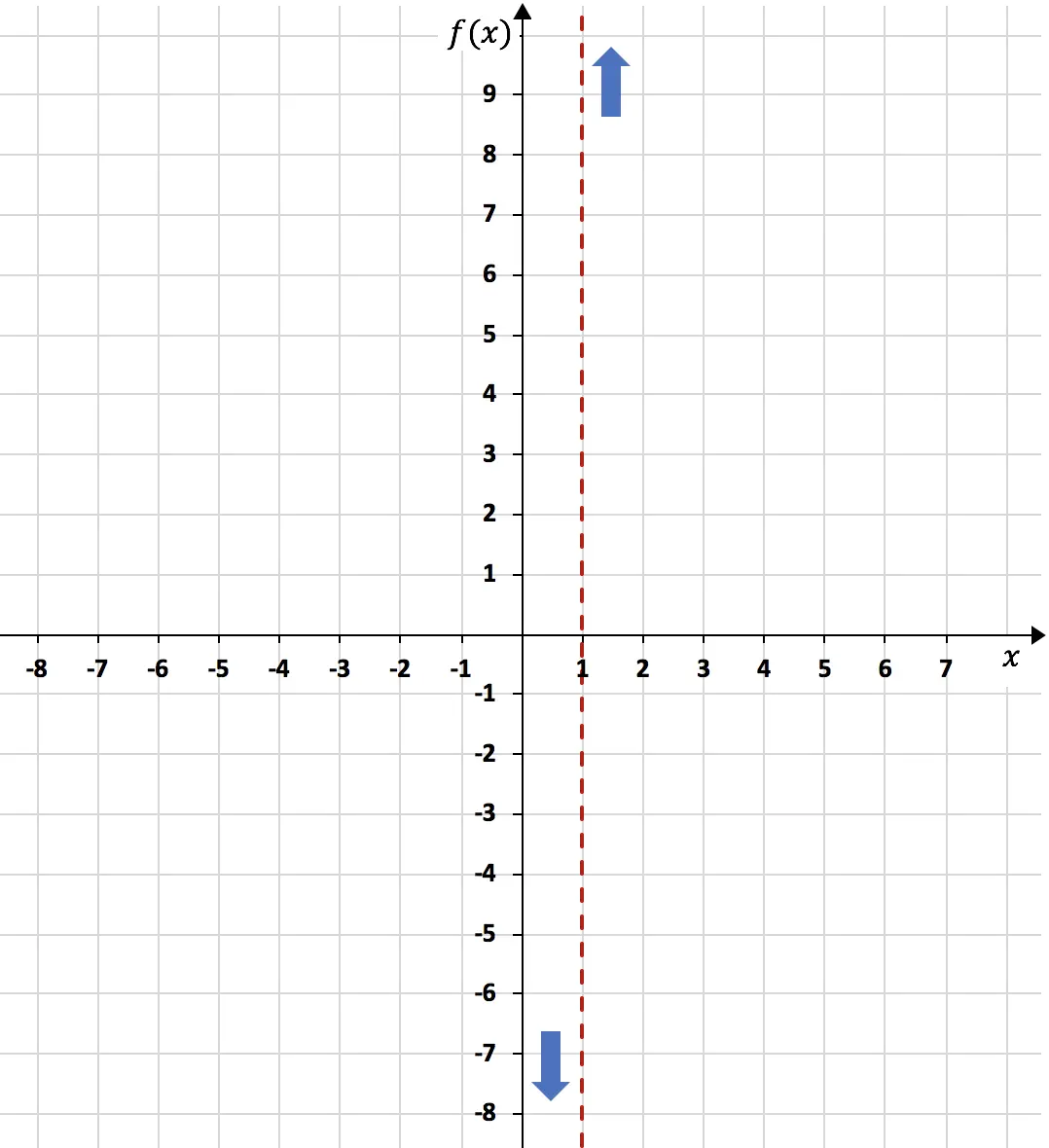
ومن ناحية أخرى، فإن الخط المقارب الأفقي للدالة سيكون نتيجة النهاية اللانهائية للدالة. حتى الآن:
![]()
تذكر كيفية حساب الحدود اللانهائية للوظائف العقلانية:
![\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”></p>
</p>
</div>
<p style=](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c969e4b99985b44006e57d554ff0247_l3.png) النهاية اللانهائية للدالة أعطتنا +∞، لذا فإن الدالة ليس لها خط تقارب أفقي.
النهاية اللانهائية للدالة أعطتنا +∞، لذا فإن الدالة ليس لها خط تقارب أفقي.
نحن الآن نحسب الخط المقارب المائل. الخطوط المقاربة المائلة هي من النموذج
![]()
. و
![]()
ويتم حسابها بالصيغة التالية:
![]()
![]()
يبدو x كما لو أن مقامه هو 1:
![]()
إنها تقسيم الكسور، لذلك نضربها عرضيًا:
![]()
![]()
ونحسب الحد:
![]()
إذن م = 1. الآن نحسب
![]()
مع الصيغة التالية:
![]()
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty](https://mathority.org/wp-content/ql-cache/quicklatex.com-10dfa8fdcfbf0c978e02374654a66b7d_l3.png)
لكننا حصلنا على ما لا نهاية من عدم التعيين ناقص ما لا نهاية، لذلك يتعين علينا اختزال الحدين إلى مقام مشترك. للقيام بذلك، نضرب الحد x ونقسمه على مقام الكسر:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-70026c2aed1bb58a120f8c18423d9ef5_l3.png)
الآن بعد أن أصبح لكلا المصطلحين نفس المقام، يمكننا تجميعهما:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-7702287a02af6d8e3dddaa3f0c6eb1b5_l3.png)
وأخيرا نحل الحد:
![Rendered by QuickLaTeX.com \displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-feb5faa9dc5d3b68d3273ad4d75d2bb1_l3.png)
إذن n = 1. وبالتالي فإن الخط المقارب المائل هو:
![]()
![]()
![]()
بمجرد قيامنا بحساب الخط المقارب المائل، فإننا نمثله على نفس الرسم البياني من خلال إنشاء جدول القيم:
![]()

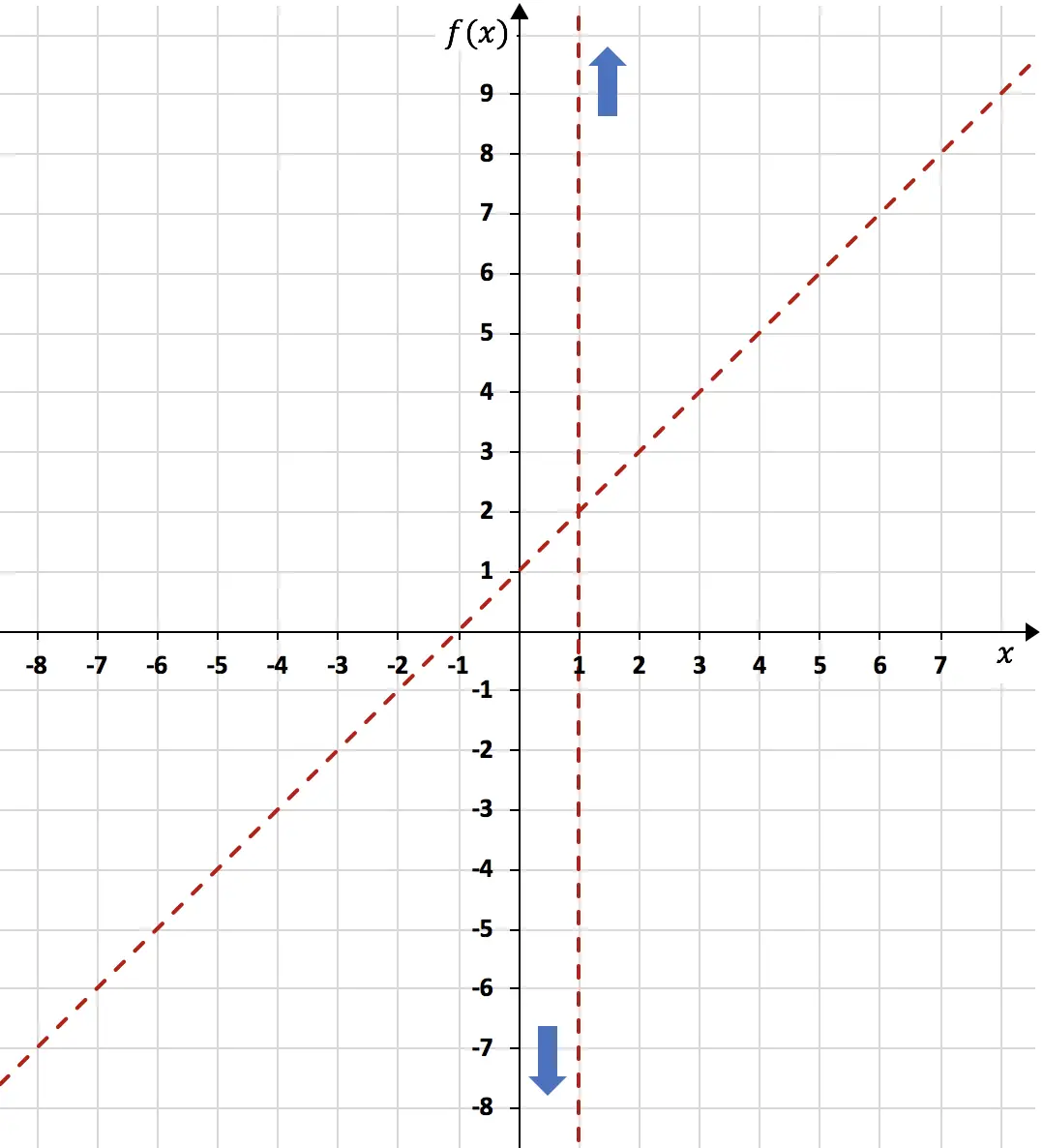
الآن بعد أن عرفنا جميع الخطوط المقاربة للدالة، نحتاج إلى تحليل رتابة الوظيفة . وهذا يعني أننا بحاجة إلى دراسة الفترات التي تزيد فيها الدالة والفترات التي تقل فيها. لذلك نحسب المشتقة الأولى للدالة:
![]()
![]()
والآن نجعل المشتقة تساوي 0 ونحل المعادلة:
![]()
![]()
على المدى
![]()
يتضمن ذلك تقسيم الجانب الأيسر بأكمله، حتى نتمكن من ضربه في الجانب الأيمن بأكمله:
![]()
![]()
نستخرج العامل المشترك لحل المعادلة التربيعية:
![]()
لكي يكون الضرب يساوي 0، يجب أن يكون أحد عنصري الضرب صفراً. لذلك، نجعل كل عامل يساوي 0 ونحصل على كلا حلي المعادلة:
![Rendered by QuickLaTeX.com \displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55127e675ce8f7742db17d565c2ae507_l3.png)
نمثل الآن على خط الأعداد جميع النقاط الحرجة التي تم العثور عليها، أي النقاط التي لا تنتمي إلى المجال (x=1) وتلك التي تلغي المشتقة (x=0 وx=2):

ونحسب إشارة المشتقة في كل فترة لنعرف ما إذا كانت الدالة تزيد أم تنقص. لذلك نأخذ نقطة في كل فترة (وليس النقاط الحرجة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند تلك النقطة:
![]()
![]()
![]()
![]()
![]()
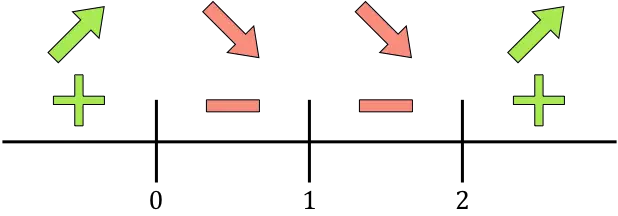
إذا كانت المشتقة موجبة فهذا يعني أن الدالة تتزايد، وإذا كانت المشتقة سالبة فهذا يعني أن الدالة تتناقص. وبالتالي فإن فترات النمو والانخفاض هي:
نمو:
![]()
ينقص:
![]()
علاوة على ذلك، عند x=0، تنتقل الدالة من الزيادة إلى التناقص، لذا فإن x=0 هو الحد الأقصى النسبي للدالة. وعند x=2، تنتقل الدالة من التناقص إلى الزيادة، لذا فإن x=2 هو الحد الأدنى النسبي للدالة.
أخيرًا، نعوض الحدود القصوى الموجودة في الدالة الأصلية لإيجاد الإحداثي Y للنقاط:
![]()
![]()
وبالتالي فإن الحدود النسبية للوظيفة هي:
الحد الأقصى على النقطة
![]()
الحد الأدنى للنقطة
![]()
نحن نمثل الحد الأقصى والحد الأدنى على الرسم البياني:
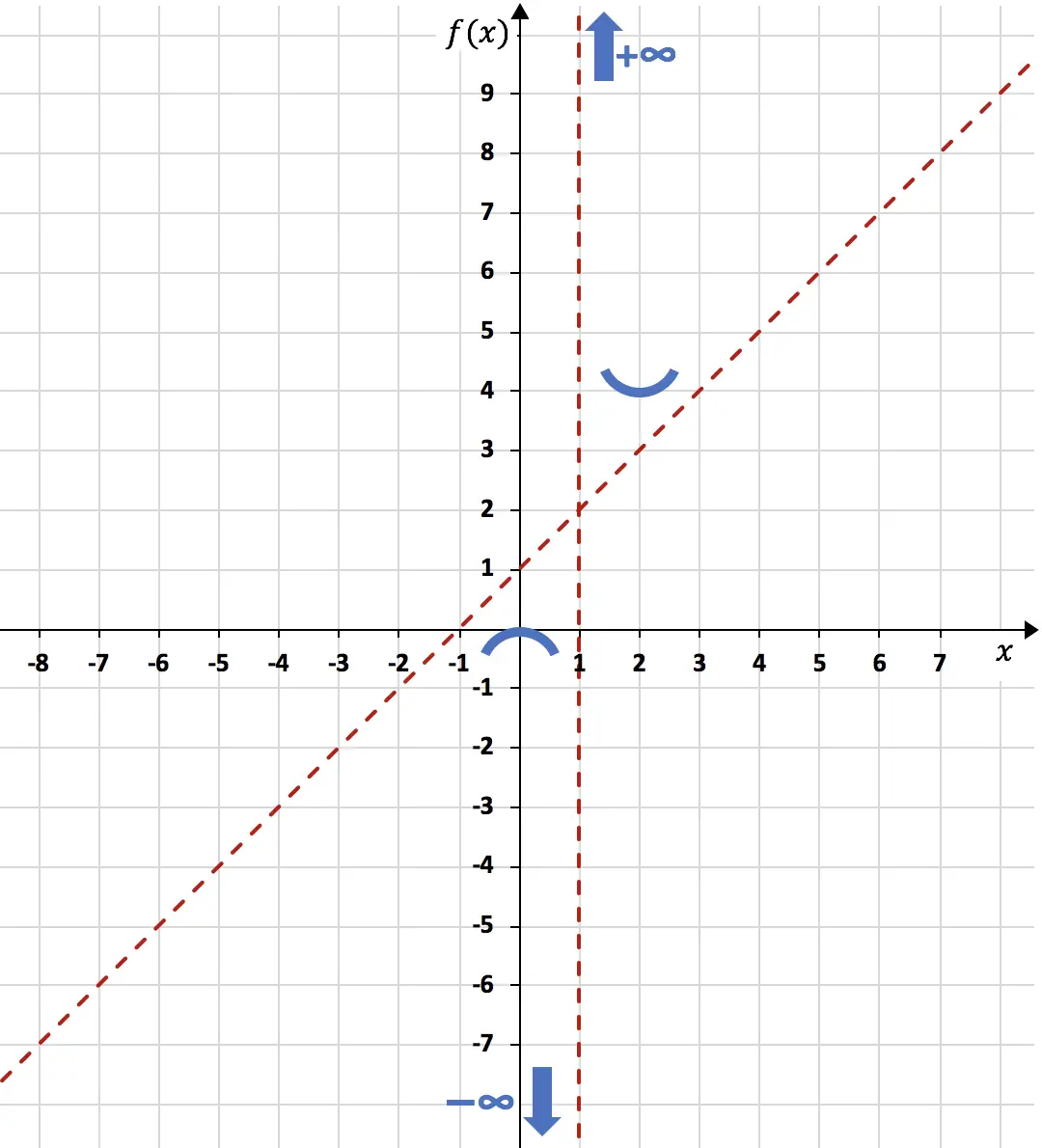
وأخيرا، يكفي دراسة انحناء الدالة ، أي دراسة فترات تقعر وتحدب الدالة. للقيام بذلك، نحسب مشتقتها الثانية:
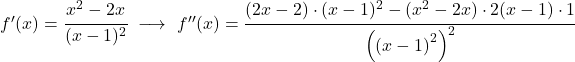
![]()
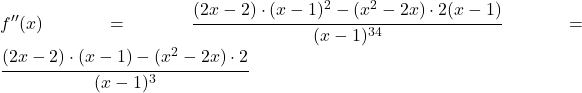
![]()
![]()
والآن نساوي المشتقة الثانية بالصفر ونحل المعادلة:
![]()
![]()
![]()
![]()
2 لن يساوي 0 أبدًا، وبالتالي فإن المعادلة
![]()
لا يوجد حل.
نحن نمثل الآن على خط الأعداد جميع النقاط الحرجة التي تم العثور عليها، أي النقاط التي لا تنتمي إلى المجال (x=1) وتلك التي تلغي المشتقة الثانية (في هذه الحالة لا يوجد شيء لم يحدث):

ونحسب إشارة المشتقة في كل فترة لنعرف ما إذا كانت الدالة محدبة أم مقعرة. لذلك نأخذ نقطة في كل فترة (وليس النقاط المفردة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند هذه النقطة:
![]()
![]()
![]()

وأخيرًا نستنتج فترات تقعر وتحدب الدالة. إذا كانت المشتقة الثانية موجبة، فهذا يعني أن الدالة محدبة.
![]()
وإذا كانت المشتقة الثانية سالبة فهذا يعني أن الدالة مقعرة
![]()
. وبالتالي فإن فترات التقعر والتحدب هي:
محدب
![]()
:
![]()
مقعر
![]()
:
![]()
ومع ذلك، على الرغم من وجود تغيير في الانحناء عند x=1، إلا أنها ليست نقطة انعطاف. لأن x=1 لا ينتمي إلى مجال الدالة.
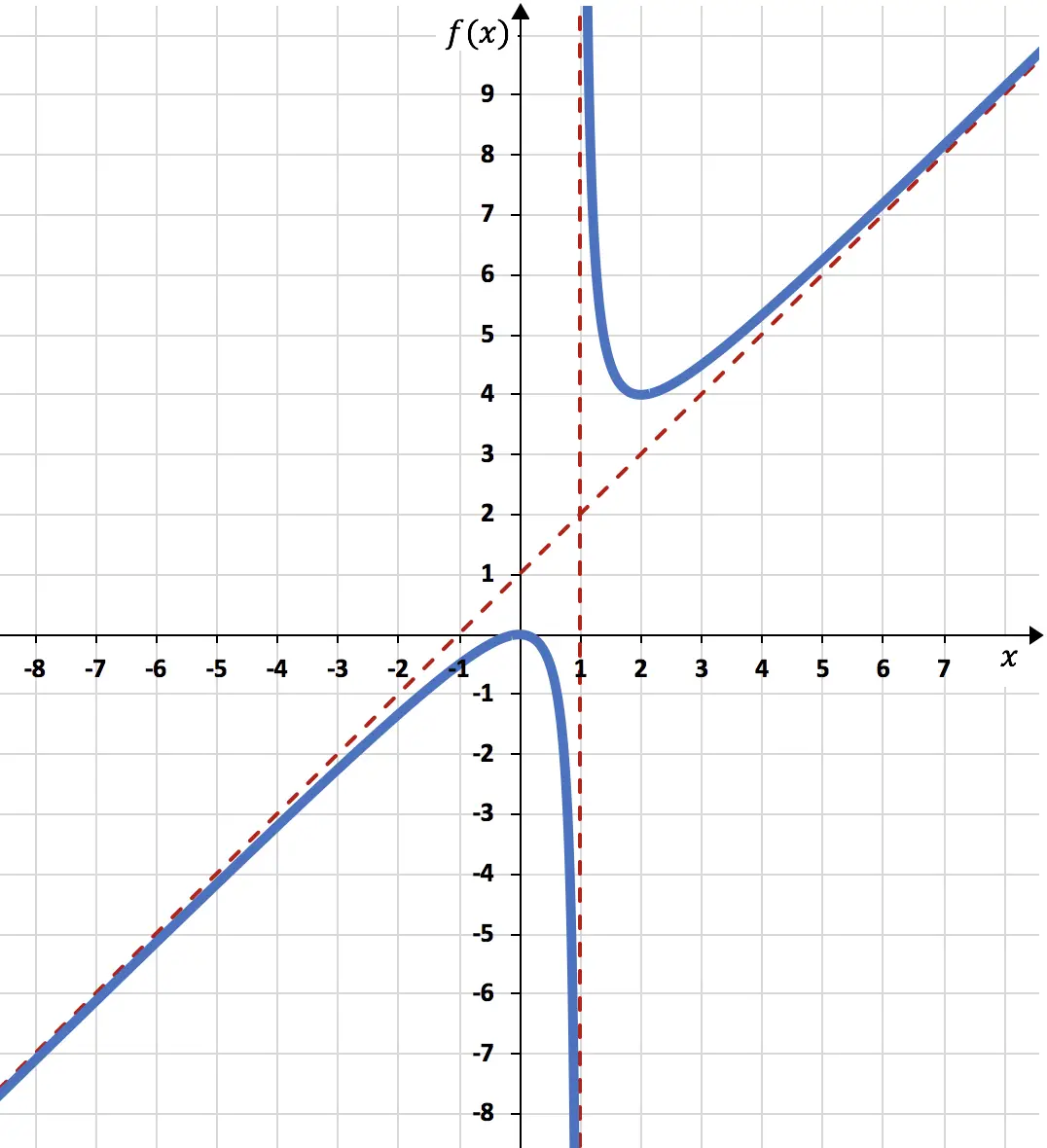
حتى نتمكن من الانتهاء من تمثيل الوظيفة باستخدام كل ما حسبناه:
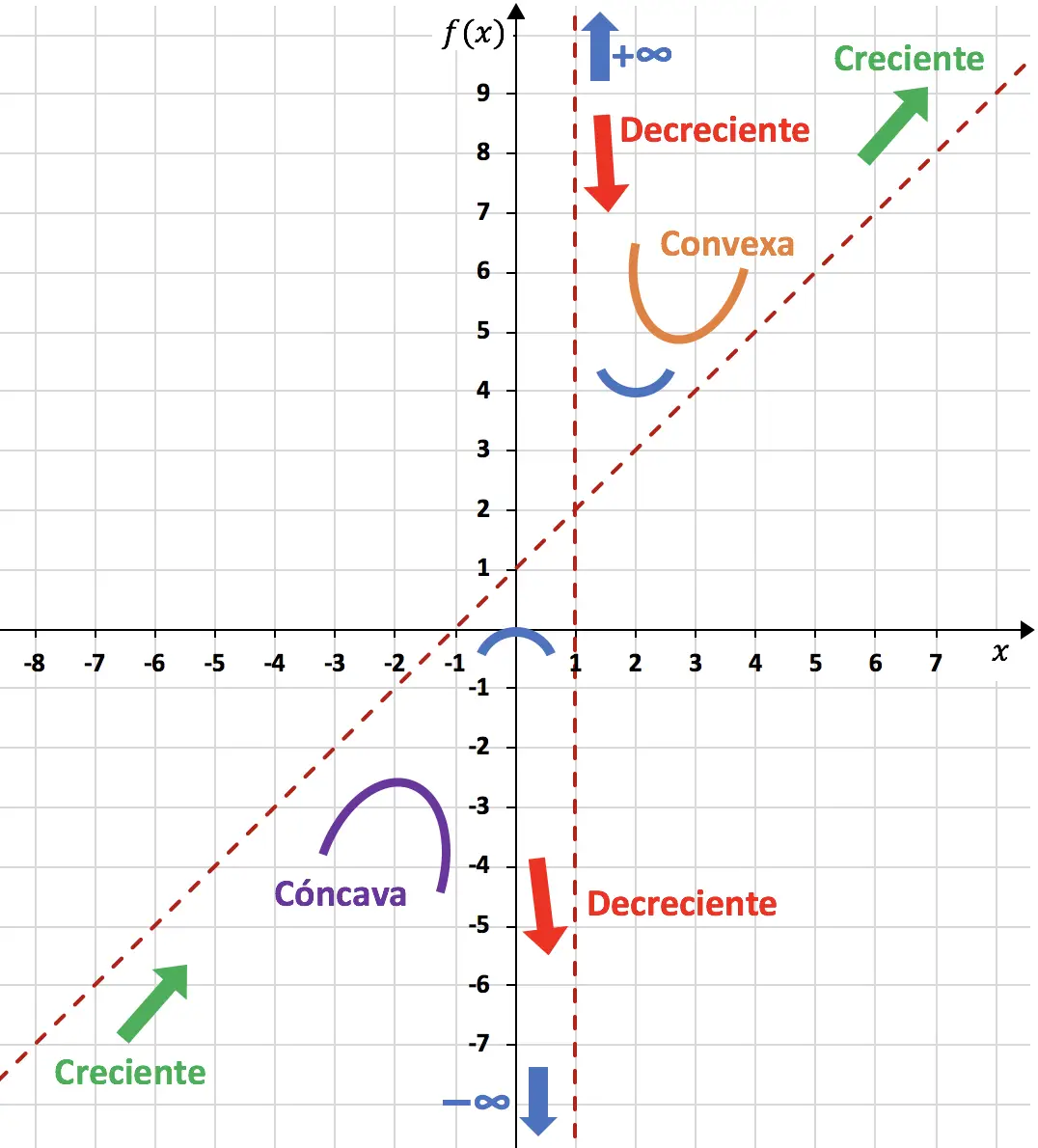
وبالتالي فإن الوظيفة الممثلة على الرسم البياني تبدو كما يلي:
تمارين محلولة لتمثيل الوظائف
التمرين 1
ارسم بيانيًا الدالة متعددة الحدود التالية:
![]()
أول شيء يجب فعله هو حساب مجال تعريف الدالة. هذه دالة متعددة الحدود، لذا يتكون المجال من أرقام حقيقية فقط:
![]()
لإيجاد نقطة التقاطع مع المحور X، نحل
![]()
![]()
![]()
هذه معادلة درجة أكبر من 2. لذلك، نقوم بتحليل المعادلة:
![]()
لذا فإن x=-1 هو الحل. ونقوم بحساب الحلول الأخرى من خلال حل المعادلة التربيعية الناتجة:
![Rendered by QuickLaTeX.com \begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e79a2a2f6650c4095c0dca52188c40c3_l3.png)
وبالتالي فإن نقاط التقاطع مع المحور X هي:
![]()
و
![]()
ولإيجاد نقطة التقاطع مع المحور Y نحسب
![]()
بما أن x دائمًا 0 على المحور Y:
![]()
وبالتالي فإن نقطة التقاطع مع المحور Y هي:
![]()
لمعرفة ما إذا كانت الدالة لها خطوط تقارب رأسية، علينا حساب نهاية الدالة عند نقاط لا تنتمي إلى المجال. في هذه الحالة، يتضمن المجال جميع الأعداد الحقيقية. وبالتالي فإن الدالة ليس لها خط تقارب رأسي.
ومن ناحية أخرى، فإن الخط المقارب الأفقي للدالة سيكون نتيجة النهاية اللانهائية للدالة. حتى الآن:
![]()
النهاية اللانهائية للدالة أعطتنا +∞، لذا فإن الدالة ليس لها خط تقارب أفقي.
نحن الآن نحسب الخط المقارب المائل. الخطوط المقاربة المائلة هي من النموذج
![]()
و
![]()
ويتم حسابها بالصيغة التالية:
![]()
![]()
النهاية أعطتنا +∞، لذا فإن الدالة ليس لها خط تقارب مائل.
لدراسة رتابة الدالة، يجب علينا أولاً حساب مشتقتها:
![]()
الآن نجعل المشتق يساوي 0 ونحل المعادلة:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d23e2b378508baca9f51117fc8767e90_l3.png)
نحن نمثل الآن على خط الأعداد جميع النقاط المفردة التي تم الحصول عليها، أي النقاط التي لا تنتمي إلى المجال (في هذه الحالة، جميعها تنتمي) وتلك التي تلغي المشتقة (x=0 وx =2) :

ونحسب إشارة المشتقة في كل فترة لنعرف ما إذا كانت الدالة تزيد أم تنقص. لذلك نأخذ نقطة في كل فترة (وليس النقاط المفردة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند هذه النقطة:
![]()
![]()
![]()

إذا كانت المشتقة موجبة فهذا يعني أن الدالة تتزايد، وإذا كانت المشتقة سالبة فهذا يعني أن الدالة تتناقص. وبالتالي فإن فترات النمو والانخفاض هي:
نمو:
![]()
ينقص:
![]()
تنتقل الدالة من التزايد إلى التناقص عند x=0، لذا فإن x=0 هو الحد الأقصى للدالة. وتنتقل الدالة من التناقص إلى الزيادة عند x=2، لذا فإن x=2 هو الحد الأدنى للدالة.
أخيرًا، نعوض الحدود القصوى الموجودة في الدالة الأصلية لإيجاد إحداثيات Y للنقاط:
![]()
![]()
وبالتالي فإن الحدود النسبية للوظيفة هي:
الحد الأقصى على النقطة
![]()
الحد الأدنى للنقطة
![]()
لدراسة انحناء الدالة نحسب مشتقتها الثانية:
![]()
الآن نجعل المشتقة الثانية تساوي 0 ونحل المعادلة:
![]()
![]()
![]()
![]()
نحن نمثل على الخط جميع النقاط المفردة التي تم العثور عليها، أي النقاط التي لا تنتمي إلى المجال (في هذه الحالة جميعها تنتمي) وتلك التي تلغي المشتقة (x=1):

والآن نحسب إشارة المشتقة الثانية في كل فترة لنعرف ما إذا كانت الدالة مقعرة أم محدبة. لذلك نأخذ نقطة في كل فترة (وليس النقاط المفردة أبدًا) وننظر إلى الإشارة التي يحملها المشتق الثاني عند هذه النقطة:
![]()
![]()

إذا كانت المشتقة الثانية موجبة، فهذا يعني أن الدالة محدبة.
![]()
وإذا كانت المشتقة الثانية سالبة فهذا يعني أن الدالة مقعرة
![]()
. وبالتالي فإن فترات التقعر والتحدب هي:
محدب
![]()
:
![]()
مقعر
![]()
:
![]()
بالإضافة إلى ذلك، تتغير الدالة من مقعرة إلى محدبة عند x=1، لذا فإن x=1 هي نقطة انقلاب للدالة.
أخيرًا، نستبدل نقاط الانعطاف الموجودة في الدالة الأصلية لإيجاد الإحداثي Y للنقاط:
![]()
وبالتالي فإن نقاط التحول في الوظيفة هي:
نقطة تحول:
![]()
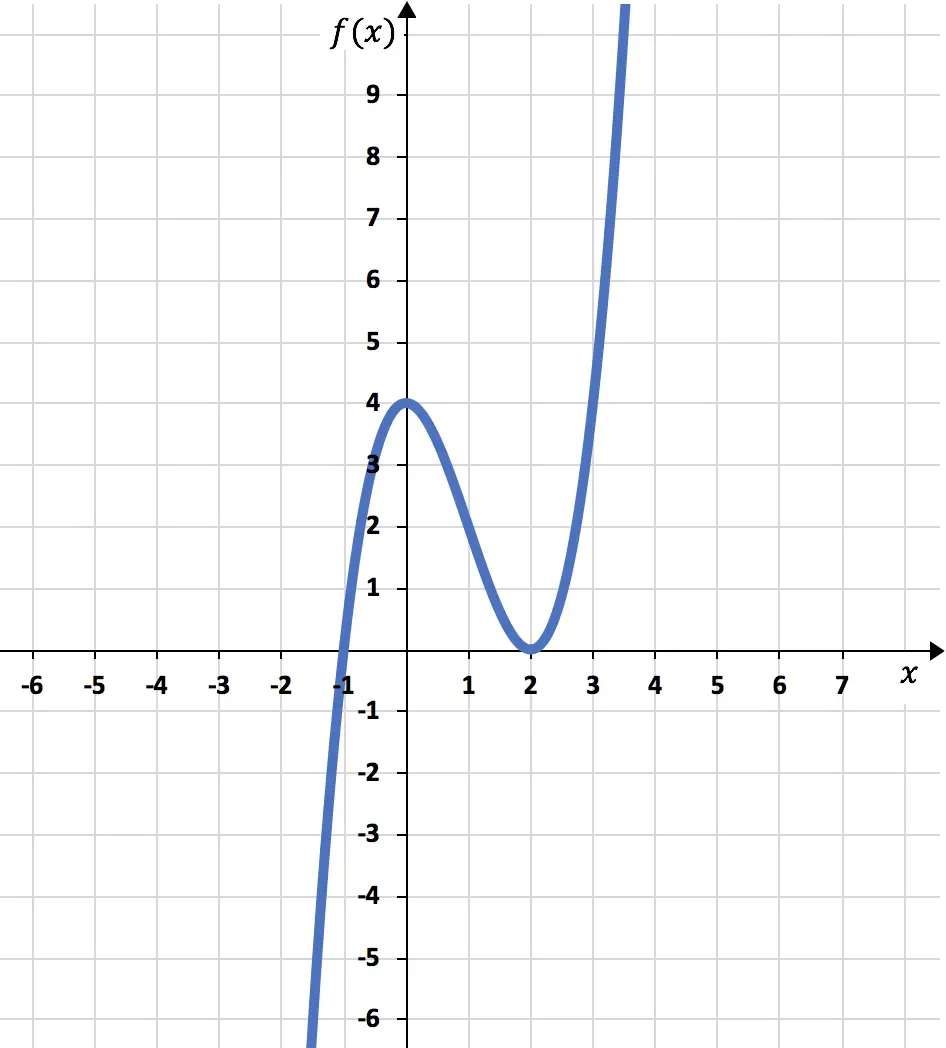
أخيرًا، استنادًا إلى جميع المعلومات التي حسبناها، نرسم الدالة رسمًا بيانيًا:
تمرين 2
ارسم بيانيًا الدالة العقلانية التالية:
![]()
لإيجاد مجال الدالة، نساوي المقام. أحضر الكسر إلى الصفر وحل المعادلة الناتجة:
![]()
![]()
![]()
![]()
![]()
ثانيًا، نحدد عتبات الدالة حيث يكون المحور السيني مساويًا للتعبير الجبري للدالة. فُولاَذ:
![]()
![]()
![]()
![]()
![]()
![]()
لا يوجد جذر تربيعي لعدد سالب. ولذلك، الدالة لا تتقاطع مع المحور X.
ولإيجاد نقطة التقاطع مع محور الكمبيوتر، نقيم الدالة عند x=0.
![]()
وبالتالي فإن نقطة التقاطع مع المحور Y هي:
![]()
لمعرفة ما إذا كانت الدالة لها خطوط مقاربة رأسية، نحتاج إلى حساب نهاية الدالة عند نقاط لا تنتمي إلى المجال (في هذه الحالة x=-1 وx=+1). وإذا كانت النتيجة لا نهائية، فهو خط مقارب عمودي. حتى الآن:
![]()
بما أن نهاية الدالة عندما تقترب x من -1 تعطي ما لا نهاية، فإن x=-1 هو خط مقارب رأسي.
نحسب الحدود الجانبية للخط المقارب x=-1 عن طريق استبدال رقم قريب جدًا منه في الدالة:
![]()
![]()
الآن دعونا نرى ما إذا كان x=+1 خطًا مقاربًا رأسيًا:
![]()
بما أن نهاية الدالة عندما تقترب x من +1 تعطي ما لا نهاية، فإن x=+1 هو خط مقارب رأسي.
نحسب الحدود الجانبية للخط المقارب x=1 عن طريق استبدال رقم قريب جدًا منه في الدالة:
![]()
![]()
ومن ناحية أخرى، فإن الخط المقارب الأفقي للدالة سيكون نتيجة النهاية اللانهائية للدالة. حتى الآن:
![]()
الحد اللانهائي للدالة أعطانا 1، لذا فإن الدالة لها خط تقارب أفقي عند y=1.
بما أن الدالة لها خط تقارب أفقي، فلن يكون لها خط تقارب مائل.
نقوم بتفريق الدالة ثم دراسة فترات النمو والتناقص:
![]()
![]()
الآن نجعل المشتق يساوي 0 ونحل المعادلة:
![]()
![]()
![]()
![]()
![]()
نمثل على الخط جميع النقاط الحرجة المحسوبة، وهي النقاط التي لا تنتمي إلى المجال (x=-1 وx=+1) وتلك التي تلغي المشتقة (x=0):

ونحسب إشارة المشتقة في كل فترة لنعرف ما إذا كانت الدالة تزيد أم تنقص. لذلك نأخذ نقطة في كل فترة (وليس النقاط المفردة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند هذه النقطة:
![]()
![]()
![]()
![]()
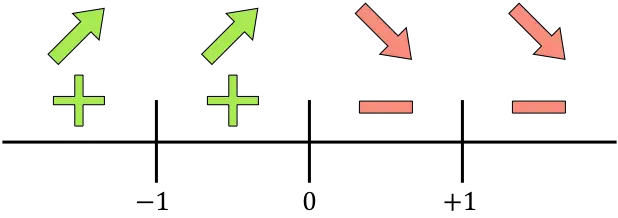
تزداد الدالة عندما تكون المشتقة موجبة وتتناقص الدالة عندما تكون الدالة سالبة:
نمو:
![]()
ينقص:
![]()
تنتقل الدالة من الزيادة إلى التناقص عند x=0، لذا فإن x=0 هو الحد الأقصى المحلي للدالة.
نعوض بالقيمة القصوى الموجودة في الدالة الأصلية لإيجاد الإحداثي Y للنقطة:
![]()
وبالتالي فإن الحدود النسبية للوظيفة هي:
الحد الأقصى على النقطة
![]()
لدراسة انحناء الدالة نحسب مشتقتها الثانية:
![f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}” title=”Rendered by QuickLaTeX.com”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-802852beb818dd5a0dce2f30374f3a88_l3.png) جميع المصطلحات لديها
جميع المصطلحات لديها
![]()
، يمكننا بالتالي تبسيط الكسر:
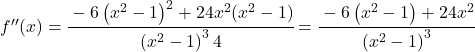
![]()
الآن نجعل المشتقة الثانية تساوي 0 ونحل المعادلة:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
لا يوجد جذر تربيعي لعدد سالب. لذلك ليس هناك أي نقطة تتطابق
![]()
الآن نمثل على الخط جميع النقاط المفردة التي تم العثور عليها، أي النقاط التي لا تنتمي إلى المجال (x=-1 وx=+1) وتلك التي تلغي المشتقة الثانية (في هذه الحالة لا يوجد أي):
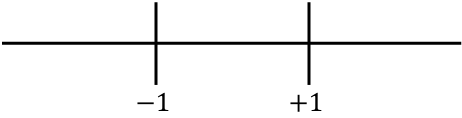
ونحسب إشارة المشتقة الثانية في كل فترة لنعرف ما إذا كانت الدالة مقعرة أم محدبة. لذلك نأخذ نقطة في كل فترة (وليس النقاط المفردة أبدًا) وننظر إلى الإشارة التي يحملها المشتق الثاني عند هذه النقطة:
![]()
![]()
![]()

إذا كانت المشتقة الثانية موجبة، فهذا يعني أن الدالة محدبة.
![]()
وإذا كانت المشتقة الثانية سالبة فهذا يعني أن الدالة مقعرة
![]()
. وبالتالي فإن فترات التقعر والتحدب هي:
محدب
![]()
:
![]()
مقعر
![]()
:
![]()
ومع ذلك، على الرغم من وجود تغيير في الانحناء عند x=-1 وعند x=1، إلا أن هذه ليست نقاط انعطاف. لأنها لا تنتمي إلى مجال الوظيفة.
وأخيرًا، نرسم الدالة بيانيًا باستخدام جميع الحسابات التي تم إجراؤها:
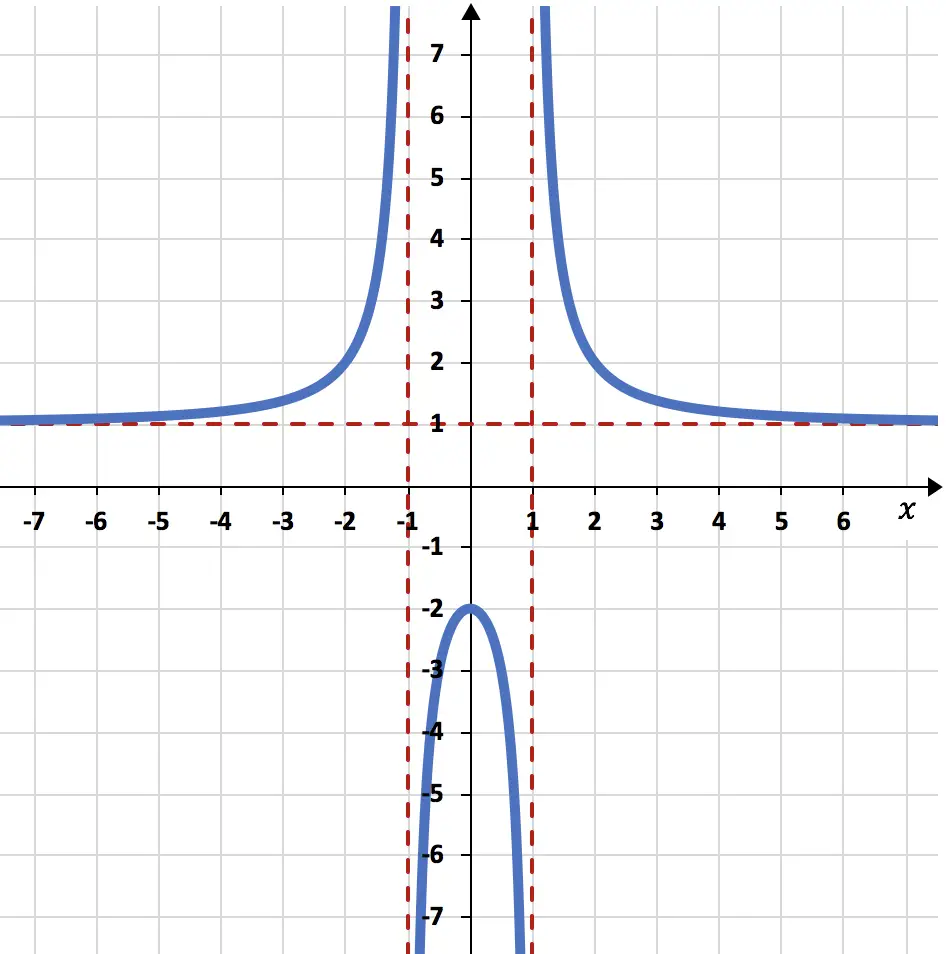
التمرين 3
ارسم الدالة المنطقية التالية على الرسم البياني:
![]()
هذه دالة عقلانية، لذا نحتاج إلى جعل المقام يساوي 0 لمعرفة الأرقام التي لا تنتمي إلى مجال الدالة:
![]()
![]()
![]()
![]()
![]()
لإيجاد نقطة التقاطع مع المحور X، نحل
![]()
نظرًا لأن الدالة دائمًا لها قيمة 0 على المحور X:
![]()
![]()
![]()
![]()
![]()
وبالتالي فإن نقطة التقاطع مع المحور X هي:
![]()
ولإيجاد نقطة التقاطع مع المحور Y نحسب
![]()
بما أن x دائمًا 0 على المحور Y:
![]()
وبالتالي فإن نقطة التقاطع مع المحور Y هي:
![]()
في هذه الحالة، تتزامن نقطة التقاطع مع المحور X مع نقطة التقاطع مع المحور Y، حيث تمر الدالة عبر أصل الإحداثيات.
لمعرفة ما إذا كانت الدالة لها خطوط مقاربة رأسية، نحتاج إلى حساب نهاية الدالة عند نقاط لا تنتمي إلى المجال (في هذه الحالة x=-2 وx=+2). وإذا كانت النتيجة لا نهائية، فهو خط مقارب عمودي. حتى الآن:
![]()
بما أن نهاية الدالة عندما تقترب x من -2 تعطي ما لا نهاية، فإن x=-2 هو خط مقارب رأسي.
نحسب الحدود الجانبية للخط المقارب x=-2 عن طريق استبدال رقم قريب جدًا منه في الدالة:
![]()
![]()
الآن دعونا نرى ما إذا كان x=+2 خطًا مقاربًا رأسيًا:
![]()
بما أن نهاية الدالة عندما تقترب x من +2 تعطي ما لا نهاية، فإن x=+2 هو خط مقارب رأسي.
نحسب الحدود الجانبية للخط المقارب x=2 عن طريق استبدال رقم قريب جدًا منه في الدالة:
![]()
![]()
ومن ناحية أخرى، فإن الخط المقارب الأفقي للدالة سيكون نتيجة النهاية اللانهائية للدالة. حتى الآن:
![]()
النهاية اللانهائية للدالة أعطتنا +∞، لذا فإن الدالة ليس لها خط تقارب أفقي.
نحن الآن نحسب الخط المقارب المائل. الخطوط المقاربة المائلة هي من النموذج
![]()
و
![]()
ويتم حسابها بالصيغة التالية:
![]()
![]()
![]()
بمجرد أن نعرف ميل الخط المقارب المائل، نحدد التقاطع باستخدام الصيغة التالية:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-de4326a40acf34b64a28c9da8250bf00_l3.png)
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13478ac6f6fac958ec8b2a714c28bc3d_l3.png)
لكننا حصلنا على عدم التعيين ∞ – ∞. ولذلك فمن الضروري اختزال الشروط إلى قاسم مشترك. للقيام بذلك، نضرب ونقسم x على مقام الكسر:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e939b43a3405ba644d4b60bb4bacadb_l3.png)
![]()
![]()
باختصار الخط المقارب المائل هو:
![]()
![]()
![]()
لدراسة رتابة الدالة، يجب علينا أولاً حساب مشتقتها:
![]()
![]()
الآن نجعل المشتق يساوي 0 ونحل المعادلة:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc1f64cdcd293da4fee1ef02fff9a588_l3.png)
نمثل الآن على الخط جميع النقاط المفردة التي تم العثور عليها، أي النقاط التي لا تنتمي إلى المجال (x=-2 وx=+2) وتلك التي تلغي المشتقة (x=0، x=-) 3.46 و س= +3.46):

ونحسب إشارة المشتقة في كل فترة لنعرف ما إذا كانت الدالة تزيد أم تنقص. لذلك نأخذ نقطة في كل فترة (وليس النقاط المفردة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند هذه النقطة:
![]()
![]()
![]()
![]()
![]()
![]()
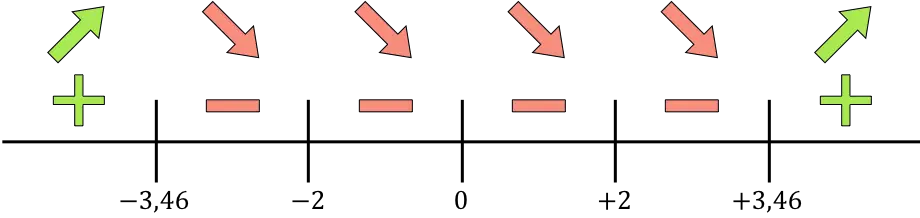
إذا كانت المشتقة موجبة فهذا يعني أن الدالة تتزايد، وإذا كانت المشتقة سالبة فهذا يعني أن الدالة تتناقص. وبالتالي فإن فترات النمو والانخفاض هي:
نمو:
![]()
ينقص:
![]()
تنتقل الدالة من الزيادة إلى التناقص عند x=-3.46، لذا فإن x=-3.46 هي القيمة القصوى للدالة. وتنتقل الدالة من التناقص إلى الزيادة عند x=3.46، لذا فإن x=3.46 هو الحد الأدنى للدالة.
نحدد إحداثيات Y للنهايات النسبية:
![]()
![]()
وبالتالي فإن الحدود النسبية للوظيفة هي:
الحد الأقصى على النقطة
![]()
الحد الأدنى للنقطة
![]()
لدراسة انحناء الدالة نحسب المشتقة الثانية للدالة:



![]()
![]()
![]()
![]()
الآن نجعل المشتقة الثانية تساوي 0 ونحل المعادلة:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]()
لا يوجد حل لأنه لا يوجد جذر سلبي لعدد حقيقي.
نمثل الآن على الخط جميع النقاط المفردة التي تم العثور عليها، أي النقاط التي لا تنتمي إلى المجال (x=-2 وx=+2) وتلك التي تلغي المشتقة الثانية (x=0):

ونحسب إشارة المشتقة الثانية في كل فترة لنعرف ما إذا كانت الدالة مقعرة أم محدبة. لذلك نأخذ نقطة في كل فترة (وليس النقاط المفردة أبدًا) وننظر إلى الإشارة التي يحملها المشتق الثاني عند هذه النقطة:
![]()
![]()
![]()
![]()

إذا كانت المشتقة الثانية موجبة، فهذا يعني أن الدالة محدبة.
![]()
وإذا كانت المشتقة الثانية سالبة فهذا يعني أن الدالة مقعرة
![]()
. وبالتالي فإن فترات التقعر والتحدب هي:
محدب
![]()
:
![]()
مقعر
![]()
:
![]()
ومع ذلك، على الرغم من وجود تغيير في الانحناء عند x=-2 وx=+2، إلا أن هذه ليست نقاط انعطاف. لأن x=-2 وx=+2 لا ينتميان إلى مجال الوظيفة. من ناحية أخرى، عند x=0 هناك تغيير في الانحناء (تنتقل الدالة من محدب إلى مقعر) وهذا ينتمي إلى الدالة، لذا فإن x=0 هي نقطة انقلاب.
نستبدل نقاط الانعطاف الموجودة في الدالة الأصلية لإيجاد الإحداثيات الأخرى لنقطة الانعطاف:
![]()
وبالتالي فإن نقاط التحول في الوظيفة هي:
نقطة تحول:
![]()
أخيرًا، بناءً على جميع المعلومات التي حسبناها، نمثل الدالة:
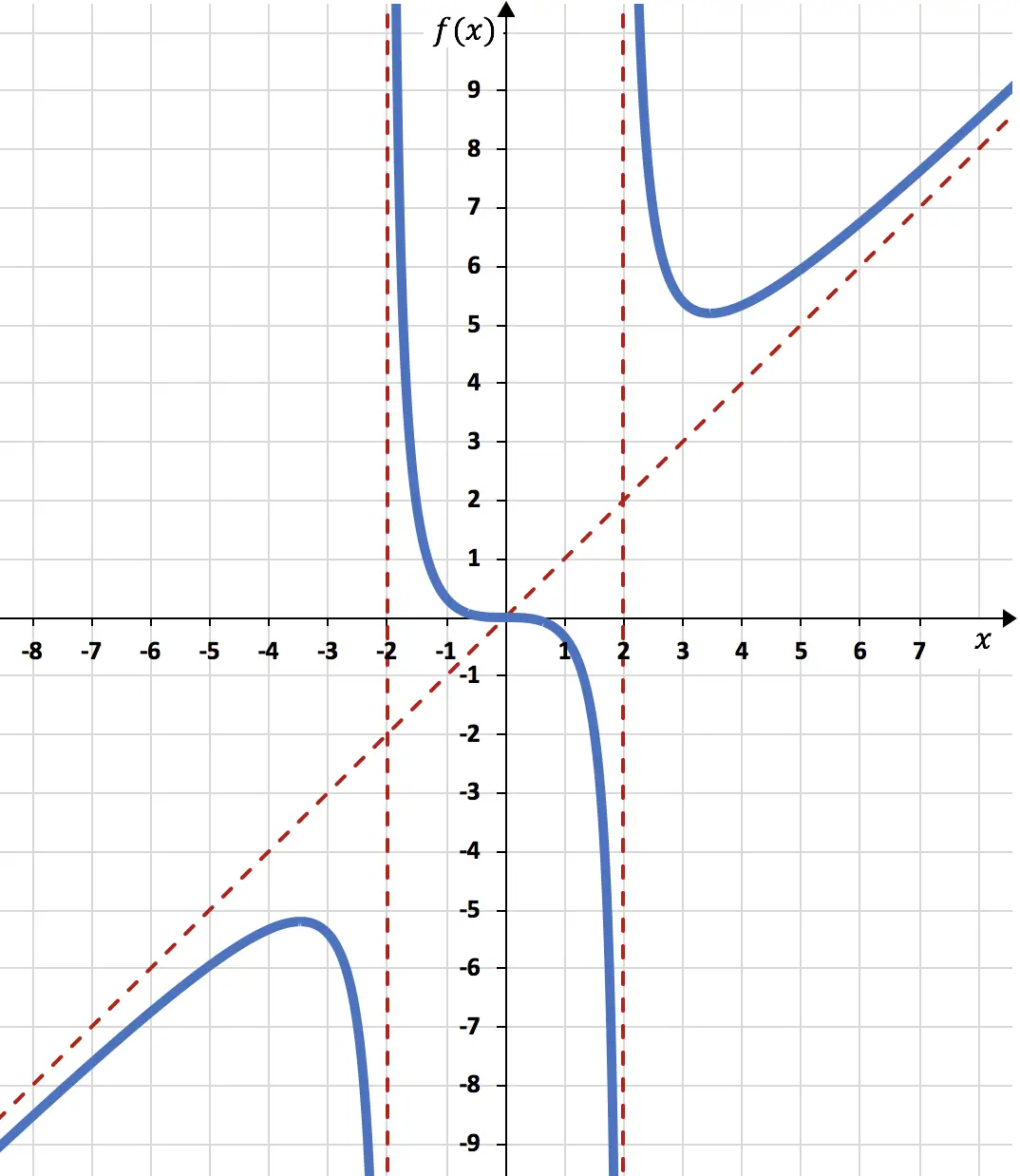
تعليق: لاحظ أن الدالة تعبر الخط المقارب المائل عند النقطة
![]()
في الواقع، تحدد الخطوط المقاربة المائلة قبل كل شيء سلوك الوظيفة عندما تميل x نحو +∞ و -∞، في الواقع، لا تعبر الدالة أبدًا الخط المقارب المائل إلى يمين الرسم البياني (x→+∞) وإلى يسار الرسم البياني (x→-∞). ومع ذلك، من النادر جدًا أن تعبر الدالة الخط المقارب المائل في المنتصف، فهي حالة خاصة جدًا.