في هذه المقالة، سوف تتعلم كيفية دراسة اشتقاق دالة، أي ما إذا كانت الدالة قابلة للاشتقاق أم لا. بالإضافة إلى ذلك، سوف نرى العلاقة بين التفاضل واستمرارية الوظيفة. وأخيرًا، سندرس اشتقاق دالة متعددة التعريف.
التفاضل واستمرارية الوظيفة
ترتبط الاستمرارية والتمايز للدالة عند نقطة ما بما يلي:
- إذا كانت الدالة قابلة للاشتقاق عند نقطة ما، فإن الدالة متصلة عند تلك النقطة.
- إذا كانت الدالة غير متصلة عند نقطة ما، فهي أيضًا غير قابلة للاشتقاق عند تلك النقطة.
ومع ذلك، فإن عكس هذه النظرية خاطئ: فمجرد أن الدالة متصلة عند نقطة ما لا يعني أنها قابلة للاشتقاق دائمًا عند تلك النقطة.
يمكنك أيضًا معرفة ما إذا كانت الدالة قابلة للاشتقاق عند نقطة ما من تمثيلها الرسومي أم لا:
- إذا كانت نقطة ناعمة، تكون الدالة قابلة للاشتقاق عند هذه النقطة.
- إذا كانت نقطة زاوية، تكون الدالة متصلة ولكنها غير قابلة للاشتقاق عند هذه النقطة.
نقطة التجانس عند x=0:
دالة مستمرة وقابلة للتفاضل في هذه المرحلة.
النقطة الزاوية عند x=2:
وظيفة مستمرة ولكن غير قابلة للتمييز في هذه المرحلة.
تفاضل دالة متعددة التعريف
بمجرد أن نعرف العلاقة بين الاستمرارية وقابلية تفاضل الدالة، سنرى كيفية دراسة قابلية تفاضل دالة محددة.
يمكنك معرفة ما إذا كانت الدالة المتعددة التعريف قابلة للاشتقاق عند نقطة ما عن طريق حساب المشتقات الجانبية عند تلك النقطة:
- إذا كانت المشتقات الجانبية عند نقطة ما غير متساوية، فإن الدالة غير قابلة للاشتقاق عند تلك النقطة:
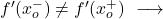
ولا يجوز خصمه في
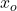
- إذا تطابقت المشتقات الجانبية عند نقطة ما، تكون الدالة قابلة للاشتقاق عند تلك النقطة:
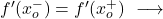
نعم يجوز التفريق فيه
ملاحظة: لكي تكون الدالة قابلة للاشتقاق عند نقطة ما، يجب أن تكون الدالة متصلة عند تلك النقطة. ولذلك، قبل حساب المشتقات الجانبية، علينا التأكد من أن الدالة متصلة عند تلك النقطة. إذا كنت لا تعرف كيف تتم دراسة الاستمرارية عند نقطة ما، يمكنك الاطلاع على كيفية ذلك في الرابط التالي:
➤ انظر: استمرارية الدالة عند نقطة ما
الآن دعونا نرى مثالاً لكيفية حساب مشتقة دالة محددة عند نقطة ما:
- ادرس الاستمرارية والتمايز للدالة التالية المحددة عند النقطة x=2:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
وظائف الجزأين متصلة في فترات كل منها، ولكن من الضروري معرفة ما إذا كانت الوظيفة مستمرة عند النقطة الحرجة x=2. للقيام بذلك، نحل الحدود الجانبية للدالة عند النقطة:
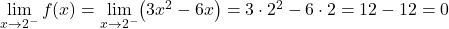
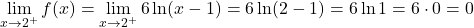
الحدود الجانبية عند النقطة الحرجة أعطتنا نفس النتيجة، وبالتالي فإن الدالة متصلة عند النقطة x=2.
بمجرد أن نعرف أن الدالة متصلة عند x=2، سندرس اشتقاق الدالة عند تلك النقطة. للقيام بذلك، نحسب المشتقات الجانبية للدالة المحددة بالقطع:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
نقوم الآن بتقييم كل مشتق جانبي عند النقطة الحرجة:
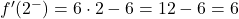
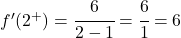
أعطتنا المشتقتان الجانبيتان نفس النتيجة، وبالتالي تكون الدالة قابلة للاشتقاق عند x=2 وقيمة المشتقة هي 6:
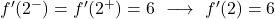
من ناحية أخرى، إذا أعطتنا المشتقات الجانبية نتيجة مختلفة، فهذا يعني أن الدالة غير قابلة للاشتقاق عند x=2. بعبارة أخرى، المشتقة لن تكون موجودة عند هذه النقطة.
أخيرًا، تذكر فقط أن هذا الإجراء صالح أيضًا لدراسة قابلية تفاضل دالة القيمة المطلقة، حيث يمكن أيضًا تعريف دوال القيمة المطلقة. يمكنك معرفة كيفية تحويل دالة القيمة المطلقة إلى أجزاء هنا:
➤ انظر: كيفية تعريف دالة متعددة القيمة ذات قيمة مطلقة
تمارين محلولة على تفاضل الدالة
التمرين 1
دراسة الاستمرارية والتمايز للدالة المتعددة التعريف التالية:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
دوال الجزأين متصلة، لكن يجب أن نرى ما إذا كانت الدالة مستمرة عند النقطة الحرجة x=1. للقيام بذلك نحل الحدود الجانبية للدالة عند النقطة:
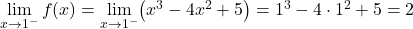
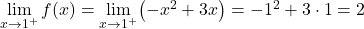
النهايتان الجانبيتان عند النقطة الحرجة تعطيان نفس النتيجة، وبالتالي تكون الدالة متصلة عند x=1.
بمجرد أن عرفنا أن الدالة متصلة عند النقطة الحرجة، سندرس ما إذا كانت قابلة للاشتقاق عند نفس النقطة. لذلك نحسب المشتقات الجانبية:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
ونقوم بتقييم المشتقتين الجانبيتين عند x=1؛
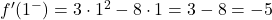
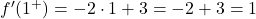
المشتقات الجانبية لا تتطابق عند النقطة x=1 لذا فإن الدالة غير قابلة للاشتقاق عند هذه النقطة.
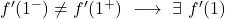
تمرين 2
تحليل التمايز والاستمرارية للوظيفة التالية المحددة في الأقسام:
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
انظر الحل
دوال القسمين متصلة في فتراتها، ولكن من الضروري أيضًا معرفة ما إذا كانت الدالة مستمرة عند النقطة الحرجة لتغيير التعريف x=1. لذلك نحدد الحدود الجانبية للدالة عند هذه النقطة:
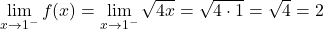
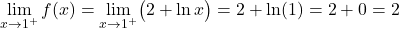
النهايتان الجانبيتان عند النقطة الحرجة تعطيان نفس النتيجة، وبالتالي تكون الدالة متصلة عند x=1.
والآن ندرس ما إذا كانت الدالة قابلة للاشتقاق عند هذه النقطة عن طريق حساب المشتقات الجانبية:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
نقوم بتقييم المشتقتين الجانبيتين عند x=1:
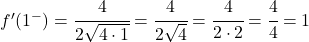
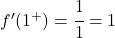
المشتقات الجانبية متساوية، وبالتالي تكون الدالة قابلة للاشتقاق عند x=1 وقيمة المشتقة هي 1.
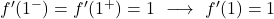
التمرين 3
حدد ما إذا كانت الدالة المتعددة التعريف التالية متصلة وقابلة للتفاضل في مجالها بالكامل:
*** QuickLaTeX cannot compile formula:
\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+1 & \text{si} & x\leq -1 \\[2ex] 2x+2 & \text{ si} & -1<div class="wp-block-otfm-box-spoiler-start otfm-sp__wrapper otfm-sp__box js-otfm-sp-box__closed otfm-sp__E6F9EF" role="button" tabindex="0" aria- expanded="false" data-otfm-spc="#E6F9EF" style="text-align:center"><div class="otfm-sp__title"> <strong>View solution</strong></div>< /div> The functions of all three parts are continuous, but we still need to check if the function is continuous at critical points. We therefore first check the continuity of the function at the point x=-1 by solving the lateral limits at this point:
*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: ...="wp-block-otfm-box-spoiler-start otfm-sp__
Missing { inserted.
leading text: ...ox-spoiler-start otfm-sp__wrapper otfm-sp__
Missing { inserted.
leading text: ...m-sp__wrapper otfm-sp__box js-otfm-sp-box__
Missing { inserted.
leading text: ...fm-sp__box js-otfm-sp-box__closed otfm-sp__
You can't use `macro parameter character #' in math mode.
leading text: ...="0" aria-expanded="false" data-otfm-spc="#
Missing { inserted.
leading text: ...e="text-align:center"><div class="otfm-sp__
Please use \mathaccent for accents in math mode.
leading text: ...g></div></div> The functions of the three parts
Please use \mathaccent for accents in math mode.
leading text: ...are continuous, but we still need to see
\lim\limits_{x\to -1^-} f(x) = \lim\limits_{x\to -1^-} \bigl(x^2+2x+1\bigr) = (-1)^ 2+2(-1)+1 =0 \lim\limits_{x\to -1^+} f(x) = \lim\limits_{x\to -1^+} \bigl(2x+2\bigr ) = 2(-1)+2=0
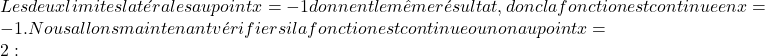
\lim\limits_{x\to 2^-} f(x) = \lim\limits_{x\to 2^-} \bigl(2x+2\bigr) = 2\cdot 2+2=4+2= 6 \lim\limits_{x\to 2^+} f(x) = \lim\limits_{x\to 2^+} \bigl( -x^2+8x\bigr) = -2^2+8\ كدوت 2 = -4+16=12
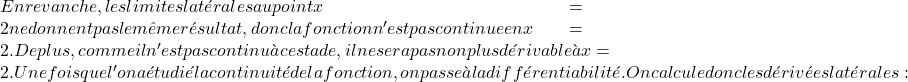
\displaystyle f'(x)= \left\{ \begin{array}{lcl} 2x+2 & \text{si} & x\leq -1 \\[2ex] 2 & \text{si} & -1
نحن نعلم بالفعل أن الدالة غير قابلة للاشتقاق عند x=2، لذا نحتاج فقط إلى دراسة ما إذا كانت الدالة قابلة للاشتقاق عند x=-1. للقيام بذلك، نقوم بتقييم المشتقتين الجانبيتين عند النقطة:
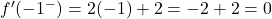
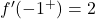
المشتقات الجانبية لا تتطابق عند النقطة x=-1، وبالتالي فإن الدالة غير قابلة للاشتقاق عند تلك النقطة.
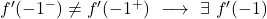
التمرين 4
احسب قيمة المعلمتين a وb بحيث تكون الدالة المتعددة التعريف التالية متصلة وقابلة للتمييز في مجالها بالكامل:
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
ومهما كانت قيم المجهولات فإن الدالة متصلة وقابلة للتفاضل في جميع النقاط باستثناء x=3 حيث يجب التحقق من استمراريتها وقابليتها للتفاضل.
لكي تكون الدالة متصلة عند نقطة ما، يجب أن تتطابق النهايتان الجانبيتان عند تلك النقطة. ولذلك، فإننا نقيم الحدود الجانبية عند النقطة الحرجة:
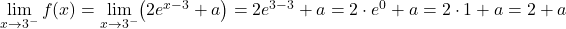
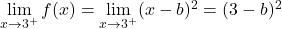
ولذلك يجب أن تكون القيمتان المتحصل عليهما من النهايات الجانبية متساويتين لكي تكون الدالة متصلة:
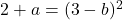
سنقوم الآن بتحليل التمايز عند النقطة x=3. نجد المشتقات الجانبية:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)
ونقوم بتقييم المشتقتين الجانبيتين عند النقطة الحرجة:
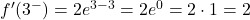
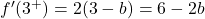
ولذلك، لكي تكون الدالة قابلة للاشتقاق عند x=3، يجب أن تكون القيم التي تم الحصول عليها من المشتقات الجانبية متساوية:
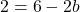
وبحل هذه المعادلة يمكننا إيجاد قيمة b:
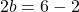
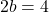
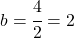
وأخيرًا، بمجرد معرفة قيمة المعلمة b، يمكننا حساب قيمة المعلمة a من خلال حل المعادلة التي حصلنا عليها سابقًا في الحدود الجانبية:
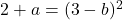
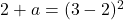
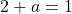
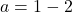
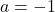


![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
![]()
![]()
![]()
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
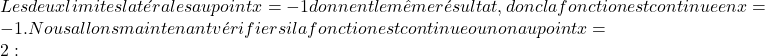
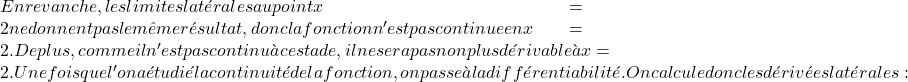
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)