معادلة خطية أو قطعية أو متماثلة للخط

ستجد هنا شرحًا لصيغة المعادلة الأساسية (أو القطاعية) للخط، والتي تسمى أيضًا المعادلة المتماثلة. بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتدرب على التمارين التي تم حلها. وحتى، ستجد كيفية حساب المعادلة الأساسية من المعادلة العامة (أو الضمنية) للخط.

ما هي المعادلة الأساسية أو القطاعية للخط؟

تذكر أن التعريف الرياضي للخط هو مجموعة من النقاط المتتالية الممثلة في نفس الاتجاه بدون منحنيات أو زوايا.

وبالتالي، فإن المعادلة الأساسية للخط ، والتي تسمى أيضًا المعادلة القطعية للخط ، هي طريقة للتعبير عن أي خط رياضيًا. وللقيام بذلك، يكفي معرفة نقاط التقاطع مع محاور إحداثيات الخط المذكور.

من ناحية أخرى، في الهندسة التحليلية، تسمى المعادلة الأساسية (أو القطاعية) للخط أيضًا المعادلة المتماثلة للخط .

صيغة المعادلة الأساسية أو القطاعية للخط

المعادلة القانونية أو القطعية للخط هي التعبير الجبري للخط الذي يمكن تحديده من خلال معرفة القيم التي يتقاطع فيها الخط مع المحور السيني والمحور الصادي.

إذا تقاطع خط مع المحاور الديكارتية في النقاط التالية:

نقطة التقاطع مع المحور X:

$(a,0)$

نقطة التقاطع مع المحور Y:

$(0,b)$

صيغة المعادلة الأساسية (أو القطاعية) للخط هي:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

تجدر الإشارة إلى أنه لا توجد معادلة قانونية (أو قطعية) للخط في أي من الحالات الثلاث التالية:

عندما يكون الخط عموديًا، فهذا يعني أنه موازٍ لمحور OY. لأن معادلة الخط العمودي هي
$x=k.$
عندما يكون الخط أفقيًا، فهذا يعني أنه موازٍ لمحور OX. لأن معادلة الخط الأفقي هي
$y=k.$
عندما يمر الخط عبر أصل الإحداثيات (النقطة
$(0,0)$

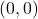
) ، لأنه سيكون لدينا بعد ذلك عدم تحديدين في معادلة الخط.

مثال لكيفية العثور على المعادلة الأساسية أو القطاعية للخط

لكي تفهم المفهوم بشكل أفضل، سنحل مسألة معادلة قطعية (أو أساسية) للخط:

أوجد المعادلة القانونية أو القطعية للخط الذي يمر بالنقطتين التاليتين:

$A(0,4) \qquad \qquad B(-2,0)$

وفي هذه الحالة فإن التصريح لا يعطينا نقطتين، بل نقطتي التقاطع مع المحورين.

نقطة تقاطع الخط مع المحور X :

$(-2,0)$

نقطة تقاطع الخط مع المحور Y:

$(0,4)$

لذا، بما أننا نعرف بالفعل نقطتي التقاطع مع المحورين، نحتاج فقط إلى تطبيق صيغة المعادلة الأساسية أو القطاعية للخط:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

وأخيرًا، نعوض بقيمة المعلمات

$a$

$b$

في الصيغة:

$\cfrac{\bm{x}}{\bm{-2}}\bm{+} \cfrac{\bm{y}}{\bm{4}}\bm{= 1}$

أنت تعرف الآن ما هي المعادلة الأساسية (أو القطاعية) للخط. ومع ذلك، يجب أن تعلم أن هناك طرقًا أخرى للتعبير عن خط مستقيم، ومن بينها تبرز المعادلة الصريحة . من الصعب فهم هذا النوع من المعادلات الخطية بشكل كامل، لذلك قمنا بشرح كل شيء عنه بالتفصيل في الصفحة المرتبطة.

احسب المعادلة الأساسية أو القطاعية للخط من معادلته العامة

لقد رأينا للتو طريقة لتحديد المعادلة الأساسية أو القطعية للخط، ولكن هناك أيضًا طرقًا أخرى:

يمكن الحصول على المعادلة الأساسية أو القطاعية للخط من المعادلة العامة (أو الضمنية) لنفس الخط:

$Ax+By+C=0$

أولاً، نغير الجوانب عند المعامل C:

$Ax+By=-C$

بعد ذلك، نقسم المعادلة بأكملها على قيمة المعلمة المتغيرة C:

$\cfrac{Ax+By}{-C}=\cfrac{-C}{-C}$

$\cfrac{Ax}{-C}+\cfrac{By}{-C}=1$

ومن خلال خصائص الكسور، نصل إلى صيغة المعادلة القانونية أو القطعية للخط:

$\cfrac{x}{-\frac{C}{A}}+\cfrac{y}{-\frac{C}{B}}=1$

ويترتب على ذلك من هذه الصيغة أن المصطلحات

$a$

$b$

من المعادلة الأساسية للخط تعادل التعبيرات التالية:

$a= -\cfrac{C}{A} \qquad \qquad b= -\cfrac{C}{B}$

حل مسائل المعادلة القانونية أو القطعية للخط

التمرين 1

ما نقاط التقاطع مع محاور إحداثيات الخط التالي؟

$\cfrac{x}{3}+ \cfrac{y}{-1}= 1$

انظر الحل

يتم التعبير عن الخط الموجود في التمرين على شكل معادلة قانونية أو قطعية للخط، وصيغتها هي:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

وبالتالي فإن النقاط التي يتقاطع فيها الخط مع محاور الإحداثيات هي:

نقطة التقاطع مع المحور X:

$\bm{(3,0)}$

نقطة التقاطع مع المحور Y:

$\bm{(0,-1)}$

تمرين 2

ما هي المعادلة الأساسية أو القطاعية للخط البياني؟

انظر الحل

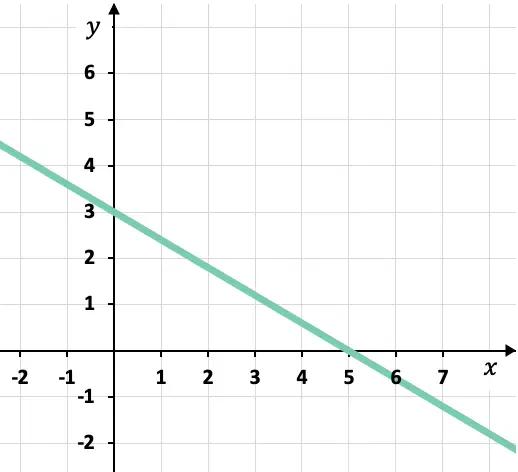
من الرسم البياني يمكننا معرفة النقاط التي يتقاطع فيها الخط مع محاور الإحداثيات:

نقطة تقاطع الخط مع المحور X :

$(5,0)$

نقطة تقاطع الخط مع المحور Y:

$(0,3)$

لذا، بمجرد أن نعرف بالفعل نقطتي التقاطع مع المحورين، نحتاج فقط إلى استخدام صيغة المعادلة الأساسية أو القطاعية للخط:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

وأخيرًا، نعوض بقيمة المعلمات

$a$

$b$

في الصيغة:

$\cfrac{\bm{x}}{\bm{5}}\bm{+} \cfrac{\bm{y}}{\bm{3}}\bm{= 1}$

التمرين 3

احسب المعادلة الأساسية أو القطاعية للخط الذي تحدده المعادلة العامة (أو الضمنية) التالية:

$3x-2y+6=0$

انظر الحل

للانتقال من معادلة عامة إلى معادلة قطعية، يجب علينا أولاً عزل الحد المستقل للمعادلة:

$3x-2y+6=0$

$3x-2y=-6$

ثانيًا، نقسم المعادلة بأكملها على المعامل الموجود على الجانب الأيمن من المعادلة:

$\cfrac{3x-2y}{-6}=\cfrac{-6}{-6}$

$\cfrac{3x}{-6}+\cfrac{-2y}{-6}=\cfrac{-6}{-6}$

التعبير أعلاه يعادل ما يلي:

$\cfrac{x}{\frac{-6}{3}}+\cfrac{y}{\frac{-6}{-2}}=1$

بحيث تكون المعادلة الأساسية أو القطعية أو المتماثلة للخط هي:

$\cfrac{\bm{x}}{\bm{-2}}\bm{+} \cfrac{\bm{y}}{\bm{3}}\bm{= 1}$

التمرين 4

تحديد المعادلة الأساسية أو القطاعية التي يكون متجه اتجاهها

$\vv{\text{v}}=(4,-3)$

ويمر عبر النقطة

$P(-1,5).$

انظر الحل

نقوم أولاً بالعثور بسهولة على المعادلة المستمرة للخط من متجه اتجاهه ونقطة تنتمي إلى الخط:

$\cfrac{x-P_1}{\text{v}_1} = \cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{4} = \cfrac{y-5}{-3}$

$\cfrac{x+1}{4} = \cfrac{y-5}{-3}$

لنحسب الآن المعادلة العامة للخط عن طريق ضرب الكسور بالعرض وتجميع الحدود الناتجة:

$-3(x+1) = 4(y-5)$

$-3x-3 = 4y-20$

$-3x-3 - 4y+20 =0$

$-3x - 4y+17 =0$

لذلك يكفي تحويل المعادلة العامة للخط إلى معادلة قانونية. للقيام بذلك، نقوم أولاً بحذف المصطلح المستقل من المعادلة:

$-3x - 4y=-17$

بعد ذلك، نقسم المعادلة بأكملها على المعامل الموجود على الجانب الأيمن من المعادلة:

$\cfrac{-3x - 4y}{-17}=\cfrac{-17}{-17}$

$\cfrac{-3x}{-17}+\cfrac{-4y}{-17}=\cfrac{-17}{-17}$

التعبير أعلاه يعادل ما يلي:

$\cfrac{x}{\frac{-17}{-3}}+\cfrac{y}{\frac{-17}{-4}}=1$

السالب مقسومًا على السالب يساوي الموجب:

$\cfrac{x}{\frac{17}{3}}+\cfrac{y}{\frac{17}{4}}=1$

لا يمكن تبسيط الكسور بشكل أكبر، وبالتالي فإن المعادلة الأساسية أو القطاعية أو المتماثلة للخط هي:

$\cfrac{\bm{x}}{\mathbf{\frac{17}{3}}}\bm{+} \cfrac{\bm{y}}{\mathbf{\frac{17}{4}}}\bm{= 1}$

ما هي المعادلة الأساسية أو القطاعية للخط؟

صيغة المعادلة الأساسية أو القطاعية للخط

مثال لكيفية العثور على المعادلة الأساسية أو القطاعية للخط

احسب المعادلة الأساسية أو القطاعية للخط من معادلته العامة

حل مسائل المعادلة القانونية أو القطعية للخط

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد