ستجد هنا كل ما يتعلق بالقطع الزائد: ما هو، وما هي عناصره المميزة، وكيفية العثور على معادلته، والأمثلة، والتدريبات المحلولة، وما إلى ذلك.
ما هو الغلو؟
القطع الزائد هو منحنى مفتوح ذو فرعين، التعريف الرياضي له هو كما يلي:
في الهندسة التحليلية، القطع الزائد هو موضع النقاط على المستوى الذي يستوفي الشرط التالي: القيمة المطلقة للفرق في المسافات بين أي نقطة من القطع الزائد ونقطتين ثابتتين (تسمى البؤر) يجب أن تكون ثابتة.
علاوة على ذلك، فإن قيمة طرح هاتين المسافتين تعادل دائمًا المسافة بين رأسي القطع الزائد.
![]()

أدناه سنرى ما يعنيه المعامل
![]()
من المبالغة.
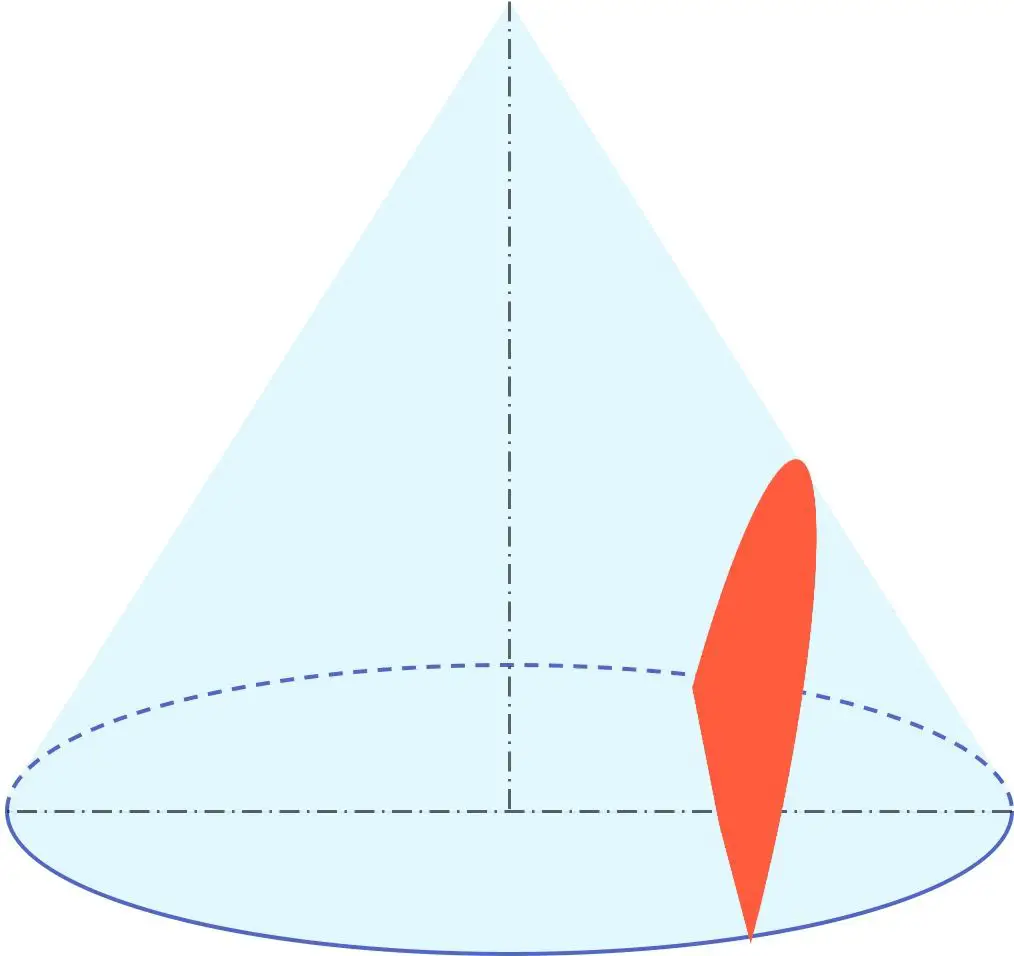
بالإضافة إلى ذلك، فإن القطع الزائد هو جزء من المجموعة الهندسية التي تسمى المخروطات إلى جانب المحيط والقطع الناقص والقطع المكافئ. ولذلك فإن القطع الزائد هو مقطع مخروطي، أو بمعنى آخر يمكن الحصول عليه من المخروط.
على وجه الخصوص، القطع الزائد هو نتيجة قسم المخروط بواسطة مستوى بزاوية أقل من الزاوية التي شكلها مولد المخروط بالنسبة إلى محور دورانه.
عناصر القطع الزائد
تعتمد خصائص القطع الزائد على ما يلي:
- البؤرتان : هاتان النقطتان الثابتتان المميزتان لكل قطع زائد (النقطتان F وF’ في الرسم البياني أدناه). القيمة المطلقة للفرق بين المسافات من أي نقطة القطع الزائد إلى كل بؤرة تكون ثابتة وتساوي

- المحور البؤري أو الرئيسي : هو الخط الذي يمر عبر بؤرتي القطع الزائد. وهو يتوافق مع محور تناظر الشكل الهندسي المذكور. ويسمى أيضًا المحور العرضي أو العرضي.
- المحور الثانوي : هو منصف القطعة FF’ (الخط الذي يمر بالنقطتين B و B’). بالإضافة إلى أنه خط متعامد مع محور البؤرة وهو محور آخر لتناظر القطع الزائد
- المركز (O) : هو نقطة تقاطع المحورين ونقطة منتصف الرأسين والبؤرتين. بما أن القطع الزائد له محورين للتماثل، فهو أيضًا مركز التماثل.
- القمم (A و A’) : هي نقاط تقاطع فروع القطع الزائد مع المحور البؤري.
- الأشعة المتجهة (R) : هي الأجزاء التي تنتقل من أي نقطة على القطع الزائد إلى كل بؤرة.
- الطول البؤري : هو طول القطعة المركبة بين البؤرتين.
- المحور الأكبر أو المحور الحقيقي: هو القطعة التي تنتقل من النقطة أ إلى النقطة أ’، ويعادل طولها

- المحور الصغير أو المحور التخيلي: هو القطعة التي تنتقل من النقطة B إلى النقطة B’، طولها يعادل
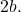
- الخطوط المقاربة : هي الخطوط المنقطة الموضحة على الرسم البياني. وسنرى أدناه كيفية حسابها.
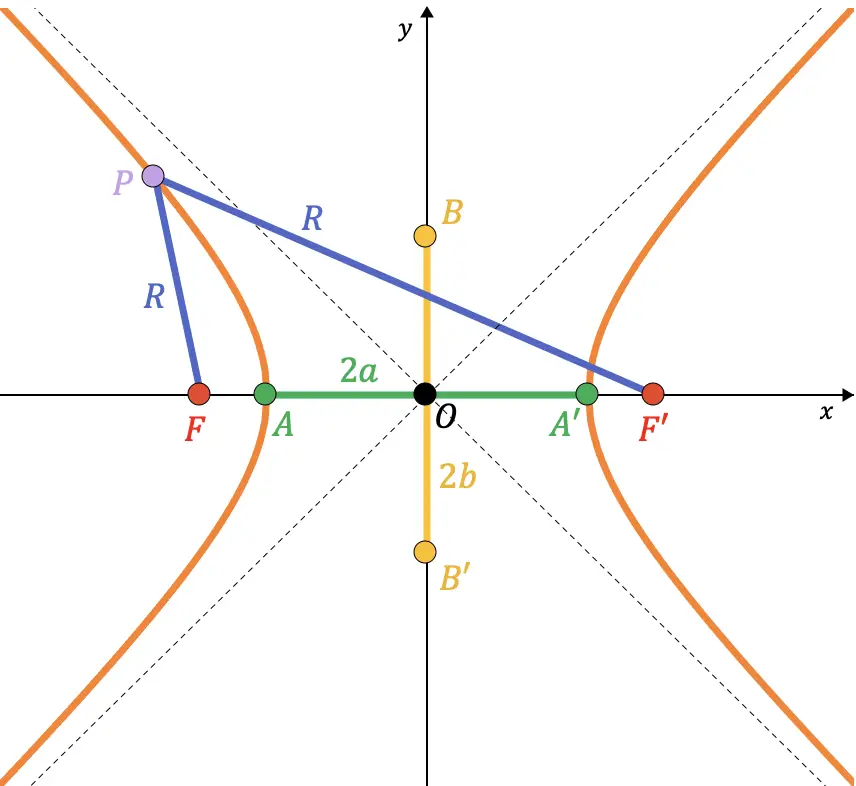
العلاقة بين عناصر القطع الزائد
أولًا، نقول إن نصف المحور يعني نصف المحور. على سبيل المثال، نصف المحور الحقيقي هو القطعة التي تنتقل من النقطة A إلى مركز القطع الزائد، وطولها هو
![]()
وبالتالي، هناك علاقة مهمة جدًا بين نصف المحور الحقيقي ونصف المحور التخيلي ونصف البعد البؤري. في الواقع، الصيغة التي سنستنتجها بعد ذلك تستخدم كثيرا في حل تمارين ومسائل القطع الزائد.
يجب أن تعلم أن النقطتين B وB’ للقطع الزائد تتوافق مع نقاط تقاطع المحور الرئيسي مع دائرة نصف القطر التخيلية
![]()
(المسافة شبه البؤرية) من المركز إلى النقطة A. لذلك، كما ترون في التمثيل البياني التالي، فإن القطعة التي تربط النقطة A والنقطة B تتزامن مع نصف قطر الدائرة المذكورة (
![]()
):
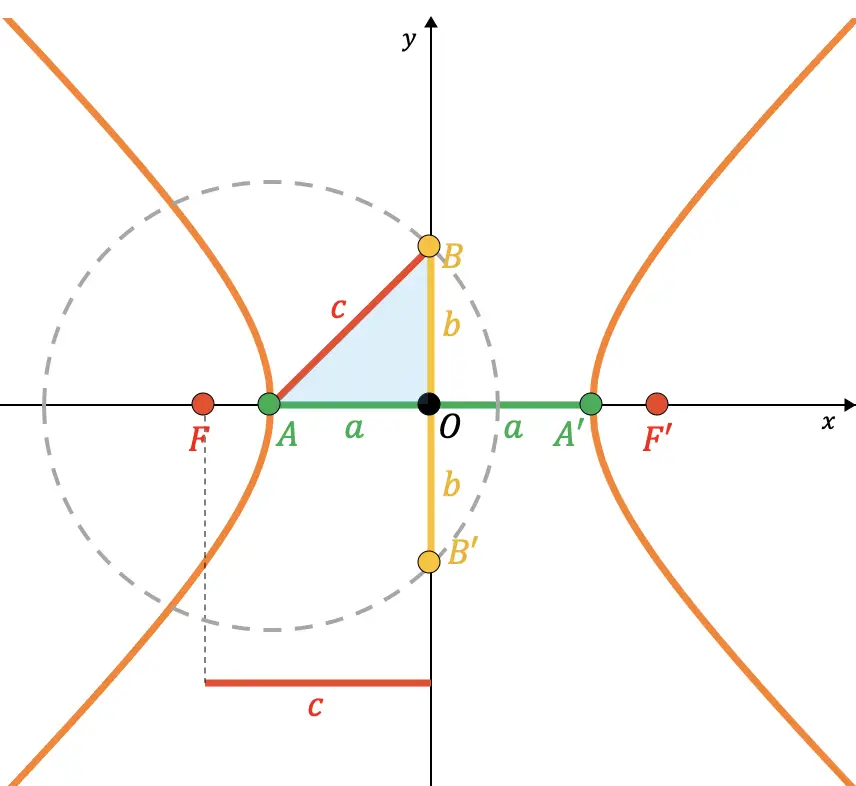
لذلك يمكن إثبات من نظرية فيثاغورس أن العلاقة بين المعلمات
![]()
و
![]()
هو ما يلي:
![]()
معادلة القطع الزائد
هناك عدة أنواع من معادلات القطع الزائد، حيث يتم استخدام واحدة أو أخرى للتعبير عنها رياضيًا، اعتمادًا على خصائصها. وبعد ذلك، سوف نقوم بتحليل كل منها بالتفصيل.
أولًا، لدينا المعادلة العادية للقطع الزائد. ثانيًا، سنرى صيغة مختلفة للمعادلة العادية، وهي المعادلة المختصرة أو القانونية للقطع الزائد. بعد ذلك، سوف ندرس كيف تكون المعادلة العامة للقطع الزائد. وأخيرًا، سنقوم بتحليل معادلات حالتين خاصتين من القطع الزائد: القطع الزائد متساوي الأضلاع والقطع الزائد المترافق .
المعادلة العادية للقطع الزائد
عندما نريد أن نحدد بمعادلة زائدة ذات مركز خارجي عند أصل الإحداثيات (النقطة (0,0))، يجب علينا استخدام الصيغة التالية:
صيغة المعادلة العادية للقطع الزائد في الإحداثيات الديكارتية هي كما يلي:
![]()
ذهب:
-

و

هي إحداثيات مركز القطع الزائد:
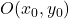
-

هو طول المحور شبه الرئيسي للقطع الزائد.
-

هو طول المحور شبه الأصغر للقطع الزائد.
باستخدام هذه المعادلة، يمكنك وصف القطع الزائدة التي يكون محورها البؤري أفقيًا (فروع مفتوحة إلى اليسار واليمين)، وهو ما تكون عليه القطوع الزائدة عادةً. لكن إذا عملنا مع محور بؤري رأسي (فروع مفتوحة من الأعلى إلى الأسفل)، فإن الإشارة السالبة تمر من المتغير y إلى المتغير x :
![]()
ذهب
![]()
و
![]()
هي، كما كان من قبل، إحداثيات مركز القطع الزائد والمصطلحات
![]()
و
![]()
لا يزالان هما المحور شبه الرئيسي والمحور شبه الأصغر للقطع الزائد، على الرغم من أنه، على عكس السابق، سيتم الآن توجيه هذين المحورين رأسيًا وأفقيًا على التوالي.
المعادلة الأساسية أو المخفضة للقطع الزائد
هذا النوع من معادلات القطع الزائد يشبه إلى حد كبير المعادلة العادية، والفرق الوحيد هو أن المعادلة القانونية تستخدم للتعبير التحليلي عن القطع الزائدة التي مركزها النقطة (0،0). لذلك، نستخدم المعادلة الأساسية أو المخفضة للقطع الزائد عندما يكون مركز القطع الزائد هو أصل الإحداثيات.
سوف نستنتج الآن صيغة المعادلة المخفضة للقطع الزائد من معادلته العادية:
![]()
إذا كان مركز القطع الزائد هو أصل الإحداثيات، أي النقطة (0,0)، فسيكون ما يلي صحيحًا دائمًا:
![]()
![]()
وبالتالي، فإن صيغة المعادلة الأساسية أو المخفضة للقطع الزائد ستكون:
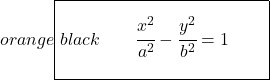
كما كان من قبل، إذا كان المحور البؤري عموديًا وليس أفقيًا، فسيكون المتغير السلبي x :
![]()
المعادلة العامة للقطع الزائد
صيغة المعادلة العامة للقطع الزائد هي كما يلي:
![]()
ومع ذلك، لكي تكون المعادلة أعلاه زائدة، فإن المعاملات
![]()
و
![]()
يجب أن تكون مختلفة عن الصفر، وفي نفس الوقت، لها علامة معاكسة.
معادلة القطع الزائد متساوية الأضلاع
القطع الزائد متساوي الأضلاع هو القطع الزائد الذي يكون فيه طول نصف المحور الحقيقي مكافئًا لطول نصف المحور الوهمي، وهذا يعني أن
![]()
ولذلك، فإن معادلة القطع الزائد متساوي الأضلاع هي:
![]()
بالإضافة إلى ذلك، الخطوط المقاربة للقطع الزائدة متساوية الأضلاع تكون متعامدة مع بعضها البعض. ومعادلات هذه الخطوط هي كما يلي:
![]()
![]()
إذا نظرنا بعناية، فإن هاتين المعادلتين هما منصفات الربع الأول (والثالث) والربع الثاني (والرابع)، على التوالي. لذا، إذا قمنا بتدوير القطع الزائد متساوي الأضلاع بمقدار 45 درجة إلى اليسار، فإن خطوط التقارب الخاصة به تحتل مكان محاور الإحداثيات:
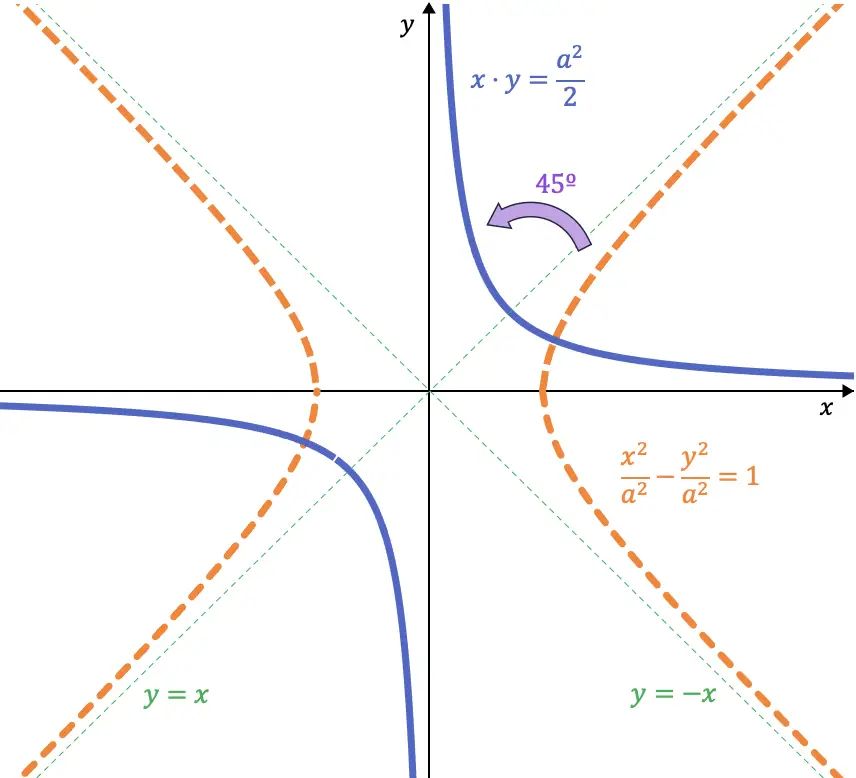
لذا، عندما ندور بزاوية 45 درجة، فإن معادلة القطع الزائد هي:
![]()
القطع الزائدة المترافقة
يتم اقتران القطع الزائد إذا كان المحور الحقيقي لأحدهما مساويا للمحور التخيلي للآخر . ولذلك، فإن الفرق الوحيد بين معادلات القطع الزائد المترافق هو المتغير الذي تم إبطاله، لأن معاملات المقامات يجب أن تظل كما هي.
فيما يلي مثال على معادلات قطعتين زائدتين مترافقتين مع بعضهما البعض:
![]()
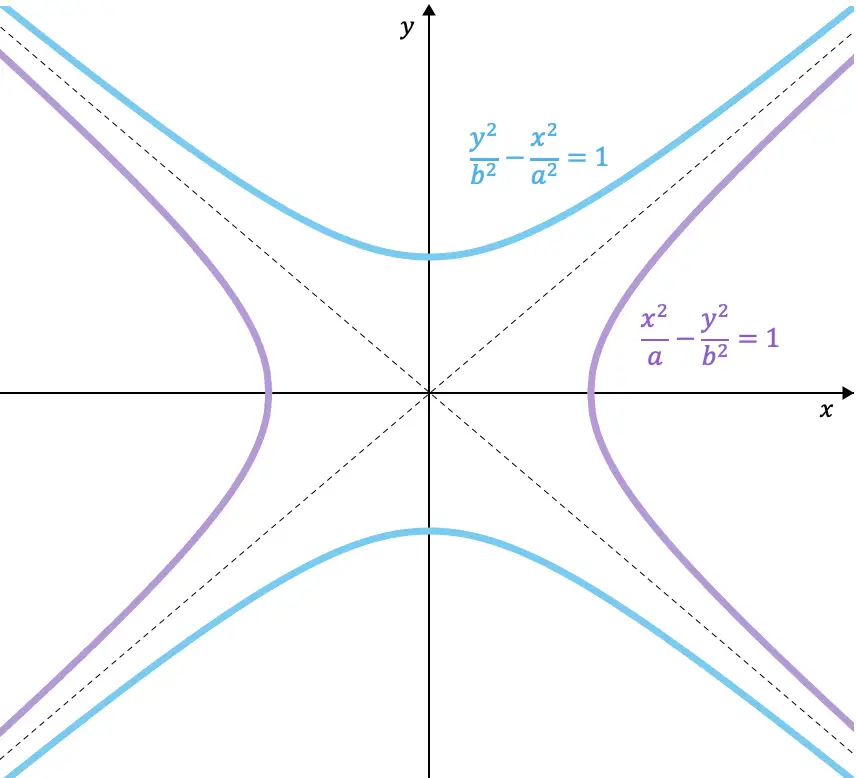
بالإضافة إلى ذلك، وكما ترون من القطوع الزائدة التي تم رسمها بيانيًا، فإن القطوع الزائدة المترافقة تشترك في نفس الخطوط المقاربة.
الخطوط المقاربة للقطع الزائد
كما رأيت في الرسوم البيانية السابقة، فإن كل قطع زائد له خطان مقاربان. تذكر أن الخط المقارب هو خط مستقيم يقترب جدًا من الدالة ولكنه لا يتقاطع معها أو يلامسها أبدًا.
لذا، فإن الصيغ التي تتوافق مع الخطوط المقاربة للقطع الزائد هي:
![]()
![]()
بحيث يمكن تحديد الخطوط المقاربة لأي قطع زائد بسهولة باستخدام معاملاتها
![]()
و
![]()
وهما على التوالي أطوال نصف المحور الحقيقي ونصف المحور التخيلي للقطع الزائد.
الانحراف في القطع الزائد
إن الانحراف المركزي للقطع الزائد هو معلمة مميزة تحدد مدى انفتاحه أو إغلاقه. عدديًا، يتم حساب الانحراف المركزي للقطع الزائد عن طريق قسمة طوله النصف البؤري على نصف محوره الحقيقي:
![]()
إن الانحراف المركزي لأي قطع زائد يكون دائمًا أكبر من 1:
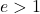 قيمة هذه المعلمة ذات صلة تمامًا، لأنها تشير إلى شكل القطع الزائد المحدد. كلما اقترب الانحراف المركزي للقطع الزائد من 1، كلما كانت فروعه أكثر انغلاقًا؛ ومن ناحية أخرى، كلما زادت قيمة الانحراف، كلما كانت فروعه مفتوحة.
قيمة هذه المعلمة ذات صلة تمامًا، لأنها تشير إلى شكل القطع الزائد المحدد. كلما اقترب الانحراف المركزي للقطع الزائد من 1، كلما كانت فروعه أكثر انغلاقًا؛ ومن ناحية أخرى، كلما زادت قيمة الانحراف، كلما كانت فروعه مفتوحة.
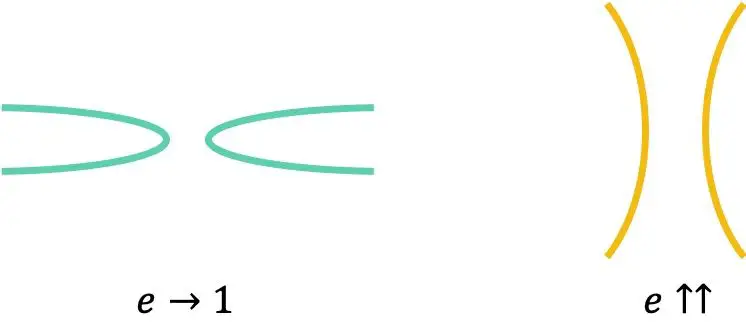
أخيرًا، تجدر الإشارة إلى أن الانحراف المركزي للقطع الزائد متساوي الأضلاع يساوي دائمًا
![]()
تم حل مشاكل القطع الزائد
يمكنك أدناه ممارسة المفاهيم التي رأيناها فيما يتعلق بالمسائل والتمارين التي تم حلها للقطع الزائد ومعادلة القطع الزائد.
التمرين 1
ما هي معادلة القطع الزائد الذي مركزه عند النقطة (-1.3)، وطول نصف المحور الحقيقي 3 وحدات، وطول نصف المحور التخيلي (الموازي للمحور Y) 7 وحدات؟
للعثور على معادلة القطع الزائد، ما عليك سوى تطبيق صيغة المعادلة العادية للقطع الزائد:
![]()
نعوض بإحداثيات مركز القطع الزائد في المعادلة:
![]()
![]()
وأخيرًا، نعوض بقيم المجهول
![]()
و
![]()
![]()
![]()
تمرين 2
أوجد إحداثيات المركز، والرءوس، والبؤر، وقيمة الانحراف المركزي وخطوط التقارب للقطع الزائد الذي يتم تعريف معادلته بواسطة:
![]()
بداية، تجدر الإشارة إلى أن المتغير السالب في المعادلة هو المتغير y ، وبالتالي فإن فروع القطع الزائد ستفتح على اليمين واليسار (المحور البؤري الموازي للمحور X).
ثانيًا، المعادلة تتوافق مع المعادلة الأساسية (أو المخفضة) للقطع الزائد، لذا فإن مركزها هو أصل الإحداثيات.
![]()
بمجرد أن نعرف مركز القطع الزائد، لحساب كل شيء آخر نحتاج إلى إيجاد قيمة نصف المحور الحقيقي (المعلمة
![]()
) ونصف المحور التخيلي (المعلمة
![]()
). يمكننا استنتاج كليهما من صيغة المعادلة الأساسية (أو المخفضة) للقطع الزائد:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
فإذا كانت هناك مسافة 5 وحدات بين المركز والرءوس، فهذا يعني أن رؤوس القطع الزائد هي:
![]()
لتحديد إحداثيات كل نقطة بؤرية، يجب معرفة قيمة نصف البعد البؤري (المعلمة
![]()
). ولهذا يمكننا استخدام الصيغة التي تربط عناصر القطع الزائد:
![]()
![]()
![]()
وبالتالي هناك مساحة 13 وحدة بين المركز والمنازل. وبالتالي فإن إحداثيات كل أسرة هي:
![]()
بعد ذلك، لحساب الانحراف المركزي للقطع الزائد، نحتاج إلى استخدام الصيغة المقابلة له:
![]()
وأخيرًا، نجد الخطوط المقاربة للقطع الزائد مع صيغها:
![]()
![]()
التمرين 3
احسب معادلة القطع الزائد الذي مركزه عند أصل الإحداثيات، مع العلم أن فرق المسافات من نقطة القطع الزائد إلى البؤرتين F(-4.0) وF(4.0) هو 6 وحدات.
أولاً، نظرًا لأن القطع الزائد له مركز عند أصل الإحداثيات، فسوف نستخدم المعادلة الأساسية أو المخفضة:
![]()
ثم، وفقًا لتعريف القطع الزائد، فإن القيمة المطلقة لفرق المسافات من إحدى نقاطه إلى البؤر (والتي هي في هذه الحالة 6) يجب أن تكون مساوية لطول المحور الحقيقي (
![]()
). حتى الآن:
![]()
![]()
![]()
![]()
ومن ناحية أخرى، فإن مركز القطع الزائد هو النقطة (0,0) والبؤرة هي النقطة (4,0). بحيث تكون المسافة إلى النقطتين (المعلمة
![]()
) هي 4 وحدات.
![]()
يمكننا الآن معرفة قيمة المعلمة
![]()
مع العلاقة الرياضية بين المعاملات المميزة الثلاثة للقطع الزائد:
![]()
![]()
![]()
![]()
إذن معادلة القطع الزائد هي:
![]()
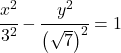
![]()