الخطوط المتعامدة (المتعامدة) -

ستجد في هذه الصفحة كل شيء عن الخطوط المتعامدة: ما هي، عندما يكون خطان متعامدين، كيفية حساب خط عمودي على آخر، خصائصه،… بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة وستكون قادرًا على تدرب مع التمارين التي تم حلها خطوة بخطوة.

ما هما الخطان المتعامدان؟

في الرياضيات، يكون الخطان متعامدين عندما يتقاطعان عند نقطة مكونة أربع زوايا قائمة متساوية (90 درجة).

بالإضافة إلى ذلك، يجب أن تكون متجهات الاتجاه لخطين متعامدين متعامدين أيضًا.

يُشار عمومًا إلى عمودي الخطين بالرمز

$\perp .$

من ناحية أخرى، تذكر أنه يوجد في المستوى 4 احتمالات في مفهوم الموضع النسبي بين خطين: يمكن أن يكون الخطان قاطعين أو متعامدين أو متطابقين أو متوازيين. إذا أردت، يمكنك التحقق من معنى كل نوع سطر على موقعنا.

كيف يمكنك معرفة ما إذا كان الخطان متعامدين؟

هناك طريقتان لتحديد متى يكون الخطان متعامدين، من خلال متجهات اتجاههما أو من خلال ميليهما . أدناه لديك شرح لكلا الطريقتين، رغم أنهما يخدمان نفس الغرض، إلا أننا ننصحك بمعرفة كيفية القيام بكلا الإجراءين لأن كل منهما يعتمد على كيفية التعبير عن الخطوط.

من متجهات الاتجاه للخطوط

إحدى الطرق لمعرفة متى يكون الخطان متعامدين هي استخدام متجهات الاتجاه للخطين المعنيين. تذكر أن متجه الاتجاه هو ذلك المتجه الذي يشير إلى اتجاه الخط.

إن متجهات الاتجاه لخطين متعامدين تكون أيضًا متعامدة بشكل متبادل. لذلك، إذا كان المنتج النقطي لمتجهات الاتجاه لخطين يساوي 0، فهذا يعني أن الخطوط متعامدة.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s =0 \quad \longrightarrow \quad r \perp s$

دعونا نرى كيف يتم تحديد عمودي خطين باستخدام مثال:

$\displaystyle r: \ \begin{cases} x=3-2t \\[2ex] y=6+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=4+3t \\[2ex] y=-2+2t \end{cases}$

يتم التعبير عن كلا الخطين كمعادلات حدودية، وبالتالي فإن مكونات متجه الاتجاه لكل خط هي الأرقام الموجودة أمام المعلمة

$t:$

$\vv{\text{v}}_r =(-2,3) \qquad \qquad \vv{\text{v}}_s=(3,2)$

بمجرد أن نعرف متجه الاتجاه لكل خط، نتحقق مما إذا كان الخطان متعامدين عن طريق حساب حاصل الضرب بين المتجهات:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-2,3)\cdot (3,2) = -2\cdot 3 +3\cdot 2= \bm{0}$

حاصل الضرب النقطي للمتجهين هو صفر، لذا فإن الخطوط المتعامدة.

منحدرات الخط

هناك طريقة أخرى لتحديد ما إذا كان الخطان متعامدين، وهي استخدام ميليهما. تذكر أن ميل الخط هو المعامل

$m$

للمعادلة الصريحة ومعادلة نقطة الميل للخط.

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

ويمكن أيضًا الحصول على ميل الخط من المعاملات

$A$

$B$

للمعادلة الضمنية (أو العامة) للخط:

$Ax+By+C= 0 \ \longrightarrow \ m = -\cfrac{A}{B}$

وبالتالي، فإن ميلي الخطين المتعامدين يكونان معكوسين وذوي إشارة متعاكستين، أي أن المساواة التالية تتحقق دائمًا:

$r \perp s \quad \longrightarrow \quad m_r=-\cfrac{1}{m_s}$

فإذا كان حاصل ضرب ميلي خطين مختلفين يساوي -1، فهذا يعني أن الخطين متعامدان:

$m_r\cdot m_s=-1\quad \longrightarrow \quad r \perp s$

على سبيل المثال، الخطان التاليان متعامدان:

$r: \ y=2x+4 \qquad \qquad s: \ y=-\cfrac{1}{2} \ x-5$

يمكننا أن نبين أنهما خطان متعامدان من ميليهما. ميل كل سطر هو :

$m_r = 2 \quad \quad m_s=-\cfrac{1}{2}$

الآن نضرب المنحدرات:

$\displaystyle 2 \cdot \left(-\frac{1}{2} \right) = -\cfrac{2}{2} = \bm{-1}$

الناتج بين المنحدرين يعادل -1، وهو ما يعني في الواقع وجود خطين متعامدين مع بعضهما البعض.

كيفية حساب خط عمودي على آخر؟

على الرغم من أنه قد يبدو من الصعب القيام بذلك، إلا أن العثور على خط عمودي على خط آخر أمر بسيط للغاية، ولهذا تحتاج فقط إلى متجه اتجاه عمودي على الخط ونقطة تنتمي إلى الخط.

الصعوبة الوحيدة هي أن الإجراء، كما كان من قبل، يعتمد على نوع المعادلة التي يتم التعبير عن الخطوط فيها. لأنه يمكن حساب خط عمودي على آخر من متجهات الاتجاه أو من المنحدرات .

من متجه الاتجاه لليمين

يمكن إيجاد خط عمودي على خط معطى آخر باستخدام متجه الاتجاه الخاص به. دعونا نرى كيف يتم ذلك مع مثال:

احسب الخط العمودي على الخط
$r$

ما يمر عبر هذه النقطة

$P(5,-1)$

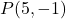
. ليكون مستقيما

$r:$

$\displaystyle r : \ 3x+2y-1=0$

أول ما علينا فعله هو تحديد متجه اتجاه الخط. في هذه الحالة، يتم تعريف الخط في شكل معادلة عامة (أو ضمنية)، وبالتالي يمكن الحصول على الإحداثيات الديكارتية لمتجه اتجاه الخط باستخدام المعاملين A و B للخط:

$\vv{\text{v}}_r =(-B,A)=(-2,3)$

وبمجرد أن نعرف متجه اتجاه الخط، علينا حساب المتجه العمودي عليه. للقيام بذلك، ما عليك سوى إدراج إحداثيات المتجه وتغيير إشارة أحدها (التي تريدها):

$\vv{\text{v}}_\perp =(3,2)$

إذن، نحن نعرف الآن اتجاه متجه الخط. وبالتالي فإن المعادلة الضمنية للخط ستكون كما يلي:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=-3 \end{array}$

$Ax+By+C \ \longrightarrow \ 2x-3y+C=0$

لذلك، يكفي تحديد المعلمة C. للقيام بذلك، نستبدل النقطة التي تنتمي إلى الخط المستقيم في معادلتها ونحل المعادلة الناتجة:

$P(5,-1)$

$2x-3y+C=0 \ \xrightarrow{x=5 \ ; \ y=-1} \ 2\cdot 5-3\cdot (-1)+C=0$

$10+3+C=0$

$13+C=0$

$C=-13$

وفي الختام فإن معادلة الخط العمودي هي:

$\bm{2x-3y-13=0}$

من منحدر الخط

هناك طريقة أخرى للعثور على خط عمودي على خط معين وهي من ميله. دعونا نرى كيف يتم حل هذا النوع من المشاكل من خلال مثال:

احسب الخط العمودي على الخط
$r$

ما يمر عبر هذه النقطة

$P(0,1)$

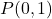
. ليكون مستقيما

$r:$

$\displaystyle r : \ y=4x-3$

منحدر الخط

$r$

شرق:

$m_r = 4$

بمجرد أن نعرف ميل الخط المستقيم، علينا إيجاد ميل الخط العمودي عليه. كما رأينا في الأقسام أعلاه، فإن ميلي الخطين المتعامدين يكونان معكوسين وتتغير إشارتهما. لذلك، لتحديد ميل الخط المتعامد، نحتاج إلى عكس الميل الموجود وتغيير إشارته:

$m_\perp =-\cfrac{1}{4}$

وبالتالي فإن المعادلة الصريحة للخط المتعامد ستكون كما يلي:

$y= mx+n$

$y=-\cfrac{1}{4} \ x + n$

وأخيرًا، نحسب الإحداثيات عند أصل الخط المتعامد عن طريق التعويض بإحداثيات النقطة في معادلة الخط:

$P(0,1)$

$y=-\cfrac{1}{4} \ x + n \ \xrightarrow{x=0 \ ; \ y=1} \ 1 =-\cfrac{1}{4}\cdot 0 + n$

$1 = n$

وباختصار فإن معادلة الخط العمودي هي:

$\bm{y=-}\mathbf{\cfrac{1}{4}} \ \bm{x + 1}$

خصائص الخطوط المتعامدة

جميع الخطوط المتعامدة لها الخصائص التالية:

العلاقة التناظرية : إذا كان مستقيم عمودي على خط آخر، فإن هذا الخط يكون عموديًا على السطر الأول أيضًا.

$r \bm{\perp} s \ \longrightarrow \ s \bm{\perp} r$

الخاصية غير الانعكاسية : من الواضح أنه لا يمكن لأي مستقيم أن يكون متعامدا مع نفسه.

$r \ \cancel{\bm{\perp}}} \ r$

النظرية: في الهندسة الإقليدية (في R2)، أي زوج من الخطوط المتعامدة مع خط ثالث يجب بالضرورة أن يكون متوازيًا. أي أنه إذا كان مستقيم عمودي على مستقيم آخر وهذا الخط عمودي أيضًا على خط ثالث، فإن الخطين الأول والأخير متوازيان.

حل مسائل الخطوط المتعامدة

التمرين 1

أي الخطوط التالية عمودي على الخط

$r: y=3x+4$

$a : \ y=3x-\cfrac{1}{3}$

$b : \ y=-\cfrac{1}{3} \ x+5$

$c : \ y=-4x-3$

$d : \ y=\cfrac{1}{3} \ x-5$

$e : \ y=-\cfrac{1}{3} \ x-2$

انظر الحل

منحدر الخط

$r$

هو 3:

$m_r=3$

وميلا الخطين المتعامدين معكوسان ومتعاكسان بإشارة، وبالتالي ميل أي خط عمودي على الخط

$r$

لا بد وأن:

$m_\perp=-\cfrac{1}{3}$

بحيث تكون الخطوط عمودية على الخط

$r$

هم الذين يساوي ميلهم

$-\cfrac{1}{3}$

. وهذا يعني الخطوط

$\bm{b}$

$\bm{e}.$

تمرين 2

حدد ما إذا كان الخطان التاليان متعامدين:

$\displaystyle r: \ \begin{cases} x=4-t \\[2ex] y=1-3t \end{cases}\qquad \qquad s: \ \cfrac{x-2}{4} = \cfrac{y+3}{6}$

انظر الحل

الحق

$r$

يتم التعبير عنها في شكل معادلة بارامترية، بحيث تكون مكونات متجه الاتجاه للخط المذكور هي الأرقام الموجودة أمام المعلمة

$t:$

$\vv{\text{v}}_r =(-1,-3)$

ومن ناحية أخرى، خط مستقيم

$s$

يتم تعريفه في شكل معادلة مستمرة، وبالتالي فإن إحداثيات متجه اتجاهه هي أرقام المقامات:

$\vv{\text{v}}_s =(4,6)$

بمجرد أن نعرف متجه الاتجاه لكل خط، يمكننا التحقق مما إذا كان الخطان متعامدين عن طريق حساب حاصل ضرب المتجهين:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-1,-3)\cdot (4,6) = -1\cdot 4 + (-3)\cdot 6= -22 \bm{\neq 0}$

حاصل الضرب النقطي للمتجهين غير صفر، لذا فإن الخطوط ليست متعامدة .

التمرين 3

أوجد الخط العمودي على الخط

$r$

ما يمر عبر هذه النقطة

$P(-2,1)$

. ليكون مستقيما

$r:$

$\displaystyle r : \ 4x-y+5=0$

انظر الحل

أول ما علينا فعله هو تحديد متجه اتجاه الخط. في هذه الحالة، يتم تعريف الخط على شكل معادلة عامة (أو ضمنية)، فيكون متجه اتجاهه هو:

$\vv{\text{v}}_r =(-B,A)=(1,4)$

بمجرد أن نعرف متجه الاتجاه للخط، علينا حساب المتجه العمودي عليه. للقيام بذلك، ما عليك سوى إدراج إحداثيات المتجه وتغيير إشارة أحدها (التي تريدها):

$\vv{\text{v}}_\perp =(4,-1)$

وبالتالي فإن المعادلة الضمنية للخط ستكون كما يلي:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (4,-1) \end{array} \right\}\longrightarrow \begin{array}{l}A=-1 \\[2ex] B=-4 \end{array}$

$Ax+By+C \ \longrightarrow \ -x-4y+C=0$

لذلك يكفي تحديد المجهول C. وللقيام بذلك، نعوض بالنقطة التي يمر عبرها الخط في معادلته:

$P(-2,1)$

$-x-4y+C=0 \ \xrightarrow{x=-2 \ ; \ y=1} \ -(-2)-4\cdot 1+C=0$

$2-4+C=0$

$-2+C=0$

$C=2$

وأخيرًا، معادلة الخط العمودي هي:

$\bm{-x-4y+2=0}$

التمرين 4

أوجد معادلة نقطة الميل للخط العمودي على الخط

$r$

ما يمر عبر هذه النقطة

$P(3,-2)$

. ليكون مستقيما

$r:$

$\displaystyle r : \ y=5x+1$

انظر الحل

منحدر الخط

$r$

شرق:

$m_r = 5$

بمجرد أن نعرف ميل الخط المستقيم، علينا إيجاد ميل الخط العمودي عليه. للقيام بذلك، ما عليك سوى عكس الميل الموجود وتغيير علامته:

$m_\perp =-\cfrac{1}{5}$

أخيرًا، ما عليك سوى التعويض بالميل الموجود وإحداثيات النقطة في معادلة نقطة الميل للخط:

$y -y_0=m(x-x_0)$

$y-(-2)=-\cfrac{1}{5} (x- 3)$

$\bm{y+2=}\mathbf{-\cfrac{1}{5}}\bm{ (x- 3)}$

التمرين 5

الحق

$r$

يمر بالنقطتين (2،1) و (4،2) والخط

$s$

يمر بالنقطتين (-1,2) و (1,-2). تحديد ما إذا كان هذان خطان متعامدان أم لا.

انظر الحل

للتحقق مما إذا كان هذان الخطان متعامدين، سنحسب ميليهما ثم نرى ما إذا كانا يحترمان العلاقة العمودية. تذكر أن صيغة ميل الخط هي:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

منحدر الخط

$r$

شرق:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{2-1}{4-2} = \cfrac{1}{2}$

منحدر الخط

$s$

شرق:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{-2-2}{1-(-1)} = \cfrac{-4}{2}=-2$

للتحقق من عمودي الخطين، يجب علينا معرفة ما إذا كان ميل أحد الخطين هو معكوس الميل الآخر. في هذه الحالة، يكون الميلان معكوسين ولهما أيضًا إشارات متضادة، وبالتالي يكون الخطان متعامدين مع بعضهما البعض.