تطابق وظيفي

يوليو 4, 2023

هنا سوف تجد ما هي وظيفة الهوية. بالإضافة إلى ذلك، سوف تكون قادرًا على رؤية كيفية تمثيل وظيفة الهوية بيانيًا وما هي خصائصها.

ما هي وظيفة الهوية؟

دالة الهوية هي تلك الوظيفة التي لها نفس قيمة الوسيطة كصورة. يمكن التعبير عن وظيفة الهوية بالمصطلح id .

وبالتالي فإن التعبير الرياضي لدالة الهوية هو:

$f(x)=x$

على سبيل المثال، صورة دالة الهوية لـ x=1 تساوي 1، صورة x=2 تساوي 2، صورة x=3 تساوي 3،…

$\begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}$

دالة الهوية هي مثال على دالة خطية. في الرابط التالي يمكنك رؤية المزيد من الأمثلة على هذا النوع من الوظائف:

➤ انظر: أمثلة على الدوال الخطية

تمثيل رسومي لوظيفة الهوية

الرسم البياني لوظيفة الهوية يتوافق مع الخط الذي يمثل منصف الربعين الأول والثالث.

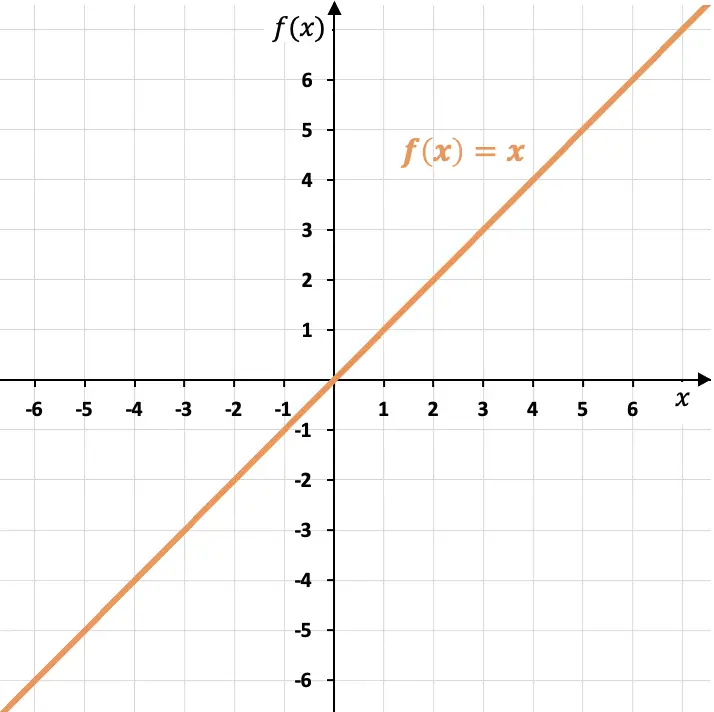
تطابق وظيفي

كما ترون، فإن دالة الهوية تمر عبر أصل الإحداثيات (النقطة (0,0)) ولها ميل يساوي الوحدة (م=1)، إذ تزداد وحدة واحدة من المتغير ولكل قيمة مستقلة المتغير X. بالإضافة إلى ذلك، تشكل دالة الهوية زاوية 45 درجة مع المحور X.

خصائص وظيفة الهوية

تتميز وظيفة الهوية بالخصائص التالية:

مجال دالة الهوية هو جميع الأعداد الحقيقية:

$\text{Dom } f=\mathbb{R}$

يتكون نطاق (أو مدى) دالة الهوية أيضًا من جميع الأعداد الحقيقية:

$\text{Im } f=\mathbb{R}$

وظيفة الهوية هي وظيفة مستمرة وذاتية.

بالإضافة إلى ذلك، تتكون دالة الهوية من دالة فردية، مما يعني أنها دالة متماثلة بالنسبة إلى أصل الإحداثيات.

$\displaystyle f(-x)=-f(x)$

➤ انظر: دالة متماثلة غريبة

دالة الهوية تتزايد على مجالها بأكمله، وميلها يساوي 1.

$m=1$

يتقاطع المحور x (محور OX) والمحور y (المحور Y) في نفس النقطة: أصل الإحداثيات.

$(0,0)$

يمكن تصنيفها على أنها دالة متعددة الحدود من الدرجة الأولى.

تعمل وظيفة الهوية كعنصر محايد في تكوين الوظيفة . بحيث أن أي دالة مكونة من دالة الهوية ينتج عنها الدالة نفسها.

$f\circ id =id \circ f=f$

القيمة
$x=0$

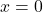
هو الجذر الوحيد لهذا النوع من الوظائف.

حد دالة الهوية عندما تتجه x نحو زائد ما لا نهاية أو ناقص ما لا نهاية يعطي على التوالي زائد ما لا نهاية وناقص ما لا نهاية:

$\displaystyle\lim_{x\to +\infty} f(x)=+\infty$

$\displaystyle\lim_{x\to -\infty} f(x)=-\infty$

وبالتالي فإن وظيفة الهوية ليس لها خط مقارب.

مشتق دالة الهوية هو الدالة الثابتة ذات القيمة 1:

$f(x)=x \ \longrightarrow \ f'(x)=1$

تكامل دالة الهوية هو الدالة التربيعية:

$\displaystyle \int x \ dx= \frac{x^2}{2} + C$

➤ انظر: صيغة الدالة التربيعية

اترك تعليقاً إلغاء الرد