مثلث تارتاليا (أو باسكال)

في هذه الصفحة نشرح ما هو مثلث تارتاليا، والذي يسمى أيضًا مثلث باسكال. سوف نتعلم كيفية بناء مثلث تارتاليا (أو باسكال) رياضيًا، بالإضافة إلى ما يستخدم وما هي جميع خصائصه. وأخيرًا، نوضح كيف ومتى ظهر هذا المثلث المهم جدًا.

ما هو مثلث تارتاليا (أو باسكال)؟

مثلث تارتاليا ، ويسمى أيضًا مثلث باسكال ، هو تمثيل رياضي للأعداد الصحيحة المرتبة على شكل مثلث. يتم استخدام مثلث تارتاليا (أو باسكال) لإجراء الحسابات الرياضية.

هذا هو تعريف مثلث تارتاليا أو باسكال، لكنك بالتأكيد تفهم المفهوم بشكل أفضل مع صورة المثلث:

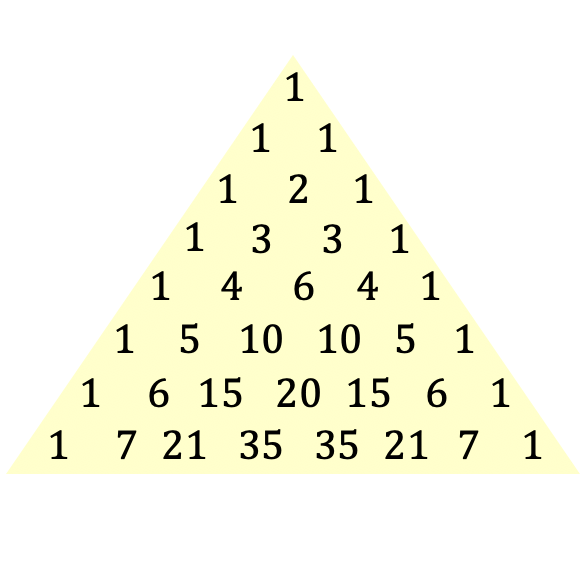
يُسمى مثلث تارتاليا أيضًا بمثلث باسكال نسبة إلى الفيلسوف وعالم الرياضيات الفرنسي بليز باسكال، الذي قدم هذا التعبير الثلاثي في عام 1654، على الرغم من أن هذا المثلث معروف بالفعل منذ العصور القديمة. أدناه، سوف نتعمق في تاريخ هذا المثلث بالتحديد.

كيف يتم بناء مثلث تارتاليا أو باسكال؟

كما رأيت في مثلث باسكال (أو تارتاليا)، هناك الكثير من الأرقام، لكن هذا لا يعني أنه يجب علينا حفظها عن ظهر قلب (الحمد لله). هناك صيغة تسمح لك بالعثور بسهولة على جميع الأرقام الموجودة في مثلث باسكال أو تارتاليا، ما عليك سوى حل مبالغ بسيطة.

لبناء مثلث تارتاليا أو باسكال، عليك أن تبدأ من أعلى المثلث، والذي يكون دائمًا 1، ثم يتم حساب الخطوط أدناه. كل رقم في السطر التالي هو مجموع الرقمين الموجودين فوقه مباشرة، ما عدا طرفي السطرين اللذين يكونان دائما 1.

لذلك، يمكنك حساب أي عدد تريده من خطوط مثلث Tartaglia، لأنه يمكنك إضافة خطوط تباعًا عن طريق إضافة الأرقام.

ما هو استخدام مثلث تارتاليا أو باسكال؟

إن معرفة كيفية بناء مثلث تارتاليا أمر جيد جدًا، ولكن… ما هو استخدام هذا المثلث الحسابي؟ حسنًا، مثلث تارتاليا (أو باسكال) له العديد من التطبيقات في الرياضيات، وخاصة في مجال الجبر.

أرقام اندماجية

بادئ ذي بدء، يتم استخدام مثلث تارتاليا لحساب الأعداد التوافقية مباشرة، وتسمى أيضًا المعاملات ذات الحدين. إذا كنت لا تعرف ما هي هذه الأنواع من العمليات، يمكنك البحث عنها في موقعنا (لدينا محرك بحث في أعلى اليمين) لأننا كتبنا مقالاً مفصلاً نشرح فيه كيفية حلها وأنت هناك أنت سوف تجد أيضًا أمثلة وتمارين تم حلها خطوة بخطوة. لكن باختصار، التعبير الجبري للعدد التوافقي هو كما يلي:

$\displaystyle \begin{pmatrix} n \\ k \end{pmatrix}$

حسنًا، يمكن تحديد جميع الأعداد التوافقية بسهولة باستخدام مثلث تارتاليا، لأن حل كل معامل ذو الحدين يعادل عددًا من هذا التعبير الثلاثي كما هو موضح في الشكل التالي:

الأعداد التوافقية لمثلث Tartaglia أو Pascal

على سبيل المثال، الرقم التوافقي

$\displaystyle \begin{pmatrix} 4 \\ 2 \end{pmatrix}$

ترجع 6، لأنه في مثلث Tartaglia يوجد 6 بدلاً من ذلك.

لذا، إذا كنت تعرف كيفية إنشاء مثلث تارتاليا أو باسكال، فيمكنك حساب أي رقم اندماجي بسرعة ودون استخدام صيغته.

نيوتن ذات الحدين

الاستخدام الآخر لمثلث تارتاليا (أو باسكال) هو أن تكون قادرًا على حساب قوى ذات الحدين (انقر على هذا الرابط لمعرفة ما هي ذات الحدين).

من الأمثلة على تقوية ذات الحدين الهويات البارزة، مثل:

$(a+b)^2$

تعتبر الهويات الرائعة مهمة جدًا للرياضيات، لأنها تتيح لنا حفظ العديد من العمليات الحسابية وحل العمليات المعقدة بشكل مباشر وسريع. ولهذا السبب نوصي بمراجعة الرابط التالي إذا كنت لا تزال لا تعرف ما هي الهويات البارزة .

كما رأيت في الرابط السابق، يمكن حل المنتجات البارزة مباشرة باستخدام صيغها. ولكن… ماذا يحدث عندما يتم رفع الزوج إلى المكعب أو إلى درجة أعلى؟

$\begin{array}{c} (a+b)^3 = \ ? \\[3ex] (a+b)^4 = \ ? \\[3ex] (a+b)^5 = \ ? \\[3ex] \bm{\vdots} \end{array}$

حسنًا، يمكن حساب هذه الحدين بطريقة بسيطة جدًا باستخدام مثلث تارتاجليا بفضل نظرية ذات الحدين (أو ذات الحدين لنيوتن). على الرغم من إتقان الطريقة، إلا أنها سريعة التطبيق، لكن لشرحها جيدًا تحتاج إلى صفحة كاملة. لذلك، إذا كنت مهتمًا أكثر بكيفية حل هذا النوع من ذات الحدين، فانقر على الصفحة المرتبطة ويمكنك رؤية كيفية حل ذلك.

التوافقيات

يمكن أيضًا استخدام مثلث تارتاليا، أو مثلث باسكال، لتحديد التركيبات والاحتمالات.

إذا واجهنا مشكلة حيث نحتاج إلى تحديد عدد المجموعات المختلفة التي يمكن تكوينها من مجموعة بغض النظر عن الترتيب، فيمكننا استخدام مثلث تارتاليا.

على سبيل المثال، إذا كان لدينا 5 بطاقات، لمعرفة عدد الطرق التي يمكننا من خلالها اختيار 3، ما عليك سوى الانتقال إلى العمود الثالث (العمود الأول هو صفر) من الصف الخامس (الصف الأول هو أيضًا الصف 0) من مثلث تارتاليا. الرقم الموجود في هذا الموضع (10) يتوافق مع عدد الاحتمالات المتاحة لاختيار 3 بطاقات.

$1 \quad 5 \quad 10 \quad \color{blue}\boxed{ \color{black}10} \color{black} \quad 5 \quad 1$

لذلك، من 5 بطاقات، يمكن تشكيل 10 مجموعات مختلفة من ثلاث بطاقات.

خصائص مثلث تارتاليا أو باسكال

يتميز مثلث تارتاليا، ويسمى أيضًا مثلث باسكال، بالخصائص التالية:

مثلث تارتاليا (أو باسكال) متماثل، أي أن الخط العمودي الذي يقسم المثلث بأكمله إلى مثلثين متساويين الأضلاع هو محور التناظر.

المجموع الأفقي لجميع الأرقام في أي خط من مثلث باسكال يساوي قوة 2.

أقطار مثلث تارتاليا مهمة أيضًا: الأرقام الموجودة على القطر الأول (القطر الخارجي) هي أرقام واحدة، والقطري الثاني يتكون من تسلسل جميع الأعداد الطبيعية، والقطري الثالث يتوافق مع الأعداد المثلثية، ويتكون القطر الرابع من الأعداد الرباعية (أو الرباعية السطوح).

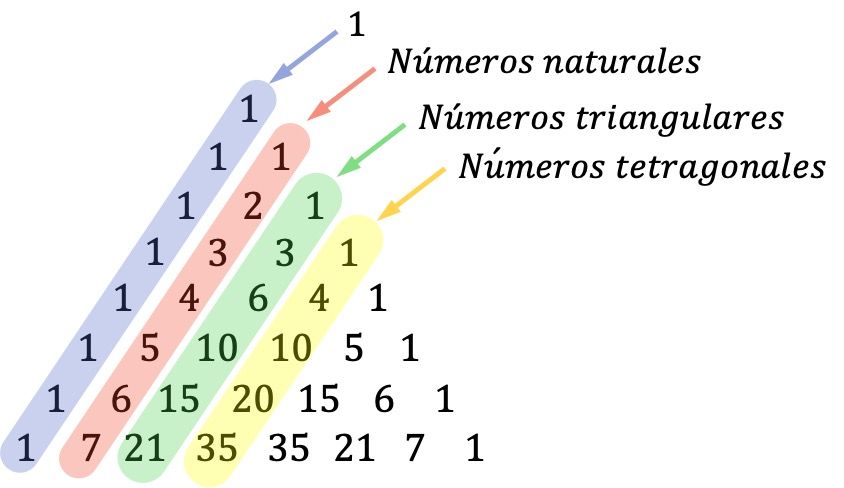
مثلث تارتاليا أو أرقام باسكال الثلاثية والرباعية

الأعداد المثلثية هي أرقام يمكن تمثيلها على شكل مثلث. والأعداد الرباعية هي تلك التي تشكل أهرامات مثلثية.

إذا كنت لا تعرف ما هي الأعداد المثلثية أو الرباعية، فلن يحدث شيء، إنه مجرد فضول حول مثلث تارتاليا. ومع ذلك، عليك أن تعرف معنى الأعداد الطبيعية (الأرقام المستخدمة لحساب العناصر).

باستثناء الرقم 1، إذا كان الرقم الأول في السطر هو رقم أولي، فإن جميع الأرقام الموجودة في نفس السطر قابلة للقسمة على هذا الرقم. على سبيل المثال، في الصف الثامن (1-7-21-35-35-21-7-1)، يمكن تقسيم الأرقام 7 و21 و35 على 7 (سبعة هو رقم أولي).

خصوصية أخرى لمثلث تارتاليا هي أنه يمكن العثور على سلسلة فيبوناتشي عن طريق إضافة الأقطار بطريقة معينة:

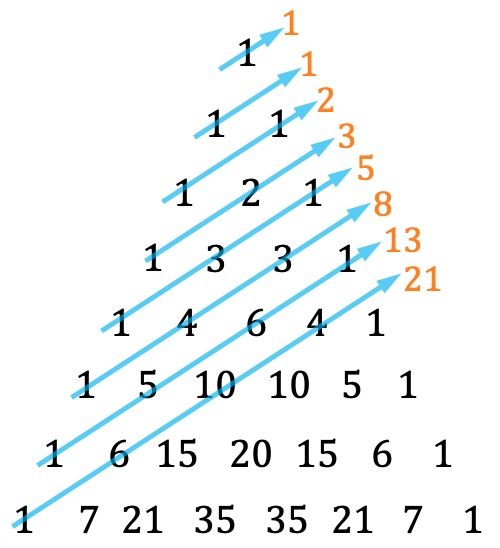
تذكر أن كل حد من متتابعة فيبوناتشي يساوي مجموع الحدين السابقين، الحدين الأولين هما 1 و1. وبالتالي فإن الأرقام التي تنتمي إلى متوالية فيبوناتشي هي: 1، 1، 2، 3، 5، 8 ، 13، 21، 34، 55، 89، 144، 233،…

فإذا أضفنا رقمين متتاليين من القطر الثالث لمثلث باسكال (1-3-6-10-15-…) نحصل على مربع كامل (1، 4، 9، 16، 25،…).

إذا رسمنا الأعداد الزوجية لمثلث باسكال بلون واحد والأعداد الفردية بلون آخر، نحصل على شكل مثلث سيربينسكي، وهي مجموعة هندسية مشهورة. أدناه يمكنك رؤية مثلث باسكال الذي يبلغ ارتفاعه 512 ممثلًا بالأرقام الفردية باللون الأسود والأرقام الزوجية باللون الأبيض:

مثلث سيربينسكي من تاتاليا أو مثلث باسكال

يقول حدسية Singmaster أن عدد المرات التي يحدث فيها كل رقم أكبر من 1 هو عدد محدود. أو بمعنى آخر، على الرغم من أن عدد الصفوف في مثلث تارتاليا لا نهائي، إلا أن عدد مرات ظهور كل رقم باستثناء 1 هو عدد محدود. ومن باب الفضول، فإن الرقم 3003 هو الرقم الوحيد المعروف حتى الآن أنه يظهر حتى ثماني مرات في المثلث.

تاريخ مثلث تارتاليا أو باسكال

الآن بعد أن عرفنا كيف يبدو مثلث تارتاليا، دعونا نرى متى تم اختراع هذا المثلث الرياضي المميز جدًا.

على الرغم من أن اسم المثلث الحسابي ينسب بشكل أساسي إلى العالمين المشهورين تارتاليا وباسكال، إلا أن هذا المثلث الجبري كان مستخدمًا بالفعل من قبل.

يعود أول سجل لمثلث يتكون من معاملات ذات الحدين إلى القرن العاشر في الهند. إلا أن الفرس بدأوا بدراسة خصائصه، وأبرزهم عالما الرياضيات الكراجي (953-1029) وعمر الخيام (1048-1131). ولهذا السبب تم الترويج له في إيران باسم مثلث الخيام باسكال أو حتى ببساطة مثلث الخيام .

بدأ تقديم هذا المثلث إلى الصين في القرن الحادي عشر على يد عالم الرياضيات جيا شيان، ولكن في وقت لاحق في القرن الثالث عشر قدمه يانغ هوي على أنه المثلث الحسابي . ولهذا السبب، في الدولة الآسيوية يسمونه مثلث يانغ هوي .

ووصل المثلث الرياضي إلى القارة الأوروبية لاحقاً عن طريق الألماني بيتروس أبيانوس، الذي نشر تحديداً عام 1527 في كتابه Rechnung . ومن هناك، قام عالم الجبر الإيطالي الشهير نيكولو فونتانا تارتاجليا بدراسة المثلث بعمق خلال النصف الأول من القرن السادس عشر، وتكريمًا له في دول مثل إيطاليا يُعرف باسم مثلث تارتاجليا.

وأخيرًا، أوضح الفرنسي بليز باسكال العديد من خصائص المثلث التي درسها في منشوره لرسالة حول المثلث الحسابي عام 1654، ومن هنا جاء اسم مثلث باسكال. تجدر الإشارة إلى أن بعض هذه الخصائص كانت معروفة بالفعل، لكن باسكال هو من قام بإظهارها عن طريق الاستقراء الرياضي.

مثلث تارتاجليا (أو مثلث باسكال).