ستجد هنا شرحًا لحل جميع أنواع الهويات البارزة (أو المنتجات البارزة). ستتمكن من رؤية صيغ جميع الهويات البارزة، بالإضافة إلى الأمثلة والتمارين التي تم حلها خطوة بخطوة. بالإضافة إلى ذلك، سنوضح لك فيما تستخدم هذه القواعد الرياضية الشهيرة.
👉👉 نشرح أدناه كل هوية بارزة خطوة بخطوة، ولكن إذا كنت تفضل ذلك، يمكنك الانتقال مباشرة إلى الجدول 😉 حيث يتم تلخيص جميع الصيغ . 👈👈
ما هي الهويات البارزة (أو المنتجات البارزة)؟
الهويات الرائعة ، وتسمى أيضًا المنتجات الرائعة أو المساواة الرائعة ، هي قواعد رياضية تسمح بحل العمليات ذات كثيرات الحدود مباشرة.
صيغ الهوية الأكثر شيوعًا هي مربع المجموع ، ومربع الفرق (أو الطرح)، والمجموع مضروبًا في الفرق .

ولكن أدناه لن نعلمك كيفية حساب هذه المنتجات البارزة فحسب، بل سنعرض لك أيضًا جميع أنواع الهويات البارزة الموجودة.
صيغ الهوية البارزة (أو المنتجات)
بمجرد أن رأينا تعريف المنتجات البارزة (أو المساواة البارزة)، سنرى ما هي صيغ الهويات البارزة. من ناحية أخرى، إذا كنت مهتمًا بالعروض التوضيحية للصيغة، فيمكنك عرض الصيغة الخاصة بها من خلال النقر على أزرار “عرض العرض التوضيحي”.
مربع من المبلغ
يعد مربع المبلغ ، أو مجموع المربع ، أحد الهويات الرئيسية البارزة. بتعبير أدق، إنها ذات الحدين ذات حدين موجبين للقوة 2، وهذا يعني أن تعبيرها الجبري هو (a+b) 2 .
لذا فإن صيغة مربع المجموع هي:

إذا بدأنا من ذات الحدين موجبة مرفوعة إلى 2:
![]()
رياضياً، المربع أعلاه يعادل العامل
![]()
مضروبا في نفسه:
![]()
لذلك، نحن نضرب كثيرات الحدود باستخدام خاصية التوزيع:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
ومن بين الشروط الأربعة التي تم الحصول عليها،
![]()
و
![]()
تبدو متشابهة حتى نتمكن من تجميعها:
![]()
لدرجة أننا وصلنا بالفعل إلى التعبير عن صيغة المجموع التربيعي، والتي اشتقت منها:
![]()
من باب الفضول، فإن تطوير التعبير لهذا النوع من المنتجات الرائعة يسمى ثلاثي الحدود المربع المثالي.
بحيث يكون مربع المجموع يساوي مربع الحد الأول، مضافًا إليه ضعف حاصل ضرب الأول في الثاني، بالإضافة إلى مربع الثاني.
لذا لحل مجموع تربيعي، لا يكفي رفع كل إضافة إلى كليهما، ولكن بالإضافة إلى ذلك، يجب ضرب الجمعين مع بعضهما البعض وفي 2. ومن المهم أن نتذكر ذلك لأن خطأ نموذجيًا جدًا من هذا النوع من المنتج ومن اللافت للنظر أن ننسى هذا المصطلح.

مثال:
- احسب الهوية البارزة التالية من خلال تطبيق الصيغة المقابلة لها:
![]()
كما رأينا للتو، فإن صيغة المساواة الملحوظة للمجموع المربع هي:
![]()
ولذلك، يجب علينا أولا تحديد المعلمات
![]()
و
![]()
من الصيغة. في هذه الحالة،
![]()
يمثل
![]()
من الزوج و
![]()
تتوافق مع رقم 5:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
والآن بعد أن عرفنا قيم
![]()
وبناءا على
![]()
يمكننا استخدام صيغة تربيع ذات الحدين الموجبين للعثور على النتيجة:

مربع الفرق
مربع الفرق ، أو تربيع الفرق ، هو أحد الهويات الثلاثة البارزة الأكثر استخدامًا. على وجه الخصوص، فهو يتوافق مع ذات الحدين المكونة من حد موجب وحد سالب آخر مرفوع إلى 2، وهذا يعني أن تعبيره الجبري هو (ab) 2 .
لذا، فإن صيغة مربع الفرق (أو مربع الطرح) هي كما يلي:

من التعبير ذي الحدين للطرح التربيعي:
![]()
من الواضح أن القوة السابقة تساوي منتج العامل
![]()
مضروبا في نفسه:
![]()
الآن نضرب القوسين بتطبيق خاصية التوزيع:
![Rendered by QuickLaTeX.com \begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b46073fd758d93fff8956f0a8dd57af_l3.png)
لذلك عليك فقط تجميع المصطلحات المتشابهة معًا لإنهاء التحقق من الصيغة:
![]()
ثم يتم إثبات صيغة مربع الفرق رياضيا:
![]()
بحيث يكون مربع الفرق يساوي مربع الحد الأول ناقص ضعف حاصل ضرب الأول في الثاني، بالإضافة إلى مربع الثاني.
أما بالنسبة للمساواة الملحوظة في مجموع التربيع فلا ننسى أن نضع الحد الأوسط للصيغة، فالمعادلة التالية غير صحيحة:

مثال:
- حل المساواة الملحوظة التالية للفرق التربيعي:
![]()
إنه المنتج البارز للطرح التربيعي، لذلك من الضروري تطبيق الصيغة المقابلة له:
![]()
بعد ذلك، يجب علينا تحديد ما هي قيم المجهولة.
![]()
و
![]()
من الصيغة. في هذه الحالة،
![]()
هو المتغير
![]()
و
![]()
تتوافق مع رقم 3:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1bb2d14a30d2cdabae6458f5df32392a_l3.png)
لاحظ أن الإشارة السالبة ليست جزءًا من المعلمة
![]()
ولكن يجب عليك دائمًا أخذ الرقم بدون الإشارة لتطبيق هذه الصيغة بشكل صحيح.
لذلك نحن نعرف بالفعل قيم
![]()
وبناءا على
![]()
لذلك يكفي استبدال هذه القيم في الصيغة لحل الهوية البارزة:

المجموع بالفارق
يعد حاصل ضرب المجموع والفرق أحد الهويات الثلاث الأكثر استخدامًا. كما يوحي اسمها، فهي ذات حدين موجبة مضروبة في ذات الحدين المترافقين (نفس ذات الحدين ولكن مع تغيير الإشارة الوسيطة)، وهذا يعني أن التعبير الجبري لهذا النوع من المنتجات الرائعة هو (a +b) · (ab) .
صيغة الهوية الرائعة لمنتج المبلغ بالفارق هي كما يلي:

البدء من حاصل ضرب المجموع بطرح أي حدين:
![]()
لتوضيح الصيغة، نحتاج ببساطة إلى ضرب القوس الأول في القوس الثاني باستخدام خاصية التوزيع:
![Rendered by QuickLaTeX.com \begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-346d3d7ca4da1e71fad52c84a33ef4fc_l3.png)
الآن نقوم بتجميع المصطلحات المتشابهة معًا:
![]()
وبذلك نكون قد حققنا التعبير عن المساواة الرائعة. وهكذا يتم توضيح صيغة هذا النوع الرائع من الهوية:
![]()
وبالتالي فإن حاصل ضرب المجموع في الفرق بين كميتين يساوي الفرق بين مربعي هاتين الكميتين. أو بمعنى آخر، فإن ضرب مجموع حدين مختلفين عن طريق طرح نفس الحدين يعادل تربيع كل حد من الحدين وطرحهما.
مثال:
- أوجد، باستخدام الصيغة المقابلة، المنتج البارز التالي للمجموع بفارق مصطلحين مختلفين:
![]()
كما رأينا أعلاه، فإن صيغة المساواة الملحوظة للمجموع مضروبًا في الفرق هي كما يلي:
![]()
أولًا، ما علينا فعله هو تحديد قيم الحروف
![]()
و
![]()
من الصيغة. في هذه الحالة
![]()
تتوافق مع المتغير
![]()
و
![]()
تتوافق مع رقم 2
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-87b76b09924467ba75f033336e6a18e5_l3.png)
وعندما نعرف بالفعل القيم التي تأخذها المعلمات
![]()
و
![]()
نطبق صيغة حاصل ضرب المجموع بالفرق:
مربع من ثلاثي الحدود
مربع ثلاثية الحدود (كثيرة الحدود مكونة من 3 حدود) يساوي مربع الحد الأول، زائد مربع الحد الثاني، زائد مربع الحد الثالث، زائد ضعف الأول على الثاني، زائد ضعف الأول بالثالث، بالإضافة إلى ضعف الثانية للثالث.

من أي ثلاثية الحدود:
![]()
يمكن تحليل المربع أعلاه إلى ثلاثية الحدود مضروبة في نفسها:
![]()
الآن نحل ضرب كثيرات الحدود:
![]()
وأخيرًا، نقوم بتجميع المصطلحات المتشابهة:
![]()
بهذه الطريقة، وصلنا بالفعل إلى تعبير الصيغة، لذلك تم توضيح صيغة مربع ثلاثي الحدود:
![]()
مثال:
- أوجد المساواة الملحوظة التالية:
![]()
صيغة مربع ثلاثي الحدود هي:
![]()
كما هو الحال في جميع المعادلات البارزة، يجب عليك أولاً تحديد قيم المجهولة في الصيغة. في هذا التمرين
![]()
شرق
![]()
المعامل
![]()
تتوافق مع
![]()
و
![]()
هو المصطلح المستقل 3:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55e06f44486e75e9153a60d36e83bc37_l3.png)
وعندما نعرف القيم بالفعل، ما عليك سوى استبدال هذه القيم في الصيغة وإجراء الحسابات:

الهويات (أو المنتجات) البارزة مكعبة
لقد قمنا للتو بدراسة جميع المتطابقات البارزة المربعة، أي جميع أنواع المتطابقات البارزة التي تتكون من قوى مرفوعة إلى 2. حسنًا، سنقوم الآن بتحليل المتطابقات البارزة المكعبة. بالطبع، تعد صيغ الهوية المكعبة أكثر تعقيدًا بعض الشيء، ولكنها أيضًا مفيدة جدًا.
مكعب من المبلغ
المنتج المكعب الملحوظ للمجموع هو ذو الحدين (متعدد الحدود مع اثنين فقط من أحاديات الحد) أس 3 الذي يكون عنصراه موجبين. لذلك، جبريًا، يتم التعبير عن مكعب المجموع بالصيغة (a+b) 3 .
صيغة المساواة الملحوظة لمكعب المجموع هي:

بدءًا من ذات الحدين الموجبة المكعبة:
![]()
يمكن تحليل القوة المذكورة أعلاه إلى منتج العامل
![]()
بمربعها:
![]()
وبالمثل، كما رأينا في المعادلات التربيعية البارزة، ذات الحدين
![]()
يمكن حلها باستخدام صيغة مربع المجموع:
![]()
ثم نضرب كثيرتي الحدود معًا:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06771ecbb13542eae2a68477f849d729_l3.png)
أخيرًا، علينا فقط تجميع المصطلحات المتشابهة معًا:
![]()
وبالتالي يتم التحقق من صيغة الهوية البارزة لمجموع ذي الحدين المكعب:
![]()
باختصار، المجموع المرفوع إلى 3 يساوي مكعب الأول، بالإضافة إلى ثلاثة أضعاف مربع الأول في الثاني، بالإضافة إلى ثلاثة أضعاف الأول في مربع الثاني، بالإضافة إلى مكعب الثاني.
مثال:
- حل الهوية البارزة التالية للمجموع المكعب باستخدام الصيغة المقابلة لها:
![]()
في هذه المسألة لدينا ذات الحدين للقوة 3 التي يكون حداها موجبين. لذلك يجب علينا استخدام الصيغة لمجموع مكعب:
![]()
نحن الآن بحاجة إلى العثور على قيمة المعلمات
![]()
و
![]()
من الصيغة. في هذه الحالة،
![]()
تتوافق مع المتغير
![]()
و
![]()
هو رقم 2.
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-909b3b4a2f976c165f160a6765b3ed9d_l3.png)
والتي نحسب بها المنتج البارز عن طريق استبدال قيم
![]()
وبناءا على
![]()
في الصيغة:

مكعب الفرق
مكعب الفرق ، أو مكعب الطرح ، هو ذات حدين للقوة 3 وله حد ذو إشارة سالبة. لذا، فإن التعبير الرياضي لهذا النوع الرائع من المنتجات هو (ab) 3 .
صيغة مكعب الفرق (أو الطرح) هي:

من الواضح أن إثبات هذه الصيغة يشبه إلى حد كبير إثبات حاصل الضرب البارز للمجموع المكعب. لكن في هذه الحالة، نبدأ من ذات الحدين المكعب السالب:
![]()
من الواضح أن التقوية السابقة يمكن أن تتحلل إلى منتج العامل
![]()
مضروبًا في مربعه:
![]()
إذن، كما درسنا في المتطابقات المربعة البارزة، ذات الحدين
![]()
ويمكن حسابه باستخدام صيغة مربع الفرق:
![]()
نحن الآن ننتج حاصل ضرب كثيرتي الحدود:
![Rendered by QuickLaTeX.com \begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-627a273de8fff974f4a14a32fcee90b8_l3.png)
والخطوة الأخيرة هي تجميع المصطلحات المتشابهة:
![]()
وبالتالي يتم التحقق من صيغة الهوية البارزة لطرح ذات الحدين المرفوعة إلى المكعب:
![]()
إذن فإن الفرق (أو الطرح) مرفوعًا إلى ثلاثة يساوي مكعب الأول، ناقص ثلاثة أضعاف مربع الأول على الثاني، بالإضافة إلى ثلاثة أضعاف الأول على مربع الثاني، ناقص مكعب الثاني.
مثال:
- احسب ذات الحدين المكعبين (الفرق) التالي باستخدام الصيغة المقابلة لها:
![]()
في هذا التمرين، لدينا زوج يحتوي على عنصر إيجابي وعنصر سلبي. لذلك يجب علينا استخدام صيغة الفرق المكعب:
![]()
أولاً، كما هو الحال دائمًا، نحدد قيمة المجهول
![]()
و
![]()
من الصيغة. في هذه الحالة
![]()
يمثل أحادي الحد
![]()
و
![]()
هو المصطلح المستقل ذو الحدين، أي 2.
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a792ec6dead8466ec6a2cb2a43d9fab4_l3.png)
لاحظ أن المعلمة
![]()
ببساطة يساوي 2، بدون إشارة الرقم السالبة. من المهم أن تضع ذلك في الاعتبار لتطبيق الصيغة بشكل صحيح.
وأخيراً نجد الهوية الرائعة من خلال وضع قيم
![]()
وبناءا على
![]()
في الصيغة:

جدول ملخص للهويات البارزة
باختصار، لقد قمنا بإنشاء جدول يضم جميع الهويات (أو المنتجات) البارزة التي رأيناها، لذلك سيكون من الأسهل عليك دراستها. 😉

تمارين محلولة للهويات (أو المنتجات) البارزة
حتى تنتهي من فهم مفهوم الهويات الرائعة، والتي تسمى أيضًا المنتجات الرائعة أو المساواة الرائعة، قمنا بإعداد العديد من التمارين التي تم حلها خطوة بخطوة. يمكنك محاولة القيام بها ثم التحقق مما إذا كنت قد قمت بعمل جيد في حل التمارين.
⬇⬇ لا تنسوا أنه بإمكانكم طرح جميع أسئلتكم أدناه في التعليقات! ⬇⬇
التمرين 1
قم بتوسيع الهويات البارزة التالية (مجموع المربعات):
![]()
![]()
![]()
![]()
جميع المتطابقات البارزة في المشكلة عبارة عن مجاميع مربعة، لذلك في هذه الحالة يجب علينا دائمًا تطبيق نفس الصيغة:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-067fdf38612ca481db587bda479cab24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
تمرين 2
تطوير المنتجات البارزة التالية (تربيع الاختلافات):
![]()
![]()
![]()
![]()
جميع المنتجات البارزة في هذا التمرين هي عمليات طرح مربعة، لذلك نحتاج فقط إلى تطبيق صيغة واحدة:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14d502eda968fe82617b4403cd9c4722_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c22d520301280872e645f5683a2fba8e_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95c7c481a96b20b700bd2253c90f0c0d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cea9fa89580d3d9d9df7fd93cca2b89_l3.png)
التمرين 3
قم بتطوير المساواة الملحوظة التالية (منتجات المبالغ بالاختلافات):
![]()
![]()
![]()
![]()
نظرًا لأن جميع المعادلات الملحوظة في هذا التمرين عبارة عن ضرب المجاميع في الفروق، فقد تم حلها جميعًا بنفس الصيغة:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-826c4aec8f005514a14cdc8555c084c4_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6793239af84413fb9408c2cb6033e5ce_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-630b94cf4be27c5f7b9c87651368634d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-80c5451e407a2c0e670c6cb22a74043c_l3.png)
التمرين 4
حل جميع الهويات البارزة التالية:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c65875e01d82840e30ae85d803d45e90_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04e0bcf5df362d320cfdb2f87cdc6ddc_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc3f7dc61f7c44a60c01e0a95de278fa_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4d4a0c86d26820881eb65cb92c3679a_l3.png)
![Rendered by QuickLaTeX.com \text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-432c4ae0f050bec15e3fa52f426698ec_l3.png)
التمرين 5
احسب المنتجات البارزة التالية:
![]()
![]()
![]()
![]()
للعثور على جميع نواتج المسألة البارزة، من الضروري تطبيق صيغ المجموع والفرق المكعب وفقًا للحالات:
![]()
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14695fb807e2df89352fdd1c1dced2ee_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5be0d584351feb0bef5572ca5c9e159a_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44f9c3283dad97321644c6e559f64ff_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-156e7619e4d6ef129f04250af8197d2e_l3.png)
التمرين 6
حل المعادلات الملحوظة التالية:
![]()
![]()
![]()
![]()
لحل كل هذه المتطابقات البارزة، نحتاج إلى استخدام صيغة مربع ثلاثية الحدود، وهي:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-749dc45e7a00d7122d62b774706bdcc0_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1f51f18b3c1118b6e8e3acc3441b0ec_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-49c6496bf684296d315fc96d9cb5857e_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7cd08035d8402c27c411bcf5b30216cb_l3.png)
التمرين 7
احسب الهويات البارزة التالية مع الجذور والكسور (صعوبة عالية):
![]()
![]()
![]()
![]()
القسم أ) يتكون من طرح مربع، لذا لحلها يجب تطبيق الصيغة المقابلة لها، بالإضافة إلى ذلك، يجب أن نتذكر أنه إذا تم تربيع الجذر، فسيتم تبسيطه:
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-999e71bf062ea313780439abaf2b4295_l3.png)
القسم ب) يتعامل مع الجمع بالطرح ووحيدات الحد لها معاملات كسرية، والتي يجب تحديد هذا المنتج البارز باستخدام صيغة الجمع بالطرح وخصائص الكسور:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-24593bac7bd4a9837e1f18fef4f9c38e_l3.png)
المساواة الملحوظة في القسم ج) عبارة عن مجموع مرفوع إلى 2، وبالمثل، يتكون من كسور. لذلك، لحسابه نحتاج إلى استخدام صيغة المجموع التربيعي بالإضافة إلى خصائص الكسور:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
المتطابقة البارزة الأخيرة تتعامل مع مجموع ضرب الفرق بمعاملات غير منطقية، لذلك نطبق صيغة المجموع ضرب الفرق ثم نبسط الجذور التربيعية:
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c540e4315e9e84faaa2ff656c4eec21_l3.png)
أنواع الهوية البارزة الأخرى
جميع الهويات البارزة التي ناقشناها أعلاه هي الأكثر استخدامًا. ومع ذلك، في الرياضيات هناك أنواع أخرى من المنتجات البارزة والتي من المثير للاهتمام أيضًا معرفتها، حيث يتم استخدامها لأغراض مختلفة.
مجموع المكعبات
مجموع المكعبات يتوافق مع ذات الحدين التي يكون حداها موجبين، علاوة على ذلك، جذورها التكعيبية دقيقة. وبالتالي فإن التعبير الجبري لمجموع المكعبات هو a 3 +b 3 .

يتم استخدام صيغة هذا المنتج البارز لتحليل كثيرة الحدود، أي أنه من خلال الصيغة نقوم بتحويل كثيرة الحدود إلى حاصل ضرب ذات الحدين في ثلاثية الحدود.
حتى تتمكن من رؤية كيف يتم ذلك، إليك مثال لتطبيق هذه الهوية الرائعة:
![]()
في الواقع، التعبير السابق يتكون من جمع مكعبات لأن الجذر التكعيبي لأحادية الحد
![]()
دقيق (لا يعطي رقمًا عشريًا) والرقم 8 أيضًا:
![]()
![]()
![]()
لذلك، يمكننا استخدام صيغة مجموع المكعبات الكاملة لتحويل التعبير المكعب إلى حاصل ضرب ذات الحدين في ثلاثي الحدود:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f30ea5f0f7ef1b89a16f1d00e54d063c_l3.png)
اختلاف المكعبات
الفرق (أو الطرح) بين المكعبات هو ذات الحدين يتكون من حد موجب وحد سالب جذورهما المكعبة دقيقة. بمعنى آخر، يتم التعبير عن الفرق بين المكعبات بالشكل a 3 -b 3 .

لنضرب مثالاً حتى تتمكن من رؤية كيفية حل نوع الهوية الرائع هذا:
![]()
وهو اختلاف بين المكعبات لأن كلا من الجذر التكعيبي لأحادية الحد
![]()
حيث أن 27 صحيحة:
![]()
![]()
![]()
يمكنك بالتالي استخدام صيغة الفرق بين المكعبات الكاملة لتحليل ذات الحدين:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-342a448f849bf2856ad9a5394733faeb_l3.png)
منتج ذو الحدين بمصطلح مشترك
يتم استخدام هذا المنتج البارز لتحويل منتج اثنين من الحدين لهما مصطلح مشترك إلى كثيرة الحدود من الدرجة الثانية.

فيما يلي مثال تفصيلي لهذا النوع من المنتجات الرائعة:
![Rendered by QuickLaTeX.com \begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8447db6a2246c09b2e7be29f8050a3d6_l3.png)
المزيد من الهويات
وعلى الرغم من أن الهويات البارزة هي الأكثر شهرة لأنها الأكثر شيوعًا، إلا أنه تجدر الإشارة إلى أن هناك هويات أكثر بأسماء أخرى أيضًا. فيما يلي قائمة بالهويات الأخرى الأقل شهرة في حالة فضولك:
- هويات لاغرانج:
-
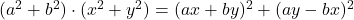
-
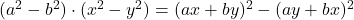
- الهويات الأسطورية:
-
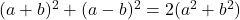
-
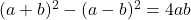
-
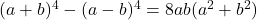
- هوية أرجاند:
-
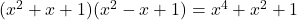
- الهويات الغوسية:
-
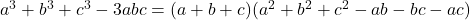
-
![Rendered by QuickLaTeX.com a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6b2da7d99ade85355a54bee45b79a9f_l3.png)
تطبيقات الهوية البارزة
إذا وصلت إلى هذا الحد، فهذا يعني أنك تعرف بالفعل كيفية إجراء العمليات الحسابية باستخدام الهويات البارزة. ساطع! لكن في الحقيقة… ما هي الهويات البارزة؟ ومتى يتم استخدام الهويات البارزة؟
كما رأينا خلال هذه المقالة، فإن الغرض الرئيسي من الهويات البارزة هو تبسيط الحسابات. وهذا يعني أنه بفضل المنتجات الرائعة، يمكننا حل قوى معينة لكثيرات الحدود المعقدة بشكل مباشر دون الحاجة إلى إجراء عمليات صعبة.
لكن التساويات الملحوظة لها أيضًا وظائف أخرى، مثل تحليل كثيرات الحدود وإكمال المربعات. ثم سنرى مما يتكون كل من هذه التطبيقات.
تحليل كثيرات الحدود
يمكن تحليل بعض الأنواع المحددة جدًا من كثيرات الحدود بمتطابقات بارزة. على سبيل المثال، إذا وجدنا كثيرة حدود مكونة من حدين يمثلان مربعين كاملين (جذورهما التربيعية دقيقة)، فيمكننا تحليلها باستخدام صيغة المساواة الرائعة لحاصل ضرب المجموع في الفرق:
![]()
![]()
وبالمثل، يمكن تحليل ثلاثيات الحدود التي تحترم الهويات البارزة لمربع الجمع أو الطرح:
![]()
![]()
![]()
![]()
وبالمثل، بمجرد تحليل كثيرة الحدود، يمكن العثور على جذور (أو أصفار) تلك كثيرة الحدود. ومع ذلك، فإن فهم هذا المفهوم أكثر تعقيدًا بعض الشيء، لذا إذا كنت مهتمًا أكثر، نوصي بالبحث عن الشرح في محرك البحث على موقعنا (أعلى اليمين)، حيث لدينا مقال كامل يشرحه.
إكمال المربع
إكمال المربعات هو إجراء رياضي يستخدم لتحويل ثلاثية الحدود من الدرجة الثانية إلى مجموع مربع زائد (أو ناقص) رقم.
بالنظر إلى أي ثلاثية الحدود:
![]()
ومن ثم يمكن تحويل ثلاثي الحدود إلى التعبير التالي:
![]()
حيث المعلمات
![]()
و
![]()
يتم حسابها باستخدام الصيغ التالية:
![]()
حتى لو لم يبدو الأمر كذلك بالنسبة لك، فقد تم استنتاج هاتين الصيغتين من هويات بارزة. لذلك، بفضل المنتجات الرائعة، يمكن إكمال المربعات.
على سبيل المثال، سوف نطبق هذا الإجراء على ثلاثية الحدود التالية:
![]()
نحن نحسب المعلمات
![]()
و
![]()
![]()
![]()
وبالتالي تبقى كثيرة الحدود:
![]()