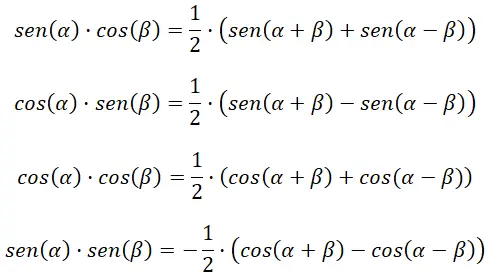ما هي الهويات المثلثية؟

الهويات المثلثية هي مساواة بين الدوال المثلثية المختلفة. وبفضل هذه المعادلات المثلثية، يمكننا استنتاج نسبة مثلثية معينة بناءً على أي نسبة مثلثية أخرى. ولذلك فمن الضروري معرفة صيغ هذه النسب لفهم صيغ المتطابقات المثلثية. إذا كنت لا تعرفهم في حالتك، فننصحك بزيارة الرابط الأخير.

جدول الهويات المثلثية

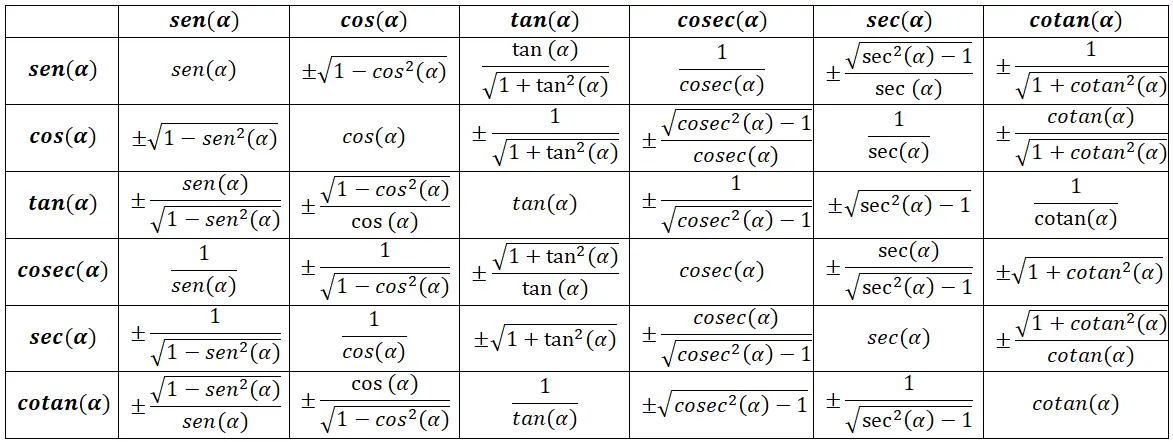
الهويات المثلثية الأساسية

هناك سلسلة من الهويات المثلثية الأساسية التي تعتبر الأكثر أهمية لأنها توفر الأساس النظري للآخرين. هذه هي الأكثر شيوعًا والتي من المحتمل أن تكون الأسهل في التذكر، لأنها بديهية تمامًا. تذكر أن جميع الصيغ سوف تعتمد على الصورة التالية:

الهوية المثلثية الأساسية

الهوية الأولى للجميع هي ما يعرف بالهوية المثلثية الأساسية ، والمعروفة أيضًا بالعلاقة بين الجيب وجيب التمام. فيما يلي برهانها الرياضي: sin² (α) + cos² (α) = 1.

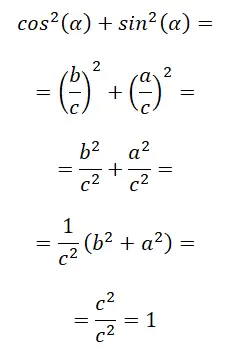
في الخطوة الأخيرة، نطبق بشكل أساسي نظرية فيثاغورس، لأن c² = a² + b²، يتبقى لدينا c² / c² وهو ما يساوي 1. في الختام، يمكننا أن نذكر أن: sin² (α) + cos² (α) = 1.

العلاقة بين القاطع والظل (القاطع التربيعي)

ثانيًا، لدينا هوية مثلثية تربط القاطع بالظل، ويكون تعبيرها كما يلي: sec² (α) = 1 + tan² (α) . في الصورة التالية يمكنك رؤية بعض صيغ التذكير التي تشكل هذه الهوية ومن ثم الإجراء الذي يجب اتباعه للوصول إلى الصيغة النهائية:

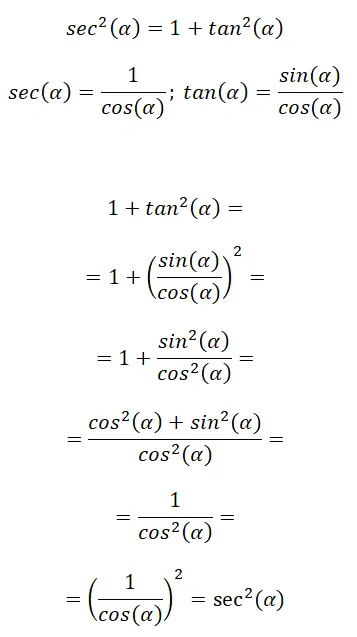
في هذه الحالة، نستخدم صيغ النسبة المثلثية للعثور على نسب أخرى. في الختام يمكننا القول أن: sec²(α) = 1 + tan²(α).

العلاقة بين قاطع التمام وظل التمام (مربع قاطع التمام)

من تعريف قاطع التمام وظل التمام يمكننا العثور على رابط في صيغة الظل، وبفضل هذا يمكننا استنتاج هوية مثلثية أخرى: cosec² (α) = 1 + cotg² (α) .

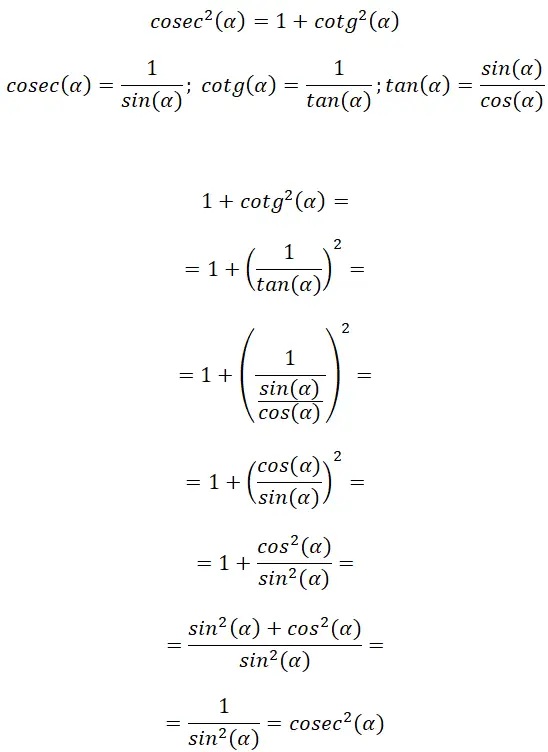
من خلال هذا العرض التوضيحي يمكننا التحقق من أن: cosec² (α) = 1 + cotg² (α). بالإضافة إلى ذلك، يمكننا أن نرى أن هذه العلاقة بها بعض التشابه مع العلاقة السابقة، وذلك بسبب التشابه بين ظل الزاوية وظل التمام.

النسب المثلثية لزاوية مجموع وزاوية الطرح

مجموع الزوايا أو نسب طرح الزاوية هي نوع من الهويات التي يتم الحصول عليها عن طريق حساب النسب المثلثية لجمع أو طرح زاويتين. على سبيل المثال، إذا أردنا حساب جيب الزاوية 90 + 60، فهناك سلسلة من الصيغ التي تجعل هذا الحساب أسهل. فيما يلي قائمة بجميع الصيغ الخاصة بالهويات المثلثية لهذا النمط:

جيب مجموع الزوايا: sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )

جيب الزاوية للطرح: sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )

جيب تمام مجموع الزوايا: cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )

طرح جيب التمام الزاوي: cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )

ظل مجموع الزوايا: tan (α + β ) = (tan (α) + tan ( β )) ÷ (1 – tan (α) tan ( β ))

طرح المماس الزاوي: tan(α – β ) = (tan(α) + tan( β )) ÷(1 + tan(α)tan( β ))

من الواضح أن حساب جيب الزاوية 150 درجة أسهل من استخدام الصيغ التي شرحناها للتو لحساب جيب الزاوية (90 درجة + 60 درجة). فلماذا تعتبر هذه الصيغ مهمة؟ حسنًا، الإجابة هي أن هذه المتطابقات تتيح لنا حساب النسب المثلثية للزوايا المعقدة من زوايا أبسط. لذلك، إذا حفظنا نسب الزوايا البارزة (الأكثر صلة)، فلن نحتاج إلى استخدام الآلة الحاسبة لحساب نسب الزوايا الأكثر تعقيدًا مثل 150 درجة.

النسب المثلثية للزاوية المزدوجة

عندما نريد حساب النسب المثلثية لزاوية مزدوجة (2α) يمكننا القيام بذلك عن طريق سلسلة من المتطابقات. وبشكل أكثر دقة، يمكننا القيام بذلك من خلال صيغ مشابهة جدًا لتلك التي ناقشناها للتو في القسم السابق. لأنه إذا قمنا بتغيير β إلى α، في التعبيرات السابقة، يتبقى لدينا (α + α)، وهو ما يعادل (2α). ومن هذا المنطلق يمكننا أن نستنتج الهويات التالية:

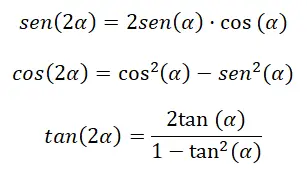
يمكنك مشاهدة العروض التوضيحية أدناه:

جيب الزاوية المزدوجة: sin (2α) = sin (α) cos (α) + cos (α) sin (α) = 2 sin (α) cos (α)

جيب تمام الزاوية المزدوجة: cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)

زاوية الظل المزدوجة: ظا (2α) = 2 ظا (α) ÷ (1 – ظا² (α))

النسب المثلثية لنصف الزاوية

كما أن هناك هويات تسمح لنا بحساب النسب المثلثية لنصف الزاوية (α/2) :

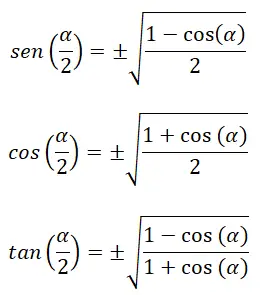
من بين الصيغ المعروفة بالفعل التالية:

1 = الخطيئة²( β ) + cos²( β )

cos( 2β ) = cos²( β ) – الخطيئة²( β )

إذا جعلنا β = α/2، فيمكننا إثبات هذه المتطابقات، عن طريق طرح التعبيرين في حالة جيب التمام، وإضافتهما في حالة جيب التمام، وتقسيم الصيغتين الناتجتين (صيغة الجيب وجيب التمام) في حالة الظل. ومع ذلك، يبقى عزل النسبة التي نريد حسابها في الصيغ التي نحصل عليها أدناه:

نصف زاوية جيبية: 1 – cos (α) = 2 sin² (α/2)؛ خطيئة² (α/2) = (1 – جتا (α)) ÷ 2

جيب تمام نصف الزاوية: 1 + cos (α) = 2 cos² (α/2)؛ cos² (α/2) = (1 + cos (α)) ÷ 2

النسب المثلثية للزاوية الثلاثية

في حالة وجود زاوية ثلاثية (3α) يمكننا أيضًا استخدام هويات معينة لحساب نسبها المثلثية. تأتي هذه الهويات من الصيغ التالية التي سبق شرحها: هويات الزاوية المزدوجة، وهويات مجموع الزوايا، والهوية الأساسية لعلم المثلثات.

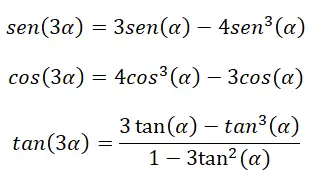
لإثبات هذه المتطابقات، يجب علينا استخدام صيغ مجموع الزوايا:

جيب مجموع الزوايا: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)

جيب تمام مجموع الزوايا: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)

لذا، إذا طبقنا صيغ الزاوية المزدوجة في التعبيرات التي تحدثنا عنها للتو وطبقنا المتطابقة الأساسية لعلم المثلثات، فيمكننا إثبات المتطابقات. ومن الجدير بالذكر أن استخدام المتطابقة المثلثية الأساسية يسمح لنا بتحويل جميع النسب في التعبير إلى نسبة واحدة. هذا هو السبب في أن صيغة جيب الزاوية الثلاثية تتكون فقط من الجيب وأن صيغة جيب التمام تحتوي على جيب التمام فقط. أدناه يمكنك رؤية الإجراء الكامل:

جيب الزاوية الثلاثية: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α) =

= الخطيئة (α) (cos² (α) – الخطيئة² (α)) + 2 الخطيئة (α) cos (α) cos (α) =

= الخطيئة (α) cos² (α) – الخطيئة³ (α) + 2 الخطيئة (α) cos² (α) =

= الخطيئة (α) · (1 – الخطيئة² (α)) – الخطيئة³ (α) + 2 الخطيئة (α) · (1 – الخطيئة² (α)) =

= الخطيئة (α) – الخطيئة³ (α) – الخطيئة³ (α) + 2 الخطيئة (α) – 2 الخطيئة³ (α) =

= 3 خطيئة (α) – 4 خطيئة³ (α)

جيب تمام الزاوية الثلاثية: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =

= cos (α) (cos² (α) – sin² (α)) – sin (α) 2 sin (α) cos (α) =

= cos³ (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =

= cos³ (α) – 3 cos (α) sin² (α) =

= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =

= cos³ (α) – 3 cos (α) + 3 cos³ (α) =

= 4 كوس³ (α) – 3 كوس (α)

أخيرًا، يمكن حساب ظل الزاوية الثلاثية بطريقتين: الأولى عن طريق قسمة صيغة الجيب على صيغة جيب التمام والثانية عن طريق استبدال تعبير ظل الزاوية المزدوجة في الصيغة التالية إلى ظل الزاوية مجموع الزاوية: تان (α + 2α) = (تان (α) + تان (2α)) ÷ (1 – تان (α) تان (2α)).

الهويات المثلثية حسب نوع الزاوية

من المهم التعليق على سلسلة من الصيغ التي هي بطريقة ما قواعد تسمح بالحساب المباشر والسريع للنسب المثلثية. في الواقع، يمكن أيضًا اعتبارها متطابقات مثلثية، لأنها تلبي نفس خصائص جميع التعبيرات التي تحدثنا عنها للتو. وبشكل أكثر دقة، تسمح لنا هذه الصيغ بتحديد العلاقات المثلثية للزاوية من العلاقة التي تربطها بزاوية أخرى.

زوايا متكاملة

الزاويتان المتتامتان (α و β ) هي تلك التي مجموع قياساتها يساوي 90 درجة، لذلك عندما نضيفها نحصل على زاوية قائمة. لتحديد أن α هي الزاوية المكملة لـ β ، يجب أن نحل معادلة بسيطة للغاية: α = 90 – β ، فإذا اتفقت نتيجة هذا التكافؤ، يمكننا أن نؤكد أنهما متكاملتان. وبفضل هذه المتطابقات يمكننا استنتاج النسب المثلثية لزاوية واحدة من تلك الخاصة بالأخرى.

جيب الزاوية التكميلية: sin (90° – α) = cos (α)

جيب تمام الزاوية التكميلية: cos (90° – α) = sin (α)

ظل الزاوية التكميلية: ظا (90° – α) = كوتان (α)

قاطع التمام للزاوية التكميلية: cosec (90° – α) = sec (α)

قاطع الزاوية التكميلية: ثانية (90 درجة – α) = cosec (α)

ظل التمام للزاوية التكميلية: كوتان (90 درجة – α) = تان (α)

زوايا إضافية

الزوايا التكميلية (α و β ) هي تلك التي يبلغ مجموعها 180 درجة أو π راديان، وبالتالي يمكننا استنتاج الصيغة α + β = 180 درجة. أو بمعنى آخر، إذا كانت الزاوية التكميلية لـ α هي β ، فيجب تحقيق التعبير التالي β = 180 – α . ثم يمكنك رؤية قائمة الهويات التي يمكننا استنتاجها من هذه الزوايا:

جيب الزاوية التكميلية: sin (180° – α) = sin (α)

جيب تمام الزاوية الإضافية: cos (180° – α) = -cos (α)

ظل الزاوية التكميلية: tan (180° – α) = -tan (α)

قاطع التمام للزاوية الإضافية: cosec (180° – α) = cosec (α)

قاطع الزاوية التكميلية: ثانية (180 درجة – α) = – ثانية (α)

ظل التمام للزاوية التكميلية: كوتان (180 درجة – α) = -كوتان (α)

زوايا مترافقة

الزوايا المترافقة (α و β ) هي تلك التي يبلغ مجموعها 360 درجة أو 2π راديان، ولهذا السبب يمكننا استنتاج الصيغة α + β = 360 درجة. ومن هذه الصيغة الأولى يمكننا التعبير عن إحدى الزوايا بدلالة الأخرى كما يلي: α = 360° – β أو β = 360° – α. سنوضح لك الآن تساوي الزوايا المترافقة:

جيب الزاوية المرافقة: sin (360° – α) = – sin (α)

جيب تمام الزاوية المرافقة: cos (360° – α) = cos (α)

ظل الزاوية المرافقة: ظا (360° – α) = – ظا (α)

قاطع تمام الزاوية المرافقة: cosec (360° – α) = – cosec (α)

قاطع الزاوية المرافقة: ثانية (360 درجة – α) = ثانية (α)

ظل التمام للزاوية المرافقة: كوتان (360 درجة – α) = – كوتان (α)

زوايا متضادة

الزوايا المتقابلة أو الزوايا السالبة (α و β ) هي تلك التي لها نفس القيمة العددية، ولكن لها إشارات مختلفة، مثال على هذا النوع من الزوايا هو 30 درجة و -30 درجة. يجب أن نتذكر أن الإشارة السالبة تشير إلى أن الدوران في اتجاه عقارب الساعة، بينما تدور الزاوية الموجبة عكس اتجاه عقارب الساعة.

جيب الزاوية المقابلة: الخطيئة (-α) = – الخطيئة (α)

جيب تمام الزاوية المقابلة: cos (-α) = cos (α)

ظل الزاوية المقابلة: ظا (-α) = – ظا (α)

قاطع التمام للزاوية المقابلة: cosec (-α) = – cosec (α)

قاطع الزاوية المقابلة: ثانية (-α) = ثانية (α)

ظل التمام للزاوية المقابلة: كوتان (-α) = – كوتان (α)

زوايا تختلف عن 90 درجة أو زوايا زائد/ناقص π/2

الزوايا التي تختلف بمقدار 90 درجة أو الزوايا زائد/ناقص π/2 (α و β ) هي تلك التي يبلغ الفرق فيها 90 درجة. ولذلك، يمكن التعبير عنها كـ β – α = 90°، حيث β أكبر بمقدار 90° من α . تحتوي هذه الزوايا أيضًا على سلسلة من الصيغ التي تربط النسب المثلثية للزاويتين.

جيب الزاوية التي تختلف عن 90°: sin (90° + α) = cos (α)

جيب تمام الزاوية التي تختلف عن 90°: cos (90° + α) = -sin (α)

ظل الزاوية التي تختلف عن 90 درجة: ظا (90 درجة + α) = – كوتان (α)

قاطع تمام الزاوية التي تختلف عن 90°: cosec (90° + α) = sec (α)

قاطع الزاوية التي تختلف عن 90 درجة: ثانية (90 درجة + α) = -cosec (α)

ظل التمام للزاوية التي تختلف عن 90 درجة: كوتان (90 درجة + α) = -كوتان (α)

زوايا تختلف عن 180 درجة أو زوايا زائد/ناقص π

الزوايا الزائدة/السالبة π (α و β ) تعادل الزوايا التي تختلف بمقدار 180 درجة. لذلك، يمكن التعبير عنها باستخدام الصيغة التالية: β – α = 180°، حيث β 180° أكبر من α . وبعد ذلك نعرض لك المتطابقات المثلثية التي تربط النسب المثلثية لهذه الزوايا:

جيب الزاوية التي تختلف عن 180°: sin (180° + α ) = -sin ( α )

جيب تمام الزاوية التي تختلف عن 180°: cos (180° + α ) = -cos ( α )

ظل الزاوية التي تختلف عن 180 درجة: ظا (180° + α ) = ظا ( α )

قاطع تمام الزاوية التي تختلف عن 180°: cosec (180° + α ) = -cosec ( α )

قاطع الزاوية التي تختلف عن 180°: sec (180° + α ) = -sec ( α )

ظل تمام الزاوية التي تختلف عن 180 درجة: كوتان (180 درجة + α ) = كوتان ( α )

تحويلات النسب المثلثية

وأخيرا، هناك متطابقات مثلثية تسمح لنا بالتعبير عن نسبة مثلثية معينة عن طريق عمليات أخرى . لذا، إذا كان لدينا مجموع النسب ونريد التعبير عنه كحاصل، فيمكننا اللجوء إلى هذه الصيغ. بالرغم من أنه للأسف لا يوجد تعبير لكل عملية حسابية، إلا أنه يمكنك فقط الانتقال من الجمع أو الطرح إلى المنتج والعكس .

تحويل الجمع أو الطرح إلى المنتج

تساعدنا الصيغ الأربع التالية في حساب جمع وطرح الدوال المثلثية:

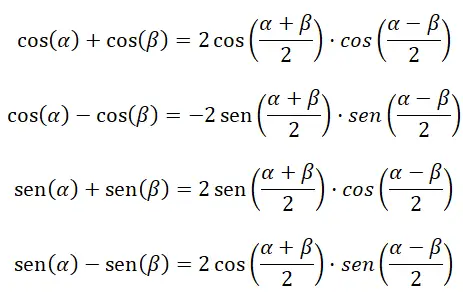
تحويل المنتج إلى الجمع أو الطرح

تساعدنا الصيغ الأربع التالية في حساب منتجات الدوال المثلثية: