الموقع النسبي لخطين في الفضاء

ستجد هنا جميع المواضع النسبية لخطين في الفضاء (في R3). بالإضافة إلى ذلك، فهو يشرح كيفية العثور على الموضع النسبي بين خطين باستخدام الطريقتين الممكنتين: عن طريق النطاقات أو من نقطة ومتجه لكل خط. ستتمكن أيضًا من رؤية الأمثلة والتمارين التي تم حلها خطوة بخطوة.

ما المواضع النسبية لخطين في الفضاء؟

في الهندسة التحليلية، عند العمل في مساحة ثلاثية الأبعاد (في R3) هناك 4 مواضع نسبية محتملة بين خطين: يمكن أن يكون الخطان عبارة عن خطوط مدمجة أو خطوط متوازية أو خطوط قاطعة أو خطوط قاطعة .

خطوط متوازية

يكون المستقيمان متوازيين إذا كان لهما نفس الاتجاه ولكن ليس بينهما نقطة مشتركة. بالإضافة إلى ذلك، الخطوط المتوازية تكون دائمًا على نفس المسافة من بعضها البعض.

خطوط متطابقة

يتطابق الخطان إذا كان لهما نفس الاتجاه، وعلاوة على ذلك، إذا كانت جميع نقاطهما مشتركة.

خطوط متقاطعة

خطان متقاطعان لهما اتجاهات مختلفة ولكنهما يتلامسان عند نقطة واحدة.

خطوط التقاطع

خطان متقاطعان لهما اتجاهات مختلفة ولا يتقاطعان في أي نقطة. ولذلك، فإن الخطين المتقاطعين ليسا في نفس المستوى. على سبيل المثال، في التمثيل الرسومي فوق السطر

$s$

هو دائما في المقدمة

$r$

، لذلك لن يلمسوا بعضهم البعض أبدًا.

هناك طريقتان لمعرفة الموضع النسبي بين خطين، حيث تعتمدان على كيفية التعبير عن معادلات الخطين:

إذا كانت الخطوط في شكل معادلة متجهة أو بارامترية أو مستمرة، فمن الأفضل حساب الموضع النسبي من نقطة ومتجه لكل خط (يرد شرح هذه الطريقة أدناه).
من ناحية أخرى، إذا تم تعريف الخطوط في شكل معادلات ضمنية (أو عامة)، فمن الأسهل معرفة الموقع النسبي بين الخطين عن طريق حساب رتبة المصفوفتين (انظر الشرح أدناه).

تحديد الموضع النسبي لخطين من نقطة ومتجه

يمكنك العثور على الموضع النسبي الموجود بين خطين بنقطة ومتجه لكل خط. تعتبر هذه الطريقة مناسبة للاستخدام عندما يتم تعريف الخطوط في شكل معادلة متجهة أو معادلات بارامترية أو معادلة مستمرة.

وبالتالي، فليكن متجه الاتجاه وأي نقطة على كل من الخطين:

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

لذا، للعثور على الموضع النسبي لخطين، علينا اتباع الإجراء التالي:

‣ أول شيء يتعين علينا القيام به هو معرفة ما إذا كانت متجهات الخطين متناسبة أم لا، وحسب الحالة، نقوم بما يلي:

إذا كان المتجهان متناسبين، فيمكن أن يكون المستقيمان متوازيين أو متطابقين. لذلك يجب علينا التحقق مما إذا كانت نقطة أحد الخطين تحقق معادلة الخط الآخر:
- إذا كانت نقطة أحد الخطين تحقق معادلة الخط الآخر، فهذا يعني أن الخطين متطابقان.
- وإلا فإنه يعني أن الخطين متوازيين.
إذا لم يكن المتجهان متناسبين، فيمكن أن تكون الخطوط متقاطعة أو متقاطعة. في هذه الحالة يجب علينا حل المحدد 3×3 التالي:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- إذا كان المحدد السابق يساوي الصفر، فإن الخطين يتقاطعان عند نقطة (يتقاطعان).
- إذا كان المحدد السابق مختلفا عن الصفر، فإن الخطين يتقاطعان.

الرسم التالي يلخص الإجراء بأكمله:

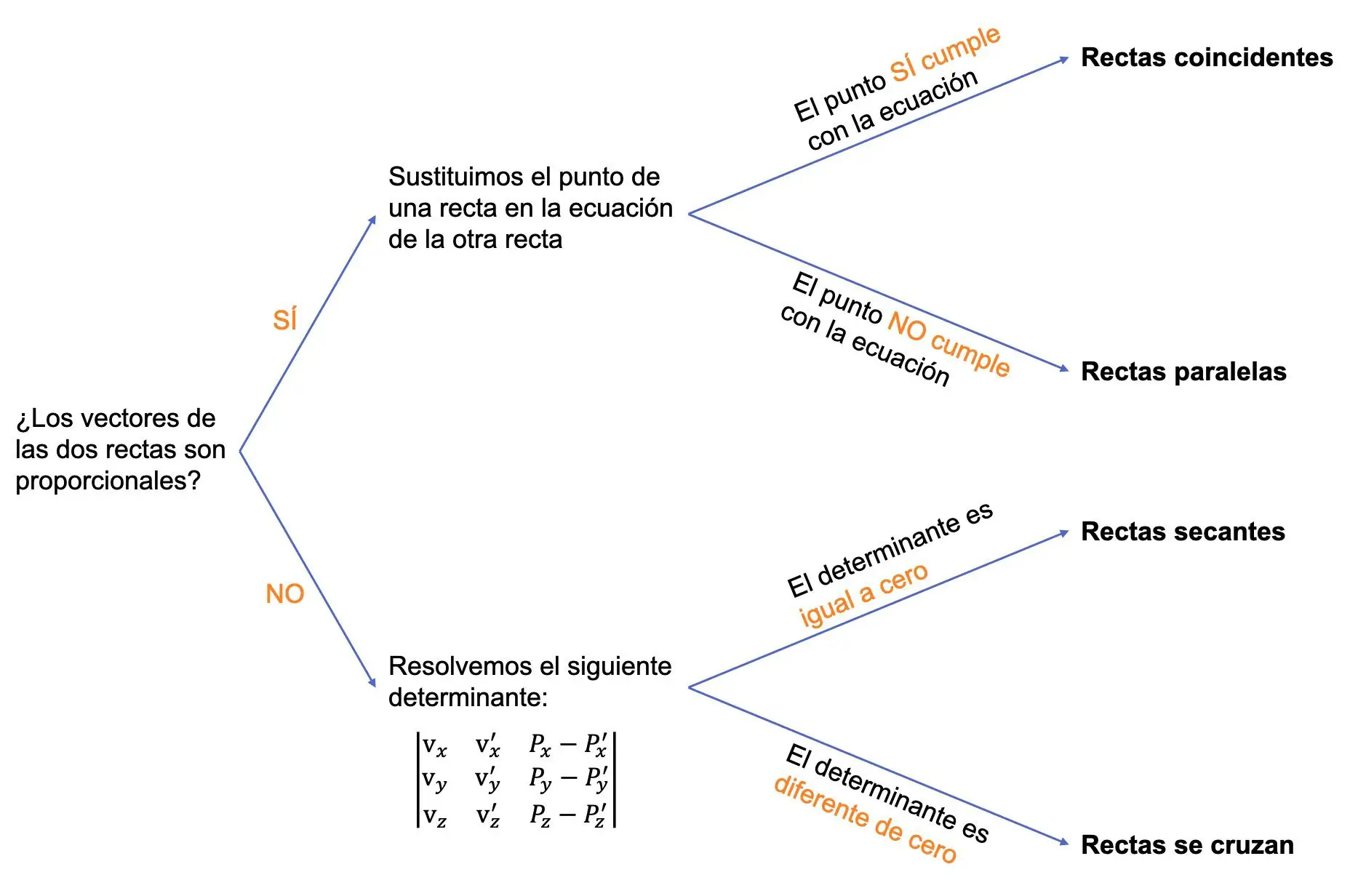
مثال على تحديد الموضع النسبي بين خطين

قد يبدو الإجراء السابق معقدًا بعض الشيء، لكن لكي ترى أن الأمر عكس ذلك، سنحل مشكلة كمثال:

حدد الموضع النسبي بين السطرين التاليين:

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

يتم التعبير عن الخطين كمعادلة متجهة، حيث يكون متجه الاتجاه لكل خط:

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

والنقطة التي يمر بها كل خط هي:

$R(2,0,1)\qquad \qquad S(1,-3,1)$

بمجرد أن نعرف نقطة ومتجه الاتجاه لكل خط، نطبق الطريقة الموضحة أعلاه. أولًا، يجب علينا التحقق مما إذا كانت إحداثيات المتجهات متناسبة:

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

نظرًا لأن المتجهين غير متناسبين مع بعضهما البعض، فإن الخطوط يمكن أن تتلامس أو تتقاطع مع بعضها البعض فقط. لذلك، علينا الآن إيجاد المحدد التالي الذي يتكون من متجه الاتجاه ونقطة على كل خط:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

نستبدل القيم في الصيغة:

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

ونحن نحسب المحدد، لذلك يمكنك استخدام أي طريقة (قاعدة ساروس، طريقة المكملات أو العوامل المساعدة، وما إلى ذلك):

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

ولو كانت نتيجة التحديد صفراً، فهذا يعني أن الخطوط متقاطعة (متلامسة). لكن المحدد يختلف عن 0، لذا تتقاطع الخطوط .

ابحث عن الموضع النسبي لخطين حسب الصفوف

هناك طريقة أخرى للعثور على الموضع النسبي لصفين وهي حساب رتب مصفوفتين ملموستين، كما سنرى بعد ذلك. هذه الطريقة مفيدة جدًا عندما يكون الخطان في صيغة معادلة ضمنية (أو عامة).

لذلك، إذا كان لدينا خطين معبرا عنهما بمعادلاتهما الضمنية (أو العامة) في فضاء ثلاثي الأبعاد (في R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

لتكن A هي المصفوفة المكونة من معاملات الخطين:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

وبالنظر إلى المصفوفة الموسعة A’، وهي المصفوفة المكونة من جميع معلمات الخطين:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

ومن ثم يمكن تحديد الموضع النسبي للصفين بمدى المصفوفتين السابقتين حسب الجدول التالي:

لذلك، للعثور على الموضع النسبي بين صفين، سيتعين علينا حساب رتب المصفوفتين، واعتمادًا على رتبة كل مصفوفة ستكون حالة أو أخرى.

يمكن إثبات هذه النظرية باستخدام نظرية روشيه-فروبينيوس (طريقة تستخدم لحل أنظمة المعادلات الخطية)، ولكن في هذه الصفحة لن نقوم بالبرهان لأنها مرهقة للغاية ولا تضيف الكثير.

مثال على كيفية العثور على الموضع النسبي لخطين حسب النطاقات

بمجرد أن رأينا نظرية المواضع النسبية بين سطرين تلو الآخر، دعونا نرى كيف يتم وضعها موضع التنفيذ من خلال مثال:

أوجد الموضع النسبي للسطرين التاليين:

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

الخطان على شكل معادلات عامة (أو ضمنية)، لذلك سنستخدم طريقة الرتب لإيجاد الموضع النسبي بين الخطين. لذلك نقوم ببناء المصفوفة A والمصفوفة الموسعة A’ بمعاملات الخطوط:

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

بمجرد حصولنا على كلتا المصفوفتين، نحتاج إلى حساب رتبة كل منهما. نحسب أولاً رتبة المصفوفة A بواسطة المحددات:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

تحتوي المصفوفة A على محدد المصفوفة الفرعية غير الصفرية 3×3، لذا فإن المصفوفة A لها الرتبة 3 .

والآن نحسب نطاق المصفوفة الموسعة A’. ستكون المصفوفة A’ دائمًا على الأقل في رتبة المصفوفة A، والتي في هذه الحالة تساوي 3، لذلك يكفي التحقق مما إذا كانت من الرتبة 4 أو من الرتبة 3. وللقيام بذلك، قمنا بحل المحدد من المصفوفة 4 × 4 عن طريق الإضافات (أو العوامل المساعدة):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

محدد المصفوفة الموسعة بأكملها هو صفر، وبالتالي فإن المصفوفة A’ هي أيضًا من المرتبة 3 .

إذن المصفوفة A و المصفوفة A’ من الرتبة 3 وبالتالي يتقاطع الخطان . أي أن هناك نقطة تقاطع واحدة فقط بينهما.

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

تذكر أن لديك جدولًا أعلاه يلخص جميع الحالات المحتملة للمواضع النسبية بين خطين وفقًا لنطاقات المصفوفات A وA’.

حل مسائل الموضع النسبي بين خطين في الفضاء

التمرين 1

أوجد الموضع النسبي بين السطرين التاليين:

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

انظر الحل

وبما أن كلا الخطين يتم التعبير عنهما كمعادلة متجهة، فسنجد الموضع النسبي بين الخطين بطريقة النقطة الواحدة والمتجه الواحد لكل خط.

متجه الاتجاه لكل خط هو:

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

والنقطة التي تنتمي إلى كل سطر هي:

$R(3,4,0)\qquad \qquad S(1,-2,2)$

وبالتالي، لتطبيق الإجراء، من الضروري أولاً التحقق مما إذا كانت مكونات متجهات الاتجاه متناسبة:

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

وبما أن المتجهين غير متناسبين مع بعضهما البعض، فلا يمكن أن تكون الخطوط متقاطعة أو متقاطعة إلا. لذلك، علينا الآن إيجاد المحدد التالي الذي يتكون من متجه الاتجاه ونقطة على كل خط:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

نستبدل القيم في الصيغة:

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

ونحسب المحدد :

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

نتيجة المحدد تعادل 0، وبالتالي فإن الخطوط تتقاطع .

تمرين 2

احسب الموضع النسبي للسطرين التاليين:

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

انظر الحل

السطر الأول على شكل معادلات بارامترية والسطر الثاني على شكل معادلة متصلة، والتي سنحدد بها الموضع النسبي بين الخطين بطريقة النقطة الواحدة المتجه لكل خط.

إحداثيات متجه الاتجاه لليمين

$r$

هي المعاملات أمام المعلمة

$t,$

وإحداثيات متجه الاتجاه للخط

$s$

هي أرقام القواسم:

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

والنقطة التي تنتمي إلى كل سطر هي:

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

وبالتالي، لتطبيق الإجراء، من الضروري أولاً التحقق مما إذا كانت مكونات متجهات الاتجاه متناسبة:

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

المتجهان متناسبان مع بعضهما البعض، لذلك لا يمكن أن تكون الخطوط متوازية أو متطابقة إلا. ولإزالة هذا الشك، من الضروري استبدال النقطة الموجودة على السطر

$r$

في معادلة الخط

$s$

(أو العكس) لمعرفة ما إذا كانت تفي بالمعادلة المذكورة:

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

من خلال استبدال النقطة الموجودة في الخط نحصل على المساواة، بحيث تحقق نقطة أحد الخطين معادلة الخط الآخر، علاوة على ذلك، تكون متجهات اتجاههما متناسبة. ولذلك فإن الخطين متطابقان.

التمرين 3

أوجد الموضع النسبي للسطرين التاليين:

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

انظر الحل

الخطان في صيغة معادلة عامة (أو ضمنية)، لذا سنستخدم طريقة الترتيب للعثور على الموضع النسبي بين الخطين. لذلك نجعل المصفوفة A والمصفوفة الموسعة A’ بمعاملات الخطوط:

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

بمجرد حصولنا على كلتا المصفوفتين، نحتاج إلى حساب رتبة كل منهما. نحسب أولاً رتبة المصفوفة A بواسطة المحددات:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

جميع محددات 3×3 للمصفوفة A هي صفر، ولكن هناك محددات 2×2 غير صفرية داخل المصفوفة، لذا فإن المصفوفة A لها الرتبة 2 .

والآن نحسب نطاق المصفوفة الموسعة A’. ستكون المصفوفة A’ دائمًا على الأقل مدى المصفوفة A، والتي في هذه الحالة هي 2، لذلك من الضروري التحقق مما إذا كانت تحتوي على محدد 3×3 لا يمكن إلغاؤه وأيضًا مقدار محدد المصفوفة بأكملها:

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

تحتوي المصفوفة الموسعة A’ بالفعل على 3 × 3 محددات فرعية غير صفرية، وعلاوة على ذلك، فإن محدد المصفوفة الموسعة بأكملها يساوي 0، وبالتالي فإن المصفوفة A’ لها المرتبة 3 .

إذن المصفوفة A من الرتبة 2 والمصفوفة A’ من الرتبة 3، لذا فإن الخطين متوازيان . وهذا يعني أنه ليس لديهم أي شيء مشترك.

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

تذكر أنه في شرح الطريقة (أعلاه) لديك جدول يلخص جميع الحالات المحتملة للمواضع النسبية بين خطين حسب رتب المصفوفتين A وA’.

التمرين 4

أوجد الموضع النسبي للسطرين التاليين:

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

انظر الحل

في هذه الحالة، يكون الخطان في صيغة المعادلة الديكارتية (أو الضمنية)، لذلك سنستخدم طريقة الترتيب للعثور على الموضع النسبي بين الخطين. لذلك نقوم ببناء المصفوفة A والمصفوفة الموسعة A’ بمعاملات الخطوط:

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

بمجرد أن نعرف المصفوفتين، نحتاج إلى حساب رتبة كل منهما. سنقوم أولاً بحساب رتبة المصفوفة A بواسطة المحددات:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

تحتوي المصفوفة A على مصفوفة فرعية 3×3 محددها غير صفر، لذا فإن المصفوفة A لها الرتبة 3 .

والآن نحسب نطاق المصفوفة الموسعة A’. ستكون المصفوفة A’ دائمًا على الأقل من رتبة المصفوفة A، والتي في هذه الحالة تساوي 3، لذا يكفي التحقق مما إذا كانت من الرتبة 4 أو من الرتبة 3. وللقيام بذلك، قمنا بحل محدد مجموعة المصفوفة 4×4 بالإضافات (أو العوامل المساعدة):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$