الموقع النسبي لخطين في الطائرة

ستجد في هذه الصفحة شرحًا للطرق المختلفة الموجودة لتحديد الموضع النسبي لخطين في المستوى (في R2). بالإضافة إلى ذلك، سترى العديد من الأمثلة وستكون قادرًا على التدرب على التمارين التي تم حلها خطوة بخطوة.

ما هو الموقع النسبي لخطين في الطائرة؟

قبل النظر إلى المواضع النسبية بين خطين في المستوى، من الواضح أنك بحاجة إلى معرفة ما هو الخط بالضبط، ويمكنك العثور عليه في تعريف الخط .

وبالتالي، عند العمل في بعدين (في R2)، هناك 3 أنواع من المواضع النسبية المحتملة بين خطين:

ومن ناحية أخرى، فإن الزاوية بين خطين في المستوى تعتمد أيضًا على موضعهما النسبي:

• تتقاطع الخطوط المتقاطعة بزاوية تتراوح بين 0 درجة (غير مدرجة) و90 درجة (شاملة). بالإضافة إلى ذلك، إذا كانا يشكلان زاوية قائمة تبلغ 90 درجة فقط، فهذا يعني أن الخطين متعامدان.
• تشكل الخطوط المتوازية زاوية مقدارها 0 درجة، لأنها لها نفس الاتجاه.
• وللسبب نفسه، تشكل الخطوط المتطابقة أيضًا زاوية مقدارها 0 درجة بينهما.

إذا كنت تريد معرفة كيفية حساب الزاوية بين خطين، يمكنك التحقق من صيغة الزاوية بين خطين . ستجد هنا شرحًا تفصيليًا لكيفية تحديد الزاوية بين خطين، بالإضافة إلى العديد من الأمثلة وحتى التمارين المحلولة حتى تتمكن من التدرب على المفهوم وفهمه بالكامل.

كيفية العثور على الموقع النسبي لخطين في الطائرة

معرفة الموضع النسبي بين خطين في الفضاء ثنائي الأبعاد يعتمد على كيفية التعبير عن الخطوط:

• متجهات الاتجاه الخطية: إذا كان هناك خطان لهما متجه اتجاه مختلف، فيجب أن يتقاطعا. من ناحية أخرى، إذا كانت إحداثيات متجهات الاتجاه الخاصة بها متساوية أو متناسبة، فيمكن أن تكون متوازية أو متطابقة (من الضروري التحقق مما إذا كان لديهم نقطة مشتركة).

• المعادلة الصريحة: عندما يكون لخطين ميلين مختلفين

  

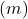
  فإنها تجف، وعلى العكس من ذلك، إذا كانت الخطوط لها نفس الميل ولكن ترتيبها مختلف عند نقطة الأصل

  

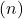
  فهي متوازية. وأخيرًا، يتم الخلط بين الخطين عندما يكون لهما في الأصل منحدرات وإحداثيات متساوية.

• المعادلة العامة (أو الضمنية): الخطان اللذان لهما معاملات غير متناسبة A وB سوف يتقاطعان دائمًا. ومع ذلك، سيكونان متوازيين عندما تكون هاتان المعلمتان متناسبتين مع بعضهما البعض ولكن ليس مع المعامل C. وأخيرًا، عندما تكون الحدود الثلاثة متناسبة، فهذا يعني أن الخطوط ملتبسة.

إذا كان لديك أي شك حول معادلات الخط أعلاه، يمكنك الرجوع إلى شرح معادلات الخط في المستوى . ستجد هنا صيغة جميع المعادلات الخطية، وكيفية حسابها، وأمثلة وتمارين محلولة للمعادلات الخطية.

وفي الجدول التالي لديك ملخص للخصائص السابقة:

بعد ذلك، سنرى مثالين لكيفية تحديد الموضع النسبي بين خطين:

مثال 1

• أوجد الموضع النسبي بين الخطين التاليين المحددين في صورة معادلة صريحة:

الخطان لهما نفس الميل:

لكن لديهم أجهزة كمبيوتر مختلفة في الأصل:

لذا، بما أن لهما نفس الميل ولكن تقاطعاتهما مختلفة، فإن المستقيمين متوازيان .

مثال 2

• حدد الموقع النسبي بين الخطين التاليين معبرًا عنهما بمعادلتهما الضمنية (أو العامة):

يتم التعبير عن كلا الخطين كمعادلة صريحة، لذلك نحن بحاجة لمعرفة ما إذا كان أي من معاملاتهما متناسبة:

الحدود الثلاثة للخطوط متناسبة، وبالتالي فإن الخطوط متطابقة .

تحديد الموقع النسبي لخطين في المستوى باستخدام نظام المعادلات

هناك طريقة أخرى لمعرفة الموضع النسبي بين خطين وهي تحليل نظام المعادلات المتكون من معادلات الخطين:

• إذا كان للنظام حل فريد ، فإن الخطوط تتقاطع. علاوة على ذلك فإن نقطة تقاطع الخطين هي حل النظام.
• أما إذا كان نظاماً بدون حل فهذا يدل على أن الخطوط ليس لها نقاط مشتركة وبالتالي فهي خطوط متوازية.
• إذا كان للنظام عدد لا نهائي من الحلول ، فهذا يعني أن الخطوط تشترك في جميع النقاط، وبالتالي فهي خطوط متقاطعة.

مثال 3

• احسب الموضع النسبي للسطرين التاليين باستخدام نظام المعادلات:

للعثور على الموقع النسبي للخطين، علينا حل نظام المعادلات الخطية التالي الذي يتكون من الخطين:

في هذه الحالة، سوف نقوم بحل النظام بطريقة الاستبدال. لذلك سوف نقوم بعزل المتغير

من المعادلة الثانية ونعوض بها في المعادلة الأولى:

وبمجرد أن نعرف كم يستحق المجهول

نعوض بقيمته في التعبير الموجود لـ

وبذلك حصلنا على حل واحد فقط لمنظومة المعادلات المكونة من الخطين، أي أن الخطين يتقاطعان . ونقطة تقاطعهما هي حل النظام، أي النقطة

حل مسائل الموضع النسبي لخطين في المستوى

التمرين 1

حدد هل المستقيمات التالية متقاطعة أم متوازية أم متطابقة:

يتم التعبير عن كلا الخطين كمعادلة ضمنية (أو عامة)، لذلك نحن بحاجة لمعرفة ما إذا كان أي من معاملاتهما متناسبة:

فقط المعاملان A و B للخطين متناسبان مع بعضهما البعض، وليس مع المعامل C. وبالتالي فإن الخطين متوازيان .

تمرين 2

أوجد الموضع النسبي بين الخطين التاليين معبرا عنه بمعادلات بارامترية:

يمكننا حل نظام المعادلات المكونة من الخطين لإيجاد موضعهما النسبي. ومع ذلك، نظرًا لأنها في شكل معادلات بارامترية، يمكن للمرء بسهولة العثور على متجهات الاتجاه الخاصة بها وإذا لم تكن متناسبة، فهذا يعني أن الخطوط تتقاطع. وفي هذه الحالة، لن نقضي الكثير من الوقت في حل نظام كامل من المعادلات.

بحيث تكون الإحداثيات الديكارتية لمتجه الاتجاه لكل خط هي الأرقام الموجودة أمام المعلمة

بمجرد أن نعرف متجهات الاتجاه، نتحقق من تناسبها:

متجهات الاتجاه غير متناسبة، وبالتالي فإن الخطوط تتقاطع مع بعضها البعض .

التمرين 3

وضح ما إذا كانت الخطوط التالية متقاطعة أو متوازية أو متطابقة وأوجد أيضًا نقطة التقاطع بينهما (إن أمكن).

يتم تعريف الخطين من خلال معادلتهما الصريحة ولهما ميلان مختلفان:

وبما أن لديهم منحدرات مختلفة، فإن الخطوط تتقاطع .

لذلك، بما أن الخطين متقاطعان، فسيكون لديهما نقطة واحدة مشتركة ولحسابها يجب علينا حل نظام المعادلات المكونة من الخطين:

في هذه الحالة سوف نقوم بحل النظام بطريقة المعادلة لأن كليهما

تم حذفها بالفعل:

وبمجرد أن يكون لدينا المجهول

نستبدل قيمته في أي تعبير عن

لمعرفة كم يستحق:

إذن نقطة تقاطع الخطين هي نتيجة النظام:

التمرين 4

احسب قيمة المجهول

و

بحيث يكون الخطان التاليان متوازيين:

يتم وصف الخطوط في شكل معادلة عامة (أو ضمنية). ولذلك، لكي يكون الخطان متوازيين، يجب أن يكون معاملاهما A وB متناسبين، أي يجب تحقيق المعادلة التالية:

ولذلك يجب علينا حل المعادلة السابقة للحصول على قيمة المجهول

للقيام بذلك، نقوم بضرب الكسور بالعرض:

من ناحية أخرى، لكي تكون الخطوط متوازية، لا يمكن أن تكون حدودها المستقلة متناسبة مع المعاملات الأخرى:

لذلك، كما في السابق، نحل المتباينة عن طريق ضرب الكسور بالعرض:

باختصار، بحيث يكون الخطان متوازيين

يجب أن يكون 2 و

يمكن أن يكون أي عدد حقيقي باستثناء 3.

التمرين 5

أوجد المعادلة الصريحة للمستقيم الموازي للخط

وماذا يحدث عبر هذه النقطة

ليكون مستقيما

بحيث يكون الخط موازيا للخط

كلاهما يجب أن يكون لهما نفس المنحدر. ومنحدر الخط

هو 2:

وبالتالي فإن معادلة الخط الذي نحتاج إلى إيجاده ستكون:

وبمجرد أن نعرف ميل الخط، يمكننا حساب تقاطع y عن طريق استبدال النقطة التي تنتمي إلى الخط في معادلة الخط:

وبالتالي فإن المعادلة الصريحة للخط هي:

إذا وصلت إلى هذا الحد، فهذا يعني أنك قد أتقنت بالفعل المواضع النسبية بين سطرين في الخطة. أحسنت!

لكن الشيء الوحيد الذي يتساءل عنه الكثيرون هو… وما الفائدة من معرفة الموقع النسبي بين الخطين؟

حسنًا، أحد تطبيقات الموضع النسبي بين الخطوط هو التمكن من معرفة المسافة بين خطين، حيث أن حساب المسافة بين خطين يعتمد على موضعهما النسبي:

• إذا تقاطع الخطان أو تطابقا، تكون المسافة صفرًا.
• ومن ناحية أخرى، عندما تكون الخطوط متوازية، يجب تطبيق صيغة محددة. إذا كنت مهتمًا أكثر، يمكنك التحقق من كيفية حساب المسافة بين خطين متوازيين .