المواضع النسبية للخط والمستوى

ستجد في هذه الصفحة المواضع النسبية للخط والمستوى. نشرح لك كيفية حساب الموضع النسبي بين الخط والمستوى (طريقتان)، بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتمارين التي تم حلها خطوة بخطوة.

ما هي المواضع النسبية بين الخط والمستوى؟

قبل النظر إلى جميع المواضع النسبية المحتملة بين الخط والمستوى، من الواضح أننا بحاجة إلى معرفة ما هي الخطوط وما هو المستوى . لذلك، إذا لم يكن لديك هذين المفهومين واضحين تمامًا، فنوصيك بإلقاء نظرة أولاً على الصفحات المرتبطة حيث يتم شرح ذلك بالتفصيل.

وهكذا، في الهندسة التحليلية، هناك ثلاثة مواضع نسبية فقط في الفضاء بين الخط والمستوى:

الخط الموجود في المستوى : عندما يكون الخط موجودًا في المستوى فهذا يعني أن لديهم عددًا لا حصر له من النقاط المشتركة.
المستقيم والمستوى الموازي : يكون المستقيم والمستوى متوازيين عندما لا تكون هناك نقطة مشتركة بينهما.
الخط المتقاطع والمستوى : يتقاطع الخط والمستوى عندما يتقاطع الخط مع المستوى عند نقطة ما. لذلك لديهم شيء واحد مشترك فقط.

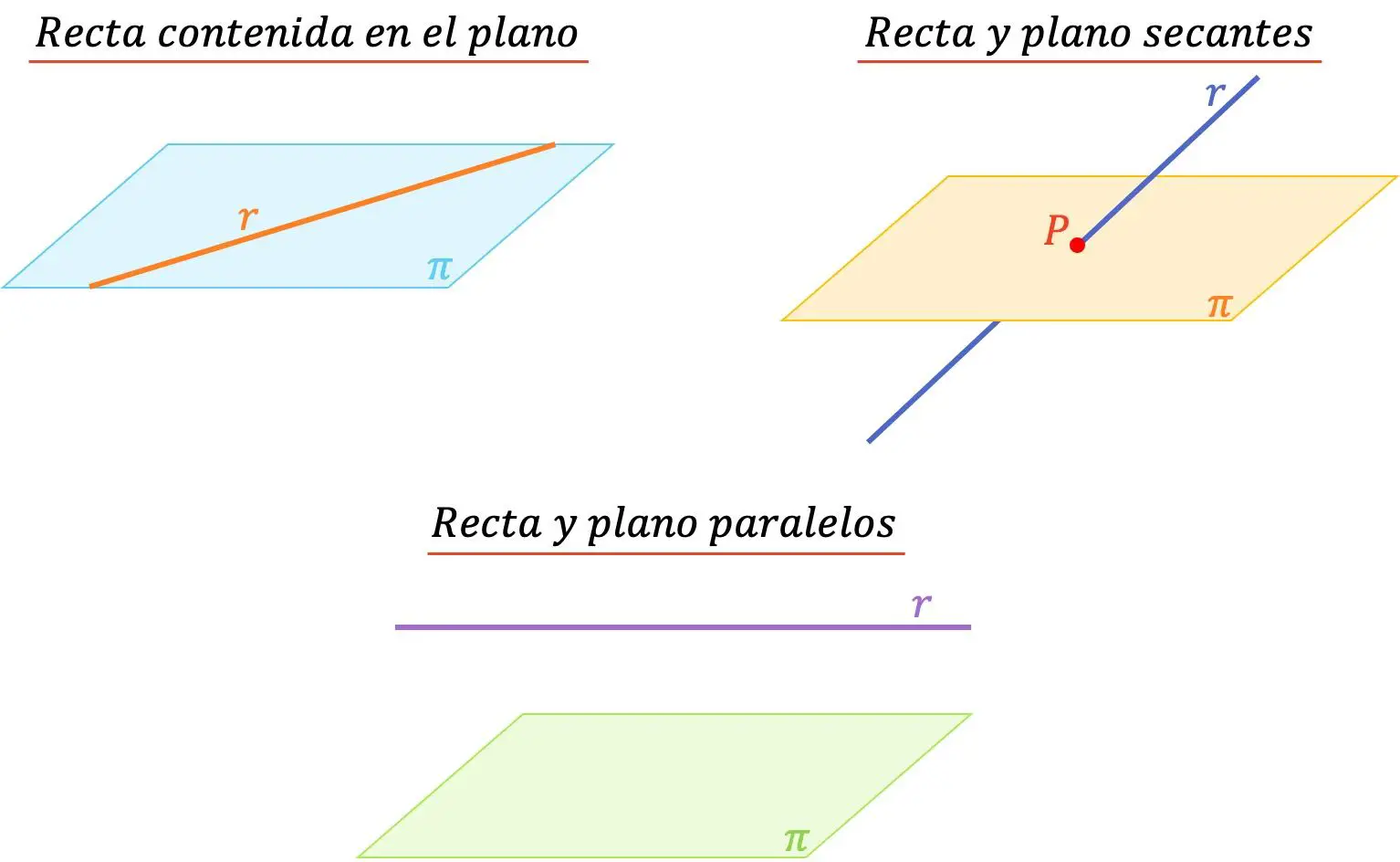
من ناحية أخرى، عندما يكون الخطان موجودين في المستوى أو عندما يكونان موازيين لبعضهما البعض، فإن الزاوية التي يشكلانها ستكون 0 درجة. من ناحية أخرى، عندما يتقاطع الخط والمستوى، يمكن أن تتراوح الزاوية بين العنصرين الهندسيين من 0 درجة (غير مدرجة) إلى 90 درجة (شاملة).

كيفية حساب الموضع النسبي للخط والمستوى؟

هناك طريقتان أساسيتان للعثور على الموضع النسبي بين الخط والمستوى في الفضاء: عن طريق النطاقات أو عن طريق المتجهات .

عندما يتم التعبير عن الخط كمعادلة ضمنية (أو عامة)، فمن الأسهل استخدام طريقة الترتيب. من ناحية أخرى، إذا تم إعطاء الخط مع نوع آخر من المعادلات، على سبيل المثال عندما يكون على شكل متجه أو معادلة بارامترية أو مستمرة، فمن الأسرع استخدام الطريقة المتجهة.

إذا كنت لا تتذكر كيف تبدو معادلات الخط، نترك لك صفحة حيث يمكنك الاطلاع على جميع معادلات الخط . ستجد هنا جميع معادلات الخط، صيغة للعثور بسرعة على معادلة الخط الذي يمر بنقطتين، وأمثلة وتمارين تم حلها خطوة بخطوة.

لذلك، من العملي أكثر استخدام طريقة أو أخرى حسب المشكلة، ولهذا السبب ننصحك بمعرفة كيفية القيام بكلا الإجراءين. وفيما يلي شرح لكلا الطريقتين مع الأمثلة.

عندما يكون الخط على شكل معادلة ضمنية (أو عامة).

إحدى الطرق لتحديد الموضع النسبي بين الخط والمستوى هي حساب رتبة مصفوفتين.

إذا تم تعريف الخط بمعادلاته الضمنية (أو العامة):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}$

ويتم التعبير عن الخطة أيضًا في شكل معادلة عامة:

$\pi : \ A_3x+B_3y+C_3z+D_3=0$

سنسمي A المصفوفة المكونة من المعاملات A وB وC لمعادلات المستوى والخط:

$\displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}$

وستكون المصفوفة A’ هي المصفوفة الموسعة بجميع معاملات المعادلتين:

$\displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}$

ثم يتم تحديد الموقع النسبي بين الخط والمستوى بقيمة مدى المصفوفتين السابقتين حسب الجدول التالي:

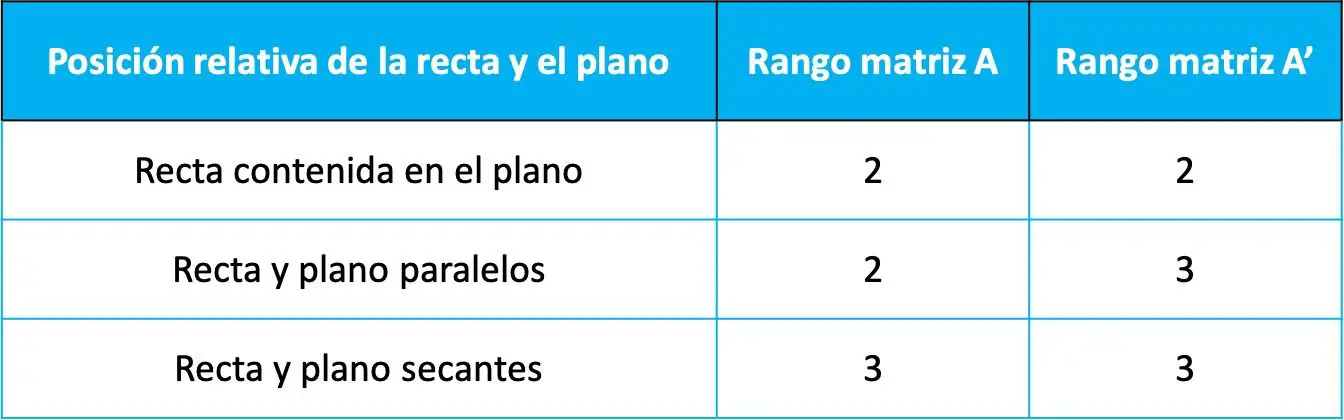
دراسة الموقع النسبي بين الخط والمستوى في الفضاء حسب النطاقات

يمكن إثبات أن المواضع النسبية تعتمد على صفوف هاتين المصفوفتين من نظرية روش-فروبينيوس (نظرية تستخدم لحل أنظمة المعادلات الخطية). ومع ذلك، في هذه الصفحة لن نقوم بالتوضيح لأنه ليس من الضروري معرفتها كما أنها لا تقدم الكثير أيضًا.

مثال لكيفية العثور على الموضع النسبي للخط والمستوى حسب النطاقات

لكي تتمكن من رؤية كيفية القيام بذلك بالضبط، سنحل تمرينًا كمثال:

ادرس الموقع النسبي بين السطر التالي والمستوى التالي:

$\displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}$

$\pi : \ 2x+2y-6=0$

يتم تعريف الخط بمستويين متقاطعين، أي يتم التعبير عنه كمعادلة ضمنية. ولذلك، سوف نستخدم طريقة الرتبة لدراسة الموقع النسبي بين الخط والمستوى.

أول ما يجب فعله هو إنشاء المصفوفة A والمصفوفة الموسعة A’ بمعاملات المعادلات:

$\displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}$

والآن علينا حساب رتبة كل مصفوفة. نوجد أولاً مدى المصفوفة A بالمحددات:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0$

$rg(A) = 2$

محدد المصفوفة A هو صفر ولكنها تحتوي على مصفوفة فرعية 2×2 محددها مختلف عن الصفر، لذا فهي مصفوفة من الرتبة 2.

ومن ناحية أخرى، من الضروري أيضًا حساب رتبة المصفوفة A’. وسيكون مدى المصفوفة الموسعة A’ دائمًا على الأقل نفس نطاق المصفوفة A، لذلك نحتاج فقط إلى التحقق مما إذا كانت من الرتبة 3 أو 2:

$rg(A') = \ ?$

$\displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0$

$rg(A') = 3$

من ناحية أخرى، فإن المصفوفة الموسعة A’ لها محدد فرعي 3×3 مختلف عن 0، وبالتالي فهي في المرتبة 3.

لذا، بما أن المصفوفة A من الرتبة 2 والمصفوفة A’ من الرتبة 3، فإن الخط والمستوى متوازيان .

عندما يكون الخط على شكل نوع آخر من المعادلات

عندما يتم التعبير عن الخط بمعادلة غير المعادلة الضمنية، سواء كانت معادلة متجهة أو بارامترية أو مستمرة، يفضل استخدام الطريقة التي نوضحها أدناه.

لذا، إذا تم إعطاء الخط في صورة معادلة متجهة، أو معادلات بارامترية، أو معادلة متصلة، فهذا يعني أننا نعرف نقطة تنتمي إلى الخط، وأيضًا متجه اتجاهه.

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}$

من ناحية أخرى، نحن نعرف أيضًا ما هو المتجه العمودي (أو المتعامد) على المستوى:

$\vv{n} \perp \pi$

بعد ذلك، من المتجهين ونقطة الخط، يمكن حساب الموضع النسبي بين الخط والمستوى على النحو التالي:

إذا كان المنتج العددي بين متجه الاتجاه للخط والمتجه العمودي للمستوى مختلفًا عن الصفر، فهذا يعني أن الخط قاطع للمستوى.

$\vv{\text{v}}_r\cdot \vv{n} \neq 0 \ \color{orange}\longrightarrow \color{black} \ \text{recta y plano secantes}$
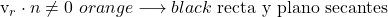
لكن إذا كان حاصل الضرب القياسي بين متجه الاتجاه للخط والمتجه العمودي للمستوى يساوي صفرًا، فهناك احتمالان: الخط موجود في المستوى أو أنهما متوازيان. ولمعرفة هذه الحالة، علينا التعويض بإحداثيات نقطة على الخط في معادلة المستوى.
- إذا كانت النقطة تحقق معادلة المستوى، فإن الخط موجود في المستوى.
- ومن ناحية أخرى، إذا كانت النقطة لا تحقق معادلة المستوى، فإن الخط والمستوى متوازيان.

مثال على تحديد الموضع النسبي للخط والمستوى باستخدام المتجهات

بعد أن رأينا نظرية هذه الطريقة، دعونا نرى الآن تمرينًا تم حله خطوة بخطوة:

أوجد الموضع النسبي بين السطر التالي والمستوى التالي:

$\displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}$

$\pi : \ 2x+y-2z-3=0$

أولاً، يتم تعريف الخط على أنه معادلات بارامترية، لذا فإن متجه اتجاهه والنقطة التي يمر عبرها هما:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}$

ومن ناحية أخرى، فإن المتجه العمودي للمستوى هو:

$\vv{n} =(2,1,-2)$

بمجرد أن نعرف متجه الاتجاه للخط والمتجه العمودي للمستوى، يجب علينا حساب حاصل الضرب القياسي بين الاثنين:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}$

نتيجة الضرب النقطي هي صفر، لذلك لا يمكن احتواء الخط إلا في المستوى أو أن يكون موازيًا له. لذا، لمعرفة هذه الحالة، نعوض بالإحداثيات الديكارتية للنقطة الواقعة على الخط في معادلة المستوى:

$2x+y-2z-3=0 \ \xrightarrow{P(2,-1,0)} \ 2\cdot 2 -1 -2 \cdot 0 -3 = 0$

$4- 1 -0 -3 = 0$

$0 = 0$

من خلال استبدال نقطة الخط في معادلة المستوى نحصل على المساواة، وبالتالي فإن النقطة تحترم معادلة المستوى، وبالتالي، يقع الخط في المستوى .