المقاطع المخروطية - الماثوريتي

ستجد في هذه الصفحة تعريف المقاطع المخروطية، وسبب أهميتها، والأنواع المختلفة للمقاطع المخروطية الموجودة (الدائرة، والقطع الناقص، والقطع الزائد، والقطع المكافئ). بالإضافة إلى ذلك، سوف تكون قادرا على رؤية الاختلافات بين معادلاتها.

ما هي المقاطع المخروطية؟

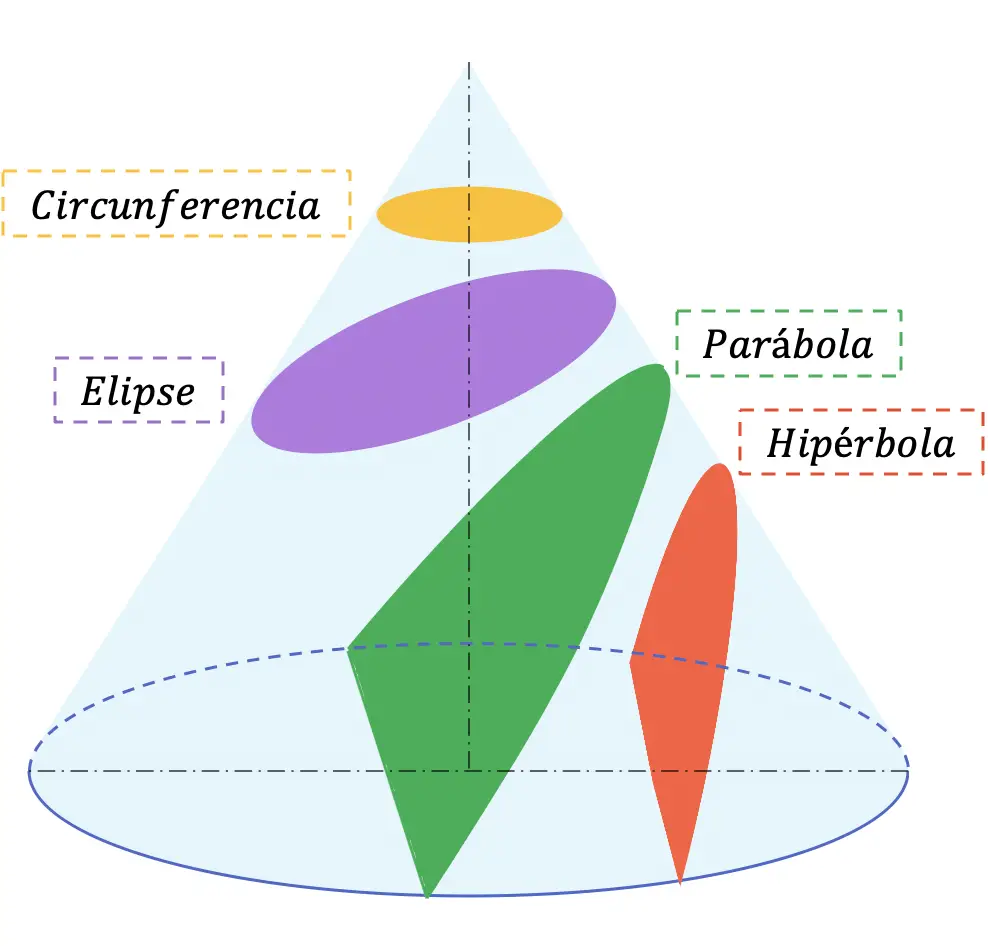
في الهندسة التحليلية، المقاطع المخروطية (أو ببساطة المخروطية) هي جميع المنحنيات الناتجة عن التقاطعات المختلفة بين المخروط والمستوى، عندما لا يمر هذا المستوى عبر قمة المخروط. هناك أربعة أنواع من المقاطع المخروطية: الدائرة، والقطع الناقص، والقطع المكافئ، والقطع الزائد.

فيما يلي الأقسام الأربعة المحتملة التي يمكن الحصول عليها من أي مخروط:

تتم دراسة المقاطع المخروطية بشكل عام في المدرسة الثانوية (Bachillerato) في مادتي الرياضيات والرسم الفني.

أنواع المقاطع المخروطية

بمجرد أن رأينا مفهوم القطع المخروطي، دعونا نرى ما هي الأنواع الأربعة من المقاطع المخروطية الموجودة: الدائرة، والقطع الناقص، والقطع المكافئ، والقطع الزائد.

محيط

المحيط عبارة عن مقطع مخروطي يمكن العثور عليه عن طريق قطع مخروط بمستوى عمودي على محور دورانه (موازي للقاعدة).

بالإضافة إلى ذلك، فإن المحيط هو موضع النقاط على المستوى المتساوي البعد عن نقطة ثابتة تسمى المركز.

الشكل البيضاوي

الشكل البيضاوي عبارة عن خط مسطح ومغلق ومنحني يشبه إلى حد كبير المحيط، لكن شكله أكثر بيضاوية. وينتج على وجه الخصوص عن قطع سطح مخروط بسطح مائل تكون زاويته بالنسبة لمحور الدوران أكبر من زاوية المولد.

بالإضافة إلى ذلك، فإن جميع نقاط الشكل الناقص تحقق شرطًا: القطع الناقص هو المحل الهندسي لجميع نقاط المستوى الذي يكون مجموع المسافات إلى نقطتين ثابتتين أخريين (تسمى البؤرتان F وF’) ثابتًا.

موعظة

في الرياضيات، القطع المكافئ هو موضع النقاط على المستوى التي تكون متساوية البعد عن نقطة ثابتة (تسمى البؤرة) وخط ثابت (يسمى الدليل).

هندسيًا، القطع المكافئ هو نتيجة مقطع مخروط من مستوى بزاوية ميل بالنسبة إلى محور الدوران المكافئة لزاوية المولد للمخروط. ولذلك، فإن المستوى الذي يحتوي على القطع المكافئ يكون موازيًا لمولد المخروط.

من الخصائص المهمة جدًا لهذا المقطع المخروطي معادلة القطع المكافئ ، لأنه اعتمادًا على حالته يسمح لنا بتحديد نوع القطع المكافئ. ستجد في هذا الرابط جميع معادلات القطع المكافئ، ما هي عناصر القطع المكافئ، خواصها، أمثلة، تمارين محلولة،… وغيرها من خصائص القطع المكافئ.

القطع الزائد

كمقطع مخروطي، يتم الحصول على القطع الزائد عندما يتم قطع مخروط بواسطة مستوى بزاوية أقل من الزاوية التي شكلها مولد المخروط بالنسبة إلى محور دورانه.

رياضيًا، يمكن تعريف القطع الزائد على أنه موضع النقاط على المستوى الذي يحقق الخاصية التالية: القيمة المطلقة للفرق في المسافات بين أي نقطة على القطع الزائد ونقطتين ثابتتين (تسمى البؤر) يجب أن تكون ثابتة.

علاوة على ذلك، فإن قيمة طرح هاتين المسافتين تعادل دائمًا المسافة بين رأسي القطع الزائد.

$\lvert d_1 - d_2 \rvert = 2a$

وأنا متأكد من أنك استنتجت بالفعل قيمة المعلمة

$a$

القطع الزائد أمر أساسي للقطع الزائد. في الرابط التالي، يمكنك الاطلاع على شرحنا للقطع الزائد، حيث ستجد سبب أهميته كمعامل بالإضافة إلى جميع العناصر التي تميز القطع الزائد. بالإضافة إلى ذلك، ستجد كيف تبدو معادلة القطع الزائد ، والأنواع المختلفة من القطع الزائد الموجودة، وحتى المسائل والتمارين خطوة بخطوة على القطع الزائد.

المعادلة العامة للقطاعات المخروطية

يمكن التعبير عن كل مقطع مخروطي تحليليا كمعادلة. في الواقع، جميع المعادلات المخروطية يجب أن تكون من الدرجة الثانية:

$Ax^2+Bxy+Cy^2+Dx+Ey+F = 0$

وبالتالي، واحد على الأقل من المعاملات

$A, B$

أيضاً

$C$

يجب أن تكون الصيغة غير صفر.

وبالتالي، اعتمادًا على قيم المعلمات، ستتوافق المعادلة مع نوع واحد من المخروط أو آخر:

المحيط : للمعادلة العامة التي تصف المحيط، المصطلحات
$A$

و

$C$

يجب أن تتطابق و

$B$

يجب أن يكون صفراً.

$A=C \qquad B=0$

القطع الناقص : ستتوافق المعادلة مع التعبير الرياضي للقطع الناقص عند التحقق من الشرط التالي:

$B^2-4AC <0$

القطع المكافئ : لكي تكون المعادلة قطع مكافئ يجب تحقيق المساواة التالية:

$B^2-4AC=0$

القطع الزائد : أخيرًا، يجب أن تحقق المعادلة العامة للقطع الزائد المتباينة التالية:

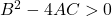$B^2-4AC>0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”112″ style=”vertical-align: -2px;”></p></p> </div> </div> </article> <nav class=$ تصفّح المقالات

→ المقالة السابقة

المقالة التالية ←