المصفوفة الهرمسية (أو الهرميتية)

في هذه الصفحة يمكنك التعرف على ماهية المصفوفة الهرمسية، والمعروفة أيضًا باسم المصفوفة الهرمسية. ستجد أمثلة على المصفوفات الهرمسية، وجميع خصائصها والشكل الذي تتخذه هذه الأنواع من المصفوفات حتى تتمكن من فهمها تمامًا. وأخيرًا، نوضح أيضًا كيفية تحليل أي مصفوفة معقدة إلى مجموع المصفوفة الهرمسية بالإضافة إلى المصفوفة المضادة للهرميتية.

ما هي المصفوفة الهرمسية أو الهرمسية؟

المصفوفة الهرمسية ، أو تسمى أيضًا المصفوفة الهرمسية، هي مصفوفة مربعة ذات أعداد مركبة تتميز بكونها تساوي منقولها المترافق .

$A=A^*$

ذهب

$A^*$

هي مصفوفة تبديل المترافقة

$A$

من باب الفضول، تم تسمية هذا النوع من المصفوفات على اسم تشارلز هيرميت، عالم الرياضيات الفرنسي في القرن التاسع عشر الذي قام بأبحاث مهمة في الرياضيات، وخاصة في مجال الجبر الخطي.

سبب تسمية هذه المصفوفة بهذه الطريقة هو أنها أظهرت أن القيم الذاتية (أو القيم الذاتية) لهذه المصفوفات المعينة هي دائمًا أرقام حقيقية، لكننا سنشرح ذلك بمزيد من التفصيل في خصائص المصفوفات الهرمسية.

أخيرًا، يمكن أيضًا الإشارة إلى هذه المصفوفة أحيانًا على أنها مصفوفة متجاورة ذاتيًا، على الرغم من أن هذا نادر جدًا.

أمثلة على المصفوفات الهرمسية

بمجرد أن رأينا تعريف المصفوفة الهرمسية (أو المصفوفة الهرمسية)، دعونا نرى بعض الأمثلة على المصفوفات الهرمسية ذات الأبعاد المختلفة:

مثال لمصفوفة هيرميتية من الرتبة 2×2

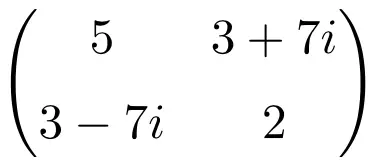
مصفوفة هيرميتية أو هيرميتية ذات أبعاد 2x2

مثال لمصفوفة هيرميتية ذات البعد 3 × 3

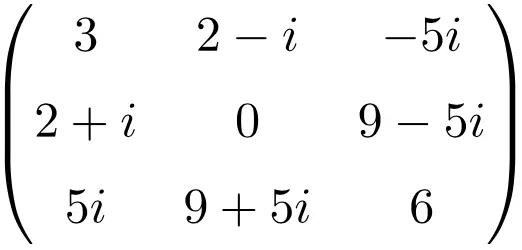
مصفوفة هيرميتية أو هيرميتية ذات أبعاد 3x3

مثال لمصفوفة هيرميتية بحجم 4×4

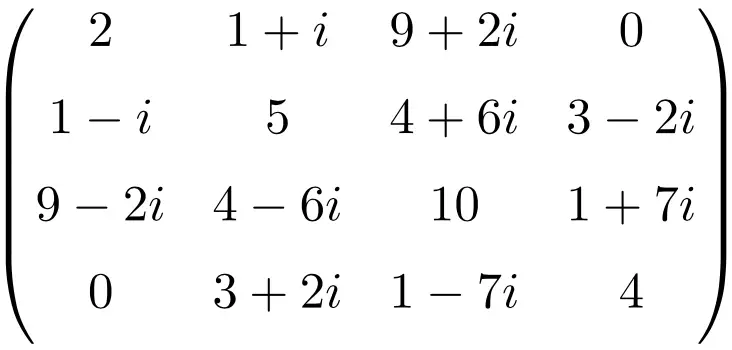
مصفوفة هيرميتية أو هيرميتية ذات أبعاد 4x4

كل هذه المصفوفات هي هرميتية لأن مصفوفة التبديل المترافقة لكل منها تساوي المصفوفة نفسها.

هيكل المصفوفة الهرمسية

تتمتع المصفوفات الهرمسية ببنية سهلة التذكر: فهي مكونة من أرقام حقيقية على القطر الرئيسي، والعنصر المركب الموجود في الصف i والعمود j يجب أن يكون مرافقًا للعنصر الموجود في الصف j -th و العمود التاسع.

فيما يلي بعض الأمثلة على هياكل المصفوفة الهرمسية.

هيكل هيرميتيان 2×2

$\displaystyle \begin{pmatrix}a& b\\[1.1ex] \overline{b} & c \end{pmatrix}$

هيكل هيرميتيان 3×3

$\displaystyle \begin{pmatrix}a& b & c \\[1.1ex] \overline{b} & d & e \\[1.1ex] \overline{c} & \overline{e} & f\end{pmatrix}$

هيكل هرميت 4×4

$\displaystyle \begin{pmatrix}a& b & c & d \\[1.1ex] \overline{b} & e & f & g \\[1.1ex] \overline{c} & \overline{f} & h & i \\[1.1ex] \overline{d} & \overline{g} & \overline{i} & j \end{pmatrix}$

خصائص المصفوفة الهرمسية

وسنرى الآن ما هي خصائص هذا النوع من المصفوفات المركبة المربعة:

أي مصفوفة هيرميتية هي مصفوفة عادية . على الرغم من أنه ليست كل المصفوفات العادية هي مصفوفات هيرميتية.

أي مصفوفة هيرميتية قابلة للقطر. علاوة على ذلك، تحتوي المصفوفة القطرية الناتجة على عناصر حقيقية فقط.

لذلك، فإن القيم الذاتية (أو القيم الذاتية) للمصفوفة الهرمسية هي دائمًا أعداد حقيقية. تم اكتشاف هذه الخاصية من قبل تشارلز هيرميت، ولهذا السبب كان يشرفه أن يطلق على هذه المصفوفة الخاصة جدًا اسم هيرميتيان.

وبالمثل، فإن الفضاءات الذاتية للمصفوفة الهرمسية تكون متعامدة اثنين في اثنين: يوجد أساس متعامد طبيعي لـ
$\mathbb{C}^n$

تتكون من المتجهات الذاتية (المتجهات الذاتية) للمصفوفة.

مصفوفة الأعداد الحقيقية، أي أنه لا يوجد أي عنصر يحتوي على جزء وهمي، تكون هرميتية إذا وفقط إذا كانت مصفوفة متماثلة. مثل على سبيل المثال مصفوفة الهوية 2 × 2 .

يمكن التعبير عن المصفوفة الهرمسية كمجموع مصفوفة متماثلة حقيقية ومصفوفة وهمية غير متماثلة .

$A =B+Ci$

إن مجموع (أو طرح) مصفوفتين هرميتين يساوي مصفوفة هرميتية أخرى، وذلك للأسباب التالية:

$(A\pm B)^* = A^*\pm B^* = A \pm B$

نتيجة ضرب المصفوفة الهرمسية بعددية هي مصفوفة هيرميتية أخرى إذا كان الرقم العددي عددًا حقيقيًا.

$(k \cdot A)^* = \overline{k}\cdot A^* = k \cdot A$

إن منتج مصفوفتين هيرميتيان لم يعد بشكل عام هيرميتيا. ومع ذلك، يكون المنتج هرميًا عندما تكون المصفوفتان قابلتين للتبديل، أي عندما تكون نتيجة ضرب المصفوفتين هي نفسها بغض النظر عن الاتجاه الذي يتم ضربهما فيه، لأنه عندئذ يكون الشرط التالي للعمليات ذات النقل المترافق المصفوفات:

$(A \cdot B)^* = B^*\cdot A^* = B \cdot A = A \cdot B$

إذا كانت المصفوفة الهرمسية قابلة للعكس، فإن معكوسها يتبين أيضًا أنه مصفوفة هيرميتية.

$(A^{-1})^* = (A^*)^{-1} = A^{-1}$

إن محدد المصفوفة الهرمسية يعادل دائمًا عددًا حقيقيًا. وإليكم الدليل على هذه الخاصية:

$det(A) = det(A^t) \ \longrightarrow \ det(A^*) = \overline{det(A)}$

متعطش

$A = A^*$

$det(A) = \overline{det(A)}$

ولذلك، لكي يتحقق هذا الشرط، يجب أن يكون محدد المصفوفة الهرمسية بالضرورة عددًا حقيقيًا. وبهذه الطريقة، فإن مرافق النتيجة يساوي النتيجة نفسها.

تحلل مصفوفة معقدة إلى مصفوفة هيرميتية ومصفوفة مضادة للهرميتية

يمكن أن تتحلل أي مصفوفة تحتوي على عناصر معقدة إلى مجموع مصفوفة هرميتية بالإضافة إلى مصفوفة أخرى مضادة لهرميتية . ولكن لهذا عليك أن تعرف الخصائص التالية لهذه الأنواع من المصفوفات:

مجموع المصفوفة المعقدة المربعة بالإضافة إلى مرافقها المنقول يعطي مصفوفة هرميتية.

$C + C^* = \text{Matriz Hermitiana}$

الفرق بين المصفوفة المعقدة المربعة واقترانها المنقول يعطي مصفوفة مضادة لهرميتي (أو مضادة لهرميتي).

$C - C^* = \text{Matriz Antihermitiana}$

لذلك، يمكن تقسيم جميع المصفوفات المعقدة إلى مجموع مصفوفة هرميتية ومصفوفة مضادة لهرميتية. تُعرف هذه النظرية باسم تحلل تيوبليتز :

$\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}$

حيث C هي المصفوفة المعقدة التي نريد تحللها، C* مرافقتها المنقولة، وأخيرًا A وB هما على التوالي المصفوفات الهرمسية والمضادة للهرميتية التي تتحلل فيها المصفوفة C.

المصفوفة الهرمسية (أو الهرمسية).

ما هي المصفوفة الهرمسية أو الهرمسية؟

أمثلة على المصفوفات الهرمسية

هيكل المصفوفة الهرمسية

خصائص المصفوفة الهرمسية

تحلل مصفوفة معقدة إلى مصفوفة هيرميتية ومصفوفة مضادة للهرميتية

اترك تعليقاً إلغاء الرد