المسافة من نقطة إلى مستوى في الفضاء (الصيغة)

ستجد في هذه الصفحة كيفية حساب المسافة بين النقطة والمستوى في الفضاء (الصيغة). بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتدرب على التمارين التي تم حلها خطوة بخطوة.

ما هي المسافة من نقطة إلى مستوى؟

في الهندسة التحليلية، المسافة من نقطة إلى مستوى هي أقصر مسافة بين النقطة وأي نقطة أخرى على المستوى. هذه المسافة تقابل طول القطعة المتعامدة مع المستوى والتي تمتد من النقطة إلى المستوى.

صيغة المسافة من نقطة إلى مستوى

بعد أن رأينا بالضبط مفهوم المسافة بين نقطة ومستوى، دعونا الآن نرى الصيغة لحساب المسافة المذكورة:

بالنظر إلى نقطة والمعادلة العامة (أو الضمنية) للمستوى:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

صيغة المسافة من نقطة إلى مستوى هي:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

إن إثبات صيغة المسافة من نقطة إلى مستوى ممل وطويل للغاية، لذلك لن نقوم بذلك في هذه الصفحة.

من ناحية أخرى، إذا حصلنا عند تطبيق الصيغة على نتيجة تساوي صفرًا، فهذا يعني بوضوح أن المسافة بين النقطة والمستوى هي صفر، وبالتالي فإن النقطة جزء من ذلك المستوى.

وأخيرا، لاحظ أنه لتطبيق الصيغة، يجب تعريف الخطة كمعادلة عامة (أو ضمنية). لذا، إذا تم التعبير عنها بنوع آخر من المعادلات المستوية، فعلينا أولًا تحويلها إلى معادلة عامة ثم استخدام الصيغة.

مثال لحساب المسافة من نقطة إلى مستوى

ولكي تتمكن من رؤية كيفية تحديد المسافة بين النقطة والمستوى عدديا، سنحل المثال أدناه:

احسب المسافة بين النقطة P والمستوى π. وبعد أن قلت النقطة والخطة:

$P(1,3,-2) \qquad \qquad \pi: \ 2x+5y-4z+7=0$

للعثور على المسافة من النقطة إلى المستوى، ما عليك سوى تطبيق الصيغة الموضحة في القسم أعلاه:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

الآن نعوض بقيمة كل مجهول في الصيغة:

$d(P,\pi) = \cfrac{\lvert 2\cdot 1+5\cdot 3-4\cdot (-2)+7\rvert}{\sqrt{2^2+5^2+(-4)^2}}$

وأخيرًا نقوم بالعمليات:

$d(P,\pi) = \cfrac{\lvert 2+15+8+7\rvert}{\sqrt{4+25+16}}$

$\bm{d(P,\pi) = }\cfrac{\bm{32}}{\bm{\sqrt{45}}}$

لاحظ أنه في بسط الكسر توجد قيمة مطلقة وفي المقام لدينا جذر تربيعي، لذا يجب أن تكون النتيجة موجبة دائمًا. وهذا منطقي لأن المسافات لا يمكن أن تكون سلبية، ولكنها دائما إيجابية.

حساب المسافة بين طائرتين متوازيتين

المستويان المتوازيان يقعان دائمًا على نفس المسافة، لذلك لإيجاد المسافة بين مستويين متوازيين، يمكننا أخذ نقطة على أحد المستويين وحساب المسافة من تلك النقطة إلى المستوى الآخر.

إنها طريقة لإيجاد المسافة بين طائرتين متوازيتين. ومع ذلك، هناك طريقة أبسط للقيام بذلك عندما تتطابق المعاملات A وB وC لمعادلات المستويين:

خذ بعين الاعتبار المعادلات العامة (أو الضمنية) لمستويين متوازيين:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

صيغة حساب المسافة بين مستويين متوازيين هي:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

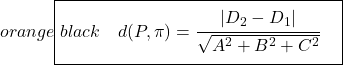
لذا فمن المؤكد أنه من الأسهل العثور على المسافة بين مستويين متوازيين باستخدام الصيغة، لأنها مجرد مسألة تطبيق الصيغة وهذا كل شيء، لكن ذلك يعتمد على المشكلة. بالإضافة إلى ذلك، نعتقد أنه من الأفضل شرح كلتا الطريقتين لحساب المسافة حتى تتمكن من اختيار الطريقة التي تفضلها.

مثال لحساب المسافة بين طائرتين متوازيتين

على سبيل المثال، سوف نحسب المسافة بين المستويين التاليين:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

يجب علينا أولًا أن نتحقق من أننا نتعامل مع طائرتين متوازيتين. وبالتالي، فإن جميع معاملات المعادلات المستوية متناسبة باستثناء الحدود المستقلة، لذا فهما مستويان متوازيان فعليًا.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

وفي هذه الحالة لا تتطابق مصطلحات A وB وC لمعادلات المستويين، لكن يمكننا تحقيق ذلك بقسمة معادلة المستوى الثاني بأكملها على اثنين:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

لذا، فإن معادلات المستويين لها بالفعل نفس المعاملات A وB وC. لذلك، يمكننا بسهولة حساب المسافة بين المستويين باستخدام صيغة المسافة بين مستويين متوازيين:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

نستبدل القيم ونحل العمليات:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

بحيث تكون المسافة بين أحد المستويين والمستوى الآخر تساوي الوحدة.

حل مسائل المسافة من نقطة إلى مستوى

التمرين 1

احسب المسافة بين النقطة P والمستوى الذي تكون معادلته الديكارتية (أو العامة) هي:

$P(2,0,-1) \qquad \qquad \pi: \ x-3y+2z-4=0$

انظر الحل

لحساب المسافة من النقطة إلى المستوى، يجب عليك استخدام الصيغة المقابلة:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

نستبدل قيمة كل معلمة في الصيغة:

$d(P,\pi) = \cfrac{\lvert 1\cdot 2+(-3)\cdot 0+2\cdot (-1)-4\rvert}{\sqrt{1^2+(-3)^2+2^2}}$

وأخيرًا نقوم بالعمليات:

$d(P,\pi) = \cfrac{\lvert 2+0-2-4\rvert}{\sqrt{1+9+4}}$

$d(P,\pi) = \cfrac{\lvert -4\rvert}{\sqrt{14}}$

$\bm{d(P,\pi) = }\cfrac{\bm{4}}{\bm{\sqrt{14}}}$

تمرين 2

أوجد المسافة بين النقطة P والمستوى π:

$P(-1,4,3) \qquad \qquad \pi: \ y=5x-2z$

انظر الحل

قبل استخدام صيغة المسافة من نقطة إلى مستوى، يجب علينا أولاً التعبير عن المستوى في شكل معادلة ضمنية (أو عامة):

$\pi: \ -5x+y+2z=0$

والآن يمكننا استخدام الصيغة لتحديد المسافة من النقطة إلى المستوى:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

نعوض بقيمة كل حد في الصيغة:

$d(P,\pi) = \cfrac{\lvert -5\cdot (-1)+1\cdot 4+2\cdot 3+0\rvert}{\sqrt{(-5)^2+1^2+2^2}}$

وأخيرا نقوم بتنفيذ العمليات:

$d(P,\pi) = \cfrac{\lvert 5+4+6\rvert}{\sqrt{25+1+4}}$

$\bm{d(P,\pi) = }\cfrac{\bm{15}}{\bm{\sqrt{30}}}$

التمرين 3

استخدم صيغة المسافة بين نقطة ومستوى لتحديد ما إذا كانت النقطة P تقع في المستوى π.

$P(0,-3,5) \qquad \qquad \pi: \ 4x+6y+2z+8=0$

انظر الحل

للتحقق مما إذا كانت النقطة تنتمي إلى المستوى، يمكننا حساب المسافة بين الاثنين: إذا كانت المسافة صفرًا فهذا يعني أن النقطة تنتمي إلى المستوى، ومن ناحية أخرى إذا كانت المسافة مختلفة عن 0 فهذا يعني أن النقطة تنتمي إلى المستوى. النقطة خارج الطائرة. يخطط.

لذلك، نحدد المسافة بين النقطة والمستوى من الصيغة:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

$d(P,\pi) = \cfrac{\lvert 4\cdot 0+6\cdot (-3)+2\cdot 5+8\rvert}{\sqrt{4^2+6^2+2^2}}$

$d(P,\pi) = \cfrac{\lvert -18+10+8\rvert}{\sqrt{16+36+4}}$

$d(P,\pi) = \cfrac{0}{\sqrt{56}}$

$\bm{d(P,\pi) = 0}$

المسافة بين النقطة والمستوى تعادل الصفر، وبالتالي فإن النقطة تنتمي فعليًا إلى المستوى.

التمرين 4

أوجد المسافة بين المستويين التاليين:

$\pi_1 : \ 2x-y+5z-3=0 \qquad \qquad \pi_2 : \ 2x-y+5z-7=0$

انظر الحل

يجب علينا أولًا أن نتحقق من أننا نتعامل مع طائرتين متوازيتين. جميع معاملات معادلات المستويين متناسبة باستثناء الحدود المستقلة، فهما مستويان متوازيان بالفعل.

$\cfrac{2}{2}=\cfrac{-1}{-1}=\cfrac{5}{5} \neq \cfrac{-3}{-7} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

في هذه الحالة، سنحسب المسافة بين المستويين بالصيغة، حيث أن معاملاتهم A وB وC متساوية:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

لذلك، نستبدل القيم في الصيغة ونجري العمليات:

$d(P,\pi) = \cfrac{\lvert -7-3\rvert}{\sqrt{2^2+(-1)^2+5^2}}= \cfrac{\lvert -10\rvert}{\sqrt{30}} = \cfrac{\bm{10}}{\bm{\sqrt{30}}}$

التمرين 5

أوجد المسافة بين المستويين المتوازيين التاليين:

$\pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0$

انظر الحل

يتم تعريف المستوى الأمامي في شكل معادلات بارامترية، لذا لتطبيق صيغة المسافة بين مستويين متوازيين علينا أولاً تحويلها إلى شكل معادلة عامة ويستغرق الأمر الكثير من الحسابات والوقت. ومن ثم، فمن الأسرع أن نأخذ نقطة على هذا المستوى ونحسب المسافة من تلك النقطة إلى المستوى الآخر.

وبالتالي، فإن إحداثيات النقطة التي يمر عبرها المستوى π ₁ تتوافق مع الحدود المستقلة لكل معادلة بارامترية:

$P(3,-2,5)$