المسافة من خط إلى مستوى في الفضاء

ستجد هنا كيفية حساب المسافة من الخط إلى المستوى، وبالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتمارين التي تم حلها خطوة بخطوة.

ما هي المسافة بين الخط والطائرة؟

في الهندسة التحليلية، المسافة بين الخط والمستوى في الفضاء تعتمد على الموقع النسبي بين هذين العنصرين الهندسيين:

إذا كان المستقيم داخل المستوى أو كان المستقيم والمستوى متوازيين فإن المسافة التي تفصل بينهما تساوي صفراً.
إذا كان الخط موازيا للمستوى ، يتم إيجاد المسافة من الخط إلى المستوى عن طريق أخذ أي نقطة على الخط وحساب المسافة من تلك النقطة إلى المستوى.

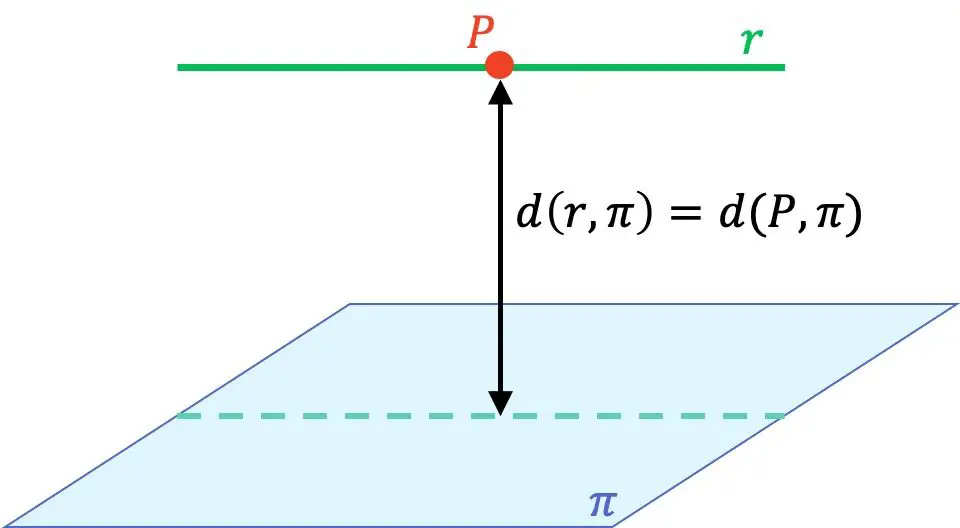
لذلك، لحساب المسافة من خط إلى مستوى، من الضروري أن تعرف كيفية تحديد الموضع النسبي بين الخط والمستوى وكيفية حساب المسافة بين نقطة ومستوى . لذا، إذا لم تكن واضحًا تمامًا أو لا تعرف الصيغ، ننصحك بإلقاء نظرة أولاً على الصفحات المرتبطة، حيث ستجد شروحات وأمثلة وتمارين تم حلها خطوة بخطوة.

مثال لحساب المسافة بين الخط والمستوى

لكي تتمكن من معرفة كيفية إيجاد المسافة بين الخط والمستوى في الفضاء (في R3)، سنحل مسألة كمثال:

كم يبعد الخط
$r$

على متن الطائرة

$\pi$

؟

$\displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}$

$\pi : \ 4x+2y+z-6=0$

للعثور على المسافة بين الخط والمستوى، عليك أولاً معرفة الموضع النسبي بين الاثنين.

فمن ناحية، يتم تعريف الخط على شكل معادلات بارامترية، بحيث يكون متجه اتجاهه والنقطة التي يمر عبرها هما:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}$

ومن ناحية أخرى، فإن المتجه العمودي للمستوى هو:

$\vv{n} =(4,2,1)$

وبالتالي، لتحديد الموضع النسبي بين المستوى والخط، من الضروري حساب المنتج القياسي بين متجه اتجاه الخط والمتجه العمودي للمستوى:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}$

نتيجة الضرب النقطي هي صفر، لذلك لا يمكن احتواء الخط إلا في المستوى أو أن يكون موازيًا له. لذا، لمعرفة هذه الحالة، نعوض بالإحداثيات الديكارتية للنقطة الواقعة على الخط في معادلة المستوى:

$4x+2y+z-6=0 \ \xrightarrow{P(-2,1,-1)} \ 4\cdot (-2) +2\cdot 1 -1-6= 0$

$-8+2-1-6 = 0$

$-13 \neq 0$

وبتعويض نقطة الخط في معادلة المستوى نحصل على عدم مساواة، وبالتالي فإن النقطة لا تحترم معادلة المستوى، وبالتالي يكون الخط والمستوى متوازيين.

بمجرد أن عرفنا أن الخط المستقيم والمستوى متوازيان، يمكننا الآن حساب المسافة الهندسية بينهما. للقيام بذلك، نأخذ النقطة الواقعة على الخط ونحسب المسافة من تلك النقطة إلى المستوى.

$P(-2,1,-1) \qquad \qquad \pi: \ 4x+2y+z-6=0$

لذلك، نستخدم صيغة المسافة من نقطة إلى مستوى:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

الآن نعوض بقيمة كل مجهول في الصيغة:

$d(P,\pi) = \cfrac{\lvert 4\cdot (-2)+2\cdot 1+1\cdot (-1)-6\rvert}{\sqrt{4^2+2^2+1^2}}$

وأخيرا نقوم بتنفيذ العمليات:

$d(P,\pi) = \cfrac{\lvert -8+2-1-6\rvert}{\sqrt{16+4+1}}$

$d(P,\pi) = \cfrac{\lvert -13\rvert}{\sqrt{21}}$

$d(P,\pi) = \cfrac{13}{\sqrt{21}}$

بحيث تكون المسافة بين الخط والمستوى تعادل المسافة بين النقطة والمستوى المحسوبة:

$\bm{d(r,\pi)=d(P,\pi) = }\cfrac{\bm{13}}{\bm{\sqrt{21}}}$

من الواضح أن المسافة يجب أن تعطينا دائمًا قيمة إيجابية، لأن المسافات دائمًا إيجابية. إذا حصلنا على نتيجة سلبية، فهذا يعني أننا ارتكبنا خطأ أثناء اتخاذ خطوة ما.

ما هي المسافة بين الخط والطائرة؟

مثال لحساب المسافة بين الخط والمستوى

اترك تعليقاً إلغاء الرد