المسافة بين نقطة وخط

ستجد هنا الصيغة المستخدمة لحساب المسافة بين نقطة وخط. بالإضافة إلى ذلك، ستتمكن من رؤية العديد من الأمثلة والتدريبات المحلولة للمسافات بين النقاط والخطوط، وحتى التطبيقات التي تتضمنها هذه العملية (على سبيل المثال، إيجاد المسافة بين الخطوط المتوازية).

صيغة المسافة بين النقطة والخط

المسافة بين نقطة وخط هي أقصر مسافة بين تلك النقطة والخط. رياضياً، هذه المسافة الدنيا تعادل طول القطعة المرسومة من النقطة إلى الخط المستقيم والمتعامدة مع الخط.

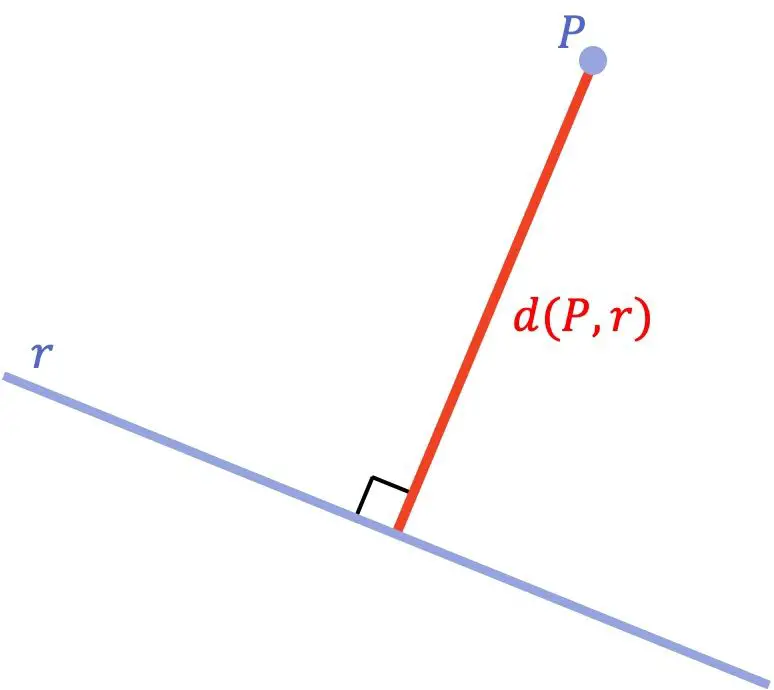
بعد أن رأينا المفهوم الهندسي للمسافة بين نقطة وخط، دعونا نرى ما هي الصيغة المستخدمة لحساب المسافة المذكورة:

بالنظر إلى المعادلة الضمنية (أو العامة) للخط وإحداثيات أي نقطة على المستوى:

$r: \ Ax+By+C=0 \qquad \qquad P(p_x,p_y)$

صيغة المسافة بين النقطة والخط هي:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

هام: لاحظ أن معادلة الخط في الصيغة تكون على شكل معادلة ضمنية (أو عامة)، فإذا كان لدينا الخط المعبر عنه في نوع آخر من المعادلات، نحتاج إلى تمريره أولاً إلى معادلته الضمنية ثم يمكننا تطبيق الصيغة.

مثال لحساب المسافة بين نقطة وخط

يمكنك أدناه رؤية مثال لحساب المسافة بين نقطة وخط:

أوجد المسافة بين النقطة
$P$

والقانون

$r:$

$P(2,-1) \qquad \qquad r: \ 3x+4y-5=0$

لحساب المسافة بين النقطة والخط، ما عليك سوى تطبيق الصيغة:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

والآن نستبدل كل حد بقيمته:

$d(P,r)= \cfrac{\lvert 3\cdot 2 + 4\cdot (-1)-5\rvert}{\sqrt{3^2+4^2}}$

وأخيرا نحسب المسافة:

$d(P,r)= \cfrac{\lvert 6 -4-5\rvert}{\sqrt{9+16}} =\cfrac{\lvert -3 \rvert}{\sqrt{25}} = \mathbf{\cfrac{3}{5}}$

المسافة بين خطين متوازيين

أحد تطبيقات حساب المسافة بين الخط والنقطة هو إيجاد المسافة بين الخطوط المتوازية.

من الواضح أنه لفهم المفهوم الذي سنشرحه أدناه، يجب أن تعرف ما هي الخطوط المتوازية ، فإذا كنت لا تعرف تعريفها بالضبط، نترك لك رابطًا نشرحه فيه بالتفصيل وستتمكن أيضًا من رؤية الأمثلة من الخطوط المتوازية.

للعثور على المسافة بين خطين متوازيين، ما عليك سوى أخذ نقطة على أحد الخطين وحساب المسافة من تلك النقطة إلى الخط الآخر.

لذلك، لتحديد المسافة بين خطين متوازيين، يتم استخدام صيغة المسافة بين الخط والنقطة أيضًا.

من ناحية أخرى، إذا حصلنا عند استخدام الصيغة على مسافة 0 وحدة، فهذا يعني أن الخطوط تلامس بعضها البعض في نقطة ما، وبالتالي فإن الخطوط ليست متوازية، ولكنها متقاطعة أو متطابقة أو متعامدة. إذا أردت، يمكنك التحقق من الاختلافات بين هذا النوع من الخطوط على موقعنا.

لذلك دعونا نرى كيفية حل مشكلة المسافة بين خطين متوازيين من خلال مثال:

أوجد المسافة بين الخطين المتوازيين التاليين:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

أول شيء يتعين علينا القيام به هو الحصول على نقطة على أحد الخطوط (الخط الذي تريده). في هذه الحالة، سوف نقوم بحساب نقطة على الخط

$s.$

للقيام بذلك، يجب عليك إعطاء قيمة لأحد المتغيرات، على سبيل المثال سنفعل

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

والآن نقوم بمسح المتغير الآخر (

$y$

) من المعادلة التي تم الحصول عليها لمعرفة كم قيمتها في هذه المرحلة:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

ولذلك، فإن النقطة التي تم الحصول عليها من الخط

$s$

شرق:

$P(0,-2)$

وبمجرد أن يكون لدينا بالفعل نقطة على الخط، فإننا نحسب المسافة من تلك النقطة إلى الخط الآخر باستخدام الصيغة:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{2}{\sqrt{20}}=\bm{0,45}$

حل مسائل المسافة بين النقطة والخط

التمرين 1

حساب المسافة بين النقطة

$P$

والقانون

$r:$

$P(4,2) \qquad \qquad r: \ 5x-3y+6=0$

انظر الحل

للعثور على المسافة بين نقطة وخط، ما عليك سوى تطبيق الصيغة:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

نستبدل كل حد بقيمته ونحسب المسافة:

$d(P,r)= \cfrac{\lvert 5\cdot 4 + (-3)\cdot 2+6\rvert}{\sqrt{5^2+(-3)^2}}=\cfrac{20}{\sqrt{34}}= \bm{3,43}$

تمرين 2

ما هي المسافة بين النقطة

$P$

والقانون

$r$

$P(-3,-1) \qquad \qquad r: \ y=-3x+5$

انظر الحل

في هذه الحالة، تكون معادلة الخط في الصورة الضمنية (أو العامة). بدلاً من ذلك، لاستخدام صيغة المسافة من نقطة إلى خط، يجب التعبير عن الخط كمعادلة ضمنية. لذلك يجب علينا أولاً تحويل الخط وتمريره إلى معادلة ضمنية (فقط قم بتمرير جميع الحدود على نفس الجانب من المعادلة):

$r: \ 3x+y-5=0$

وبمجرد أن يكون الخط في شكل واضح بالفعل، يمكننا الآن استخدام صيغة المسافة بين النقطة والخط:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

لذلك نعوض كل حد بقيمته ونحسب المسافة:

$d(P,r)= \cfrac{\lvert 3\cdot (-3) + 1\cdot (-1)-5\rvert}{\sqrt{3^2+1^2}}=\cfrac{\lvert -9-1-5\rvert}{\sqrt{9+1}}=\cfrac{15}{\sqrt{10}}= \bm{4,74}$

التمرين 3

ما المسافة بين السطرين التاليين؟

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

انظر الحل

أولاً، سوف نتحقق من أن هذين الخطين متوازيان. لهذا، معاملات المتغيرات

$x$

$y$

يجب أن تكون متناسبة مع بعضها البعض ولكن ليس مع الشروط المستقلة:

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

في الواقع، الخطوط متوازية، وبالتالي يمكننا تطبيق الإجراء.

الآن نحن بحاجة للحصول على نقطة من أحد الخطوط (الخط الذي تريده). في هذه الحالة، سوف نقوم بحساب نقطة على الخط

$s.$

للقيام بذلك، يجب عليك تعيين قيمة لأحد المتغيرات، على سبيل المثال سنفعل

$x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$

والآن نقوم بمسح المتغير الآخر (

$y$

) للمعادلة التي تم الحصول عليها لمعرفة قيمتها عند هذه النقطة:

$6y=-6$

$y= \cfrac{-6}{6}$

$y= -1$

بحيث يتم الحصول على النقطة من السطر

$s$

شرق:

$P(0,-1)$

بمجرد أن نعرف نقطة على الخط، نحسب المسافة من تلك النقطة إلى الخط الآخر بالصيغة:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 1\cdot 0 + 3\cdot (-1) +(-4)\rvert}{\sqrt{1^2+3^2}}= \cfrac{7}{\sqrt{10}}=\bm{2,21}$

التمرين 4

احسب قيمة المجهول

$k$

بحيث المسافة بين النقطة

$P$

والقانون

$r$

أي 5 وحدات.

$P(-2,5) \qquad \qquad r: \ 12x-5y+k=0$

انظر الحل

يجب علينا أولاً تطبيق صيغة المسافة بين النقطة والخط:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

الآن نستبدل كل حد بقيمته ونبسط التعبير:

$d(P,r)= \cfrac{\lvert 12\cdot (-2) + (-5)\cdot 5+k\rvert}{\sqrt{12^2+(-5)^2}}= \cfrac{\lvert -24-25+k\rvert}{\sqrt{169}}=\cfrac{\lvert -49+k\rvert}{13}$