كيفية حساب محدد مصفوفة 2×2

في هذه الصفحة سوف تتعلم ما هو محدد مصفوفة 2 × 2. بالإضافة إلى ذلك، ستجد أمثلة وتمارين تم حلها خطوة بخطوة حول كيفية حل محددات الترتيب 2، حتى تتمكن من التدرب عليها وفهمها بشكل مثالي.

ما هو المحدد 2×2؟

محدد الرتبة 2 هو مصفوفة البعد 2 × 2 ممثلة بشريط رأسي على كل جانب من المصفوفة. على سبيل المثال، إذا كان لدينا المصفوفة التالية:

\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}

يتم تمثيل محدد المصفوفة A على النحو التالي:

\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}

كما رأيت، فإن كتابة محدد مصفوفة مربعة 2×2 أمر سهل. الآن دعونا نرى كيف يتم حسابه:

كيفية حل محدد الطلب 2؟

لحساب محدد مصفوفة 2×2، نحتاج إلى ضرب عناصر القطر الرئيسي وطرح حاصل ضرب القطر الثانوي.

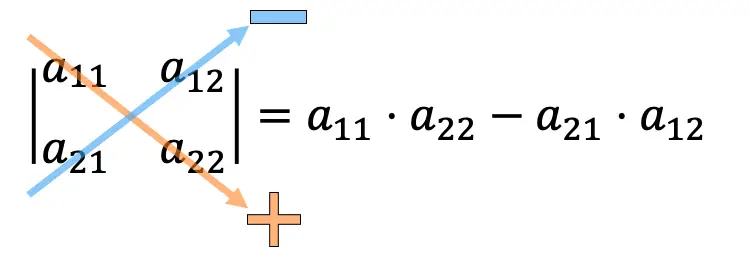
مثال لحساب محدد مصفوفة 2x2

أمثلة لحساب المحددات 2×2:

\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}

\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}

حل مسائل محددات المصفوفات 2 × 2

التمرين 1

احسب المحدد 2×2 التالي:

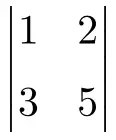
حل التمرين خطوة بخطوة للمحدد 2x2

لإنشاء محدد 2×2، يجب عليك ضرب عناصر القطر الرئيسي وطرح حاصل ضرب القطر الثانوي:

\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}

تمرين 2

حل محدد البعد 2×2 التالي:

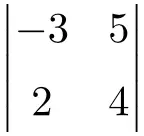
تمارين تم حلها خطوة بخطوة لمحددات 2x2

لإيجاد حل محدد الدرجة 2، عليك ضرب عناصر القطر الرئيسي وطرح حاصل ضرب القطر الثانوي:

\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}

التمرين 3

أوجد حل محدد الترتيب 2 التالي:

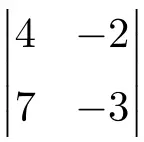
تمرين تم حله خطوة بخطوة لمحدد مصفوفة 2×2

لإيجاد حل محدد البعد 2، عليك ضرب عناصر القطر الرئيسي وطرح حاصل ضرب القطر الثانوي:

\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}

التمرين 4

احسب المحدد 2×2 التالي:

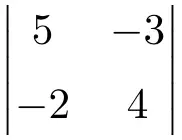
كيفية حل محدد مصفوفة 2×2، تمرين تم حله خطوة بخطوة

لحساب محددات المصفوفات 2×2، نحتاج إلى ضرب عناصر القطر الرئيسي وطرح حاصل ضرب القطر الثانوي:

\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}

التمرين 5

أوجد نتيجة المحدد 2×2 التالي:

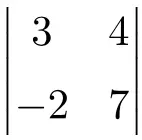
تم حل التمرين على الحل خطوة بخطوة لمحدد مصفوفة من الرتبة 2

لإيجاد حل للمحدد 2×2، نحتاج إلى ضرب عناصر القطر الرئيسي وطرح حاصل ضرب القطر الثانوي:

\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}

ساطع! أنت تعرف الآن كيفية إنشاء محددات البعد 2×2! أنت الآن بالتأكيد قادر على فهم كيفية حساب المحدد 3×3 وأيضًا كيفية حل محدد المصفوفة 4×4 .

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top