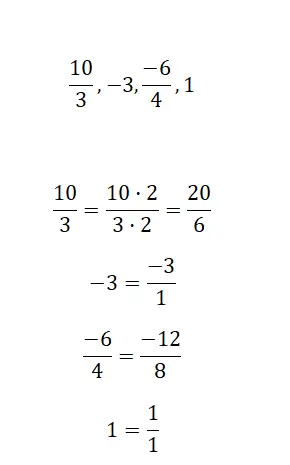ستجد في هذه المقالة شرحًا كاملاً وسهل الفهم حول الكسور المتكافئة أو الكسور المتساوية . وبشكل أكثر تحديدًا، سنتحدث عن تعريفهما وكيفية حسابهما وكيفية معرفة ما إذا كان الكسران متكافئين أم لا. بهذه الطريقة ستنتهي بمعرفة كل ما تحتاجه لحل التمارين على الكسور المتكافئة مثل تلك التي سنقدمها لك في النهاية. ومع ذلك، لنبدأ بالموضوع.
حاسبة الكسور المكافئة
بمساعدة حاسبة الكسور المتكافئة، ستتمكن من التحقق مما إذا كان الكسران متساويان، دون الحاجة إلى إجراء أي حسابات. عملها بسيط للغاية، حيث يتعين عليك في الأساس إدخال القيم المقابلة للبسطين والمقامين والضغط على زر “احسب”.
ما هي الكسور المتكافئة؟
الكسور المتكافئة هي تلك التي تعبر عن نفس القيمة العددية ، وبالتالي فهي كسور مكافئة لنفس النتيجة، حتى لو كان لها بسط ومقام مختلفان. وهذا يعني أن بينهما علاقة تناسب، والتي يمكن أن تكون من نوعين: مكبرة أو مبسطة. بعد ذلك، نعرض لك مثالًا بيانيًا للكسور المتكافئة حتى يتم فهم المفهوم بشكل أفضل.
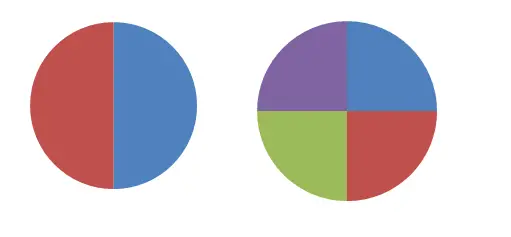
في الصورة السابقة يمكنك رؤية دائرتين مقسمتين إلى قسمين وأربعة أجزاء. إذا حاولنا تعريف الأول بالكسر، فسنقول أن كل جزء يساوي 1/2 من الكل، بينما في الشكل الثاني سنستخدم الكسر 1/4. من الواضح أن هذين الكسرين ليسا متكافئين ، لأنهما يمثلان كميات مختلفة. لكن إذا أخذنا قطعتين من الدائرة الثانية (2/4)، فإن هذا التعبير يعادل 1/2.
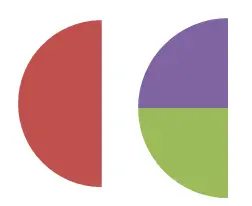
وفي هذه الصورة الثانية يمكنك رؤية التكافؤ بين 1/2 و 2/4 كما يمكن التحقق منه عدديا. بما أن 1/2 = 0.5 و2/4 = 0.5. ووفقا للتعريف الذي علقنا عليه سابقا، إذا كان الكسران يعبران عن نفس القيمة العددية، فإنهما كسران متكافئان.
أمثلة على الكسور المتكافئة
سنعرض لك الآن 5 أمثلة للكسور المتكافئة. وإذا كنت تريد أن تفهم كيف قمنا بحسابها، فنوصيك بمواصلة القراءة.
- الكسور المكافئة للنصف: 2/4، 3/6، 4/8، إلخ.
- كسور تعادل الثلث: 2/6، 3/9، 4/12، إلخ.
- الكسور المكافئة للربع: 2/8، 3/12، 4/16، إلخ.
- الكسور المساوية للوحدة: 4/4، 7/7، 15/15، إلخ.
- كسور تعادل الخمس: 2/10، 3/15، 4/20، إلخ.
كيفية حساب الكسور المتكافئة؟
للحصول على كسور متكافئة، علينا ضرب البسط والمقام أو قسمتهما على نفس العدد. لأنه إذا عدلنا جزأي الكسر بنفس الطريقة، فسنحافظ على علاقة تناسب. لذلك يمكننا استخدام طريقتين: التضخيم والتصغير.
العثور على كسر مكافئ عن طريق التضخيم
في هذه الحالة الأولى، علينا ضرب الكسر الأولي في قيمة عددية معينة. هذا يعني أن علينا ضرب البسط والمقام في هذا العدد. ولكي تتمكن من رؤية ذلك بمثال، نعرض لك أدناه كسرين متكافئين، يتم الحصول عليهما بعد إجراء الضرب:
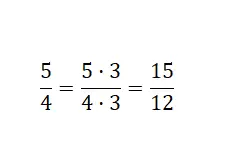
ما فعلناه هو ضرب كلا جزأين الكسر في ثلاثة: 5 x 3 = 15 و 4 x 3 = 12 . وبذلك نحصل على جزء مكافئ مضخم، لأنه أكبر. وفي الختام وجدنا كسرا مكونا من قيم عددية مختلفة، يعبر عن نفس كمية الكسر الأصلي.
إيجاد الكسر المكافئ بالتبسيط
ثانيًا، يمكننا اختيار تبسيط الكسر عن طريق قسمة البسط والمقام لكسر معين. بهذه الطريقة سنحصل على كسر مكافئ آخر ، حتى أبسط من الأول. ومع ذلك، تجدر الإشارة إلى أن هذه الطريقة لا تعمل إلا إذا كان التعبير الأولي ليس كسرًا غير قابل للاختزال ، حيث لا يمكن اختزال هذا الأخير أكثر. فيما يلي مثال لحساب الكسر المكافئ عن طريق التخفيض (التبسيط).
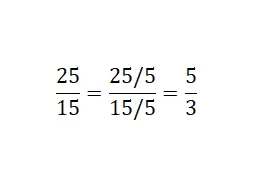
كما ترون في الصورة، ما فعلناه هو قسمة كل من بسط الكسر ومقامه على قاسم مشترك . في هذا المثال، استخدمنا خمسة: 25/5 = 5 و15/5 = 3. وأخيرًا، حصلنا على الكسر المكافئ غير القابل للاختزال وهو 25/15.
كيف يمكنك معرفة ما إذا كان الكسران متكافئين؟
لتحديد الكسور المتكافئة، يجب علينا اتباع أحد الإجراءات الثلاثة التي سنشرحها أدناه. وتجدر الإشارة إلى أن الثاني يتعلق بتبسيط الكسور التي تحدثنا عنها في القسم السابق.
ضرب البسط بالمقامات
إذا كنت تريد التحقق من التكافؤ بين كسرين، يمكنك استخدام هذا الإجراء الأول. في الأساس، عليك ضرب بسط الكسر الأول في مقام الثاني. بعد ذلك، عليك أن تضرب بسط الكسر الثاني في مقام الكسر الأول. إذا كانت كلتا النتيجتين تعطيك نفس النتيجة، فإن هذه الكسور ستكون متكافئة. ننظر إلى المثال التالي:
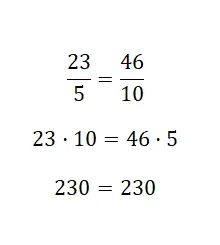
في هذا المثال الأخير، تحققنا من أن الكسرين متساويان. كان من السهل رؤية هذا المثال، حيث أن الكسر الثاني هو ضعف الأول، أي أن لديهم علاقة تكافؤ مضخمة . تجدر الإشارة إلى أن هذا الإجراء مريح للغاية للاستخدام، وهو ما يكفي فقط لضرب الصلبان. لكننا ننصحك أيضًا بتعلم كيفية استخدام النظامين الآخرين، لأن هذا سيمنحك المزيد من الموارد الرياضية المتاحة لك.
تبسيط الكسور
عندما يتعلق الأمر بالكسور غير القابلة للاختزال ، يمكننا استخدام هذه الطريقة الأخرى التي تتمثل في تقليل الكسر المكون من أكبر الأعداد قدر الإمكان. إذا وجدنا، عند إجراء هذا التخفيض، أن الكسر الأصغر هو الجزء غير القابل للاختزال من الآخر، فيمكننا أن نفترض أنهما متساويان.
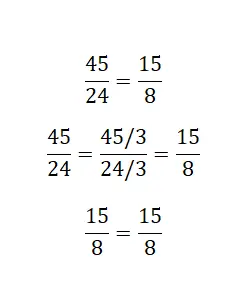
حل ومساواة الانقسامات
وأخيرًا، يمكنك اللجوء إلى حل خارج القسمة الناتج عن الكسور، لأن العدد الكسري دائمًا ما يكون قسمة. في الأساس، تحتاج إلى حساب القيمة العددية المكافئة للكسرين، وإذا كان نفس الرقم، فسيكونان متساويين. وفي الصورة التالية يمكنك رؤية مثال واضح جدًا:
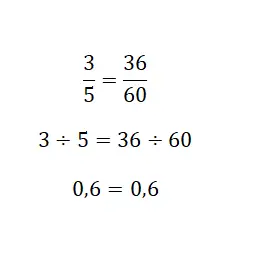
تمارين على الكسور المتكافئة
الآن بعد أن قرأت النظرية بأكملها، يمكنك محاولة حل التمارين التالية، مما سيسمح لك بإكمال فهم الشرح. ننصحك بمحاولة حلها بنفسك، وبمجرد حصولك عليها، قم بمقارنة نتيجتك بالنتيجة التي نقدمها لك. ومع ذلك، نسمح لك بالتدرب على:
التمرين 1
ابحث عن كسر مكافئ عن طريق التبسيط لكل كسر نقدمه:
لحل هذا التمرين، ما عليك سوى تطبيق تبسيط الكسور، وبالتالي الحصول على الكسر غير القابل للاختزال المكافئ. الأمثلة الأربعة متشابهة جدًا، لذا لا توجد صعوبة كبيرة في حلها.
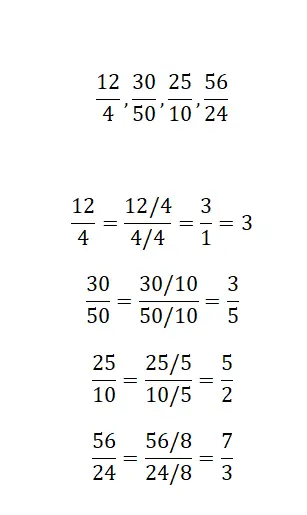
تمرين 2
ابحث عن كسر مكافئ بالتضخيم لكل كسر نقترحه:
بعد ذلك، سيتعين عليك تضخيم الكسور التي نقترحها، وبهذه الطريقة ستحصل على كسور مكافئة أكبر. لا يهم الرقم الذي تستخدمه لإجراء الضرب، على سبيل المثال، سنفعل ذلك مع 2 و 3.
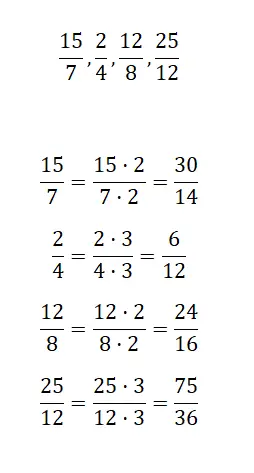
التمرين 3
حدد ما إذا كانت الكسور التالية متكافئة أم لا:
لمعرفة ما إذا كان الكسران متكافئين أم لا، عليك استخدام إحدى الطرق الثلاث التي شرحناها أعلاه. سوف تجد الإصلاحات قد تم حلها من خلال الإجراء الأول، على الرغم من أنك حر في استخدام النظام الذي تريده.
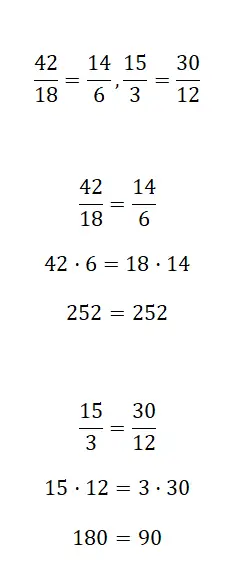
التمرين 4
احسب الكسور المكافئة للتعبيرات التالية:
في هذا التمرين الأخير، سيتعين عليك إعادة كتابة التعبيرات التي نقترحها ( الأعداد الصحيحة والأعداد الكسرية) في صورة كسر، في محاولة للحفاظ على علاقة التكافؤ.