الكسور الجبرية: التبسيط، العمليات، التمارين المحلولة، إلخ. -

نشرح في هذه الصفحة ما هي الكسور الجبرية ومتى تكون متكافئة وكيفية تبسيطها وكيفية إجراء العمليات على الكسور الجبرية (الجمع والطرح والضرب والقسمة). بالإضافة إلى ذلك، ستتمكن من رؤية حل التمارين خطوة بخطوة للكسور الجبرية. باختصار، ستجد هنا كل ما يتعلق بالكسور الجبرية.

ما هي الكسور الجبرية؟

في الرياضيات، الكسر الجبري هو كسر له كثيرة حدود في البسط ومتعددة حدود أخرى في المقام.

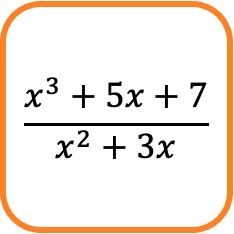
على سبيل المثال، التعبير الكسري أعلاه يتكون من كسر جبري لأن بسطه ومقامه يتكونان من كثيرات الحدود.

معادل الكسر الجبري

بمجرد أن نعرف تعريف الكسور الجبرية، دعونا نرى متى يكون اثنان من هذه الكسور متساويين.

رياضياً، يكون كسران جبريان متكافئين إذا تحقق الشرط التالي:

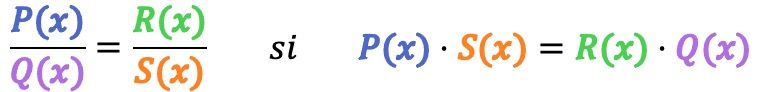
على سبيل المثال، سوف نتحقق مما إذا كان الكسران الجبريان التاليان متكافئين:

$\cfrac{x+3}{x^2+5x+6} \qquad \cfrac{1}{x+2}$

لتحديد ما إذا كانت الكسور متساوية جبريًا، نضرب حدودها عرضيًا:

$(x+3)\cdot (x+2) = (x^2+5x+6)\cdot 1$

الآن دعونا نحسب مضاعفات كثيرات الحدود:

$x^2+2x+3x+6 = x^2+5x+6$

$x^2+5x+6 = x^2+5x+6$

لقد حصلنا على التعبير نفسه في طرفي المعادلة، لذا فهما كسران جبريان متكافئان.

تبسيط الكسور الجبرية

لتبسيط كسر جبري، يجب عليك أولًا تحليل كثيرات الحدود في البسط والمقام، ثم حذف العوامل المشتركة بينهما.

من الواضح أنه لتبسيط الكسور الجبرية، من الضروري أن تعرف ما هو التحليل متعدد الحدود وكيف يتم ذلك. إذا كنت لا تزال لا تعرف كيفية تحليل كثيرات الحدود أو لا تتذكرها تمامًا، فإنني أوصي بالانتقال إلى الصفحة المرتبطة قبل المتابعة، وإلا فلن تفهم الإجراء إلا بالكاد. فهو يشرح خطوة بخطوة كيفية تحليل كثيرات الحدود إلى عوامل، وبالإضافة إلى ذلك، ستتمكن من رؤية العديد من الأمثلة والتدرب على التمارين التي تم حلها.

الآن دعونا نرى كيف يتم تبسيط الكسر الجبري من خلال تطبيق طريقة تحليل كثيرات الحدود باستخدام مثال:

بسّط الكسر الجبري التالي:

$\cfrac{x^3+2x^2-x-2}{x^2-2x+1}$

أولاً، نقوم بتحليل كثيرات الحدود لبسط ومقام الكسر:

$\cfrac{(x-1)(x+1)(x+2)}{(x-1)(x-1)}$

⬆(إذا كنت لا تعرف كيفية تحليل كثيرات الحدود، قم بإلقاء نظرة على الرابط أعلاه)⬆

وبمجرد أن نقوم بتحليل كثيرات الحدود، فإننا نحذف العوامل المشتركة بين البسط والمقام، أي أننا نحذف جميع الحدود المتكررة:

$\cfrac{\cancel{(x-1)}(x+1)(x+2)}{\cancel{(x-1)}(x-1)}$

وبالتالي فإن الكسر الجبري المبسط يبدو كما يلي:

$\cfrac{(x+1)(x+2)}{x-1}$

في هذه المشكلة، تم تحليل كثيرات الحدود للكسر الجبري من خلال إيجاد جذورها؛ ومع ذلك، في بعض الأحيان يمكن تحليل كثيرة الحدود مباشرة عن طريق أخذ العامل المشترك (طريقة أسرع بكثير). في هذا الرابط سترى ما يعنيه أخذ عامل مشترك من كثيرة الحدود، وسوف تكتشف كيفية تبسيط الكسر الجبري باستخدام عامل مشترك.

العمليات على الكسور الجبرية

مثل أي نوع من الكسور، يمكن أيضًا إجراء العمليات باستخدام الكسور الجبرية. على وجه التحديد، يمكن جمع الكسور الجبرية وطرحها وضربها وتقسيمها. نوضح أدناه خطوة بخطوة مع الأمثلة كيفية حساب كل نوع من العمليات.

جمع وطرح الكسور الجبرية

إن إجراء جمع وطرح الكسور الجبرية متطابق عمليًا، لذلك سنقوم بتحليلها معًا. سنرى أولا مثالا على كسرين جبريين مضافين، وفيما يلي سندرس الفرق بين طريقة طرح الكسور الجبرية.

إضافة الكسور الجبرية

تتم عملية جمع الكسور الجبرية بنفس الطريقة المتبعة مع الكسور العادية: قم أولًا بتبسيط الكسور إلى مقام مشترك ثم قم بإضافة البسطين.

دعونا نرى كيف تتم إضافة الكسور الجبرية باستخدام مثال:

$\cfrac{x}{x^2+2x+1} + \cfrac{3x}{x^2+x}$

نقوم أولاً بتحليل مقامات الكسور:

$\cfrac{x}{(x+1)(x+1)} + \cfrac{3x}{x(x+1)}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

نحتاج الآن إلى إيجاد المضاعف المشترك الأصغر للمقامات لتقليل الكسور إلى مقام مشترك.

نصيحة: يتم دائمًا تكوين lcm للمقامات من حاصل ضرب العوامل المشتركة بينها مرفوعة إلى الأس الأكبر مضروبًا في العوامل غير المشتركة .

على سبيل المثال، في حالتنا

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

القاسم المشترك بين المقامين مرفوعاً للأس الأكبر هو

$(x+1)^2.$

والعامل غير المشترك بين المقامين هو

$x.$

وبالتالي فإن lcm للمقامات في هذه الحالة هو:

$(x+1)^2 \cdot x$

وبالتالي فإن lcm للمقامات هو

$(x+1)^2 \cdot x,$

وبالتالي سيكون هذا هو المقام الجديد للكسرين.

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{}{x(x+1)^2} + \cfrac{}{x(x+1)^2}$

بمجرد العثور على القاسم المشترك، يجب علينا تعديل البسط. للقيام بذلك، نتبع نفس العملية المتبعة في إضافة الكسور العادية: لكل كسر نقسم lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

بين المقام الأصلي وضرب النتيجة في البسط:

$\cfrac{x(x+1)^2}{(x+1)^2} = \cfrac{x\cancel{(x+1)^2}}{\cancel{(x+1)^2}} = \color{red}\bm{x}$

$\cfrac{x(x+1)^2}{x(x+1)}= \cfrac{\cancel{x}(x+1)^\cancel{2}}{\cancel{x}\cancel{(x+1)}}=\color{blue} \bm{x+1}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{x \cdot \color{red}\bm{x} \color{black} }{x(x+1)^2} + \cfrac{3x \cdot \color{blue} \bm{(x+1)} \color{black}}{x(x+1)^2}$

والآن يمكننا جمع الكسرين معًا لأن لهما نفس المقام:

$\cfrac{x^2+3x(x+1)}{x(x+1)^2}$

وأخيرًا، نتعامل مع البسط. نقوم أولاً بعمل حاصل ضرب أحادية الحد ومتعددة الحدود:

$\cfrac{x^2 +3x\cdot x+ 3x\cdot 1 }{x(x+1)^2}$

$\cfrac{x^2 +3x^2 + 3x }{x(x+1)^2}$

بعد ذلك، نضيف المصطلحات المشابهة إلى البسط:

$\cfrac{4x^2 + 3x }{x(x+1)^2}$

عادة نكون قد وصلنا إلى هذه النقطة بالفعل، لكن إذا نظرنا إلى هذه المشكلة عن كثب، فيمكننا تبسيط الكسر الجبري بشكل أكبر عن طريق إزالة العامل المشترك من البسط. حتى الآن:

$\cfrac{x(4x + 3)}{x(x+1)^2}$

$\cfrac{\cancel{x}(4x + 3)}{\cancel{x}(x+1)^2}$

$\cfrac{4x + 3}{(x+1)^2}$

وبذلك نكون قد أكملنا بالفعل مجموع الكسرين الجبريين.

طرح الكسور الجبرية

لطرح الكسور الجبرية، يجب أن نتبع إجراءً مشابهًا لجمع الكسور الجبرية: أولًا نختصر الكسور إلى مقام مشترك، ثم نطرح البسطين.

دعونا نرى كيف يتم طرح الكسور الجبرية بمثال:

$\cfrac{2x}{x^2-x-6} - \cfrac{4x-3}{(x+2)^2}$

أولًا، علينا تحليل مقامي الكسرين:

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2}$

كما هو الحال مع طرح الكسور العادية، يجب علينا الآن حساب المضاعف المشترك الأصغر ( lcm ) للمقامات لتقليل الكسور إلى مقام مشترك. في هذه الحالة، lcm للمقامات هو

$(x+2)^2(x-3) ,$

وبالتالي سيكون هذا هو المقام الجديد للكسرين.

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{}{(x+2)^2(x-3)} + \cfrac{}{(x+2)^2(x-3)}$

الآن نطبق نفس العملية المتبعة في طرح الكسور العادية: لكل كسر نقسم lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

بين المقام الأصلي وضرب النتيجة في البسط:

$\cfrac{(x+2)^2(x-3)}{(x+2)(x-3)} = \cfrac{(x+2)^{\cancel{2}}\cancel{(x-3)}}{\canel{(x+2)}\cancel{(x-3)}} = \color{red}\bm{x+2}$

$\cfrac{(x+2)^2(x-3)}{(x+2)^2}= \cfrac{\cancel{(x+2)^2}(x-3)}{\cancel{(x+2)^2}}=\color{blue} \bm{x-3}$

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{2x\cdot \color{red}\bm{(x+2)} \color{black}}{(x+2)^2(x-3)} + \cfrac{(4x-3)\cdot \color{blue} \bm{(x-3)} \color{black}}{(x+2)^2(x-3)}$

نجمع الآن بين الكسرين الجبريين حيث أن لهما نفس المقام:

$\cfrac{2x(x+2)-(4x-3)(x-3)}{(x+2)^2(x-3)}$

ونعمل على البسط. نقوم أولاً بحل مضاعفات كثيرات الحدود:

$\cfrac{2x^2+4x-\bigl[4x^2-12x-3x+9\bigr]}{(x+2)^2(x-3)}$

من الأخطاء الشائعة جدًا عند طرح الكسور الجبرية هو نسيان وضع قوسين بعد إجراء عملية الضرب. سيكون هذا خطأ لأن الإشارة السالبة تؤثر على جميع العناصر الناتجة في المنتج، وليس فقط الحد الأول.

نقوم بتنفيذ العمليات بين قوسين:

$\cfrac{2x^2+4x-\bigl[4x^2-15x+9\bigr]}{(x+2)^2(x-3)}$

وهكذا، وبفضل الإشارة السالبة، نغير إشارة جميع المصطلحات الموجودة بين القوسين:

$\cfrac{2x^2+4x-4x^2+15x-9}{(x+2)^2(x-3)}$

وأخيرًا، نقوم بتجميع أحاديات الحد المتشابهة:

$\cfrac{-2x^2+19x-9}{(x+2)^2(x-3)}$

ضرب الكسور الجبرية

لضرب الكسور الجبرية، نقوم أولاً بتحليل جميع متعددات الحدود للكسور المذكورة، ثم نضرب البسط في بعضها البعض والمقامات في بعضها البعض، وأخيرًا، نقوم بتبسيط الكسر الذي تم الحصول عليه.

لذلك، يتم حساب حاصل ضرب الكسور الجبرية بنفس طريقة حساب حاصل ضرب الكسور العادية.

بعد ذلك، دعونا نرى كيفية ضرب كسرين جبريين بمثال:

$\cfrac{3x}{x^2+x-2} \cdot \cfrac{x^2-6x+5}{x+1}$

أولًا، عليك تحليل جميع كثيرات حدود الكسور، سواء البسط أو المقام:

$\cfrac{3x}{(x-1)(x+2)} \cdot \cfrac{(x-1)(x-5)}{x+1}$

الآن دعونا نضرب الكسور. للقيام بذلك، نضرب البسط والمقامات معًا:

$\cfrac{3x \cdot (x-1)(x-5)}{(x-1)(x+2)\cdot (x+1)}$

$\cfrac{3x(x-1)(x-5)}{(x-1)(x+2)(x+1)}$

وأخيرًا، نقوم بتبسيط العوامل المتكررة في المقام والبسط:

$\cfrac{3x\cancel{(x-1)}(x-5)}{\cancel{(x-1)}(x+2)(x+1)}$

وبالتالي فإن نتيجة الضرب هي:

$\cfrac{3x(x-5)}{(x+2)(x+1)}$

لا يمكن تبسيط الكسر أكثر من ذلك. وبذلك نكون قد انتهينا بالفعل من ضرب الكسور الجبرية.

تقسيم الكسور الجبرية

لحساب قسمة الكسور الجبرية ، نقوم أولاً بتحليل جميع كثيرات الحدود، ثم نضرب الكسور بشكل عرضي (البسط الأول في المقام الثاني والمقام الأول في البسط الثاني)، وأخيرًا، نقوم بتبسيط الكسر الجبري.

لذلك دعونا نرى بشكل أفضل كيفية تقسيم كسرين جبريين باستخدام مثال:

$\cfrac{x^3-7x-6}{2x^2-8} : \cfrac{x^2+2x+1}{6}$

الخطوة الأولى في قسمة كسرين جبريين هي تحليل جميع كثيرات الحدود المشاركة في العملية:

$\cfrac{(x+1)(x+2)(x-3)}{2(x-2)(x+2)} : \cfrac{(x+1)^2}{6}$

الآن نحن بحاجة إلى تقسيم الكسور. وللقيام بذلك نقوم بضرب الكسور عرضيا، أي يتم ضرب البسط الأول في المقام الثاني وستكون النتيجة بسط الكسر الجديد، وبنفس الطريقة يتم ضرب المقام الأول في البسط الثاني وستكون النتيجة مقام الكسر الجديد:

$\cfrac{(x+1)(x+2)(x-3)\cdot 6}{2(x-2)(x+2)\cdot (x+1)^2}$

$\cfrac{6(x+1)(x+2)(x-3)}{2(x-2)(x+2)(x+1)^2}$

نقوم بتبسيط العوامل المتكررة في المقام والبسط:

$\cfrac{6\cancel{(x+1)}\cancel{(x+2)}(x-3)}{2(x-2)\cancel{(x+2)}(x+1)^\cancel{2}}$

$\cfrac{6(x-3)}{2(x-2)(x+1)}$

ويمكننا تبسيط الكسر بشكل أكبر

$6:2 = 3.$

$\cfrac{3(x-3)}{(x-2)(x+1)}$

لا يمكن تبسيط الكسر أكثر من ذلك. لذلك، قمنا بالفعل بتقسيم الكسور الجبرية.

تمارين محلولة على الكسور الجبرية

نقدم لك أدناه العديد من التمارين التي تم حلها خطوة بخطوة حول الكسور الجبرية، حتى تتمكن من التدرب وبالتالي الانتهاء من فهم المفهوم. لا تنس أنه يمكنك طرح أي أسئلة لديك أدناه في التعليقات! 💬💬💬

التمرين 1

حدد ما إذا كانت الكسور الجبرية التالية متكافئة أم لا:

$\cfrac{x+3}{x^2-9} \qquad \cfrac{1}{x-3} \qquad \cfrac{x-3}{x^2+2x-3}$

انظر الحل

للتحقق مما إذا كان كسران جبريان متكافئين، يجب عليك ضربهما عرضيًا ومعرفة ما إذا كنت ستحصل على المساواة. لذلك سوف نتحقق أولاً من الكسر الأول والثاني:

$\cfrac{x+3}{x^2-9}= \cfrac{1}{x-3} \quad ?$

$(x+3)\cdot (x-3)=(x^2-9)\cdot 1$

نحل الهوية البارزة على يسار المعادلة:

$x^2-9=x^2-9$

✅

في هذه الحالة، حصلنا على المساواة، وبالتالي فإن الكسرين الأول والثاني متساويان جبريًا.

نطبق الآن نفس الإجراء مع الكسر الجبري الأول والثالث:

$\cfrac{x+3}{x^2-9}= \cfrac{x-3}{x^2+2x-3} \quad ?$

$(x+3)\cdot (x^2+2x-3)=(x^2-9)\cdot(x-3)$

$x^3+2x^2-3x+3x^2+6x-9=x^3-3x^2-9x+27$

$x^3+5x^2+3x-9=x^3-3x^2-9x+27$

❌

ومع ذلك، هذه المرة الكسور الجبرية لا تحقق المعادلة، لذا فإن الكسرين الأول والثالث مختلفان رياضيًا.

في الختام، الكسر الثالث يختلف عن الكسر الأول، وبالتالي فهو أيضًا غير متساوٍ مع الكسر الثاني، لأن الكسرين الأول والثاني متساويان.

$\cfrac{x+3}{x^2-9} = \cfrac{1}{x-3} \neq \cfrac{x-3}{x^2+2x-3}$

تمرين 2

بسّط الكسور الجبرية التالية:

$\text{A)} \ \cfrac{5x^2+10x}{11x}$

$\text{B)} \ \cfrac{x^2-4}{x^2+2x-8}$

$\text{C)} \ \cfrac{x^3-2x^2-3x}{x^2-3x}$

$\text{D)} \ \cfrac{x^3-3x+2}{x^3+4x^2+x-6}$

انظر الحل

لتبسيط كسر جبري، علينا تحليل كثيرات الحدود في البسط والمقام، ثم حذف العوامل المتكررة. حتى الآن:

$\text{A)} \ \begin{array}{l} \cfrac{5x^2+10x}{11x} =\cfrac{5x(x+2)}{11x} = \\[4ex] =\cfrac{5\cancel{x}(x+2)}{11\cancel{x}}= \cfrac{\bm{5(x+2)}}{\bm{11}}\end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{x^2-4}{x^2+2x-8} = \cfrac{(x-2)(x+2)}{(x-2)(x+4)}= \\[4ex] = \cfrac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}(x+4)}=\cfrac{\bm{x+2}}{\bm{x+4}}}\end{array}$

$\text{C)} \ \begin{array}{l} \cfrac{x^3-2x^2-3x}{x^2-3x} = \cfrac{x(x+1)(x-3)}{x(x-3)}}= \\[4ex] = \cfrac{\cancel{x} (x+1) \cancel{x-3}}{\cancel{x}\cancel{(x-3)}} = \cfrac{x+1}{1} = \\[4ex] = \bm{x+1}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^3-3x+2}{x^3+4x^2+x-6}=\cfrac{(x-1)^2(x+2)}{(x-1)(x+3)(x+2)}= \\[4ex] = \cfrac{(x-1)^{\cancel{2}}\cancel{(x+2)}}{\cancel{(x-1)}(x+3)\cancel{(x+2)}}=\cfrac{\bm{x-1}}{\bm{x+3}}\end{array}$

التمرين 3

احسب عمليات الجمع والطرح التالية للكسور الجبرية:

$\text{A)} \ \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6}$

$\text{B)} \ \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4}$

$\text{C)} \ \cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}$

$\text{D)} \ x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}$

انظر الحل

لجمع (أو طرح) كسور جبرية، يجب علينا أولًا تقليل الكسور إلى مقام مشترك، ثم إضافة (أو طرح) البسط. لذا:

$\text{A)} \ \begin{array}{l} \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6} = \cfrac{4}{x(x+2)} + \cfrac{3x-2}{(x+2)(x-3)} = \\[4ex] =\cfrac{4\cdot(x-3)}{x(x+2)\cdot (x-3)} + \cfrac{(3x-2)\cdot x}{(x+2)(x-3)\cdot x} = \cfrac{4\cdot(x-3) + (3x-2)\cdot x}{x(x+2)(x-3)} = \\[4ex] = \cfrac{4x-12 + 3x^2-2x}{x(x+2)(x-3)} = \cfrac{ \bm{3x^2+2x-12}}{\bm{x(x+2)(x-3)}} \end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4} = \cfrac{4x}{x(x+1)^2} - \cfrac{2}{(x+1)(x-4)}= \\[4ex] = \cfrac{4x \cdot (x-4)}{x(x+1)^2 \cdot (x-4)} - \cfrac{2 \cdot (x+1) \cdot x}{(x+1)^2(x-4)\cdot x}= \cfrac{4x \cdot (x-4) - 2 \cdot (x+1) \cdot x }{x(x+1)^2 (x-4) }= \\[4ex] = \cfrac{4x^2 -16x - 2 \cdot (x^2+x) }{x(x+1)^2 (x-4) }= \cfrac{4x^2 -16x - 2x^2 - 2x }{x(x+1)^2 (x-4) } =\\[4ex] =\cfrac{2x^2 -18x}{x(x+1)^2 (x-4)}=\cfrac{x(2x -18)}{x(x+1)^2 (x-4)}= \\[4ex] = \cfrac{\bm{2x -18}}{\bm{(x+1)^2 (x-4)}}\end{array}$

$\text{C)} \ \begin{array}{l}\cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}=\cfrac{7x}{(x-2)^2} + \cfrac{-5}{x-2}} = \\[4ex] = \cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)\cdot (x-2)}=\cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)^2}= \\[4ex] = \cfrac{7x + [-5\cdot (x-2)] }{(x-2)^2} =\cfrac{7x -5\cdot (x-2) }{(x-2)^2} = \\[4ex] = \cfrac{7x -5x+10 }{(x-2)^2} = \cfrac{ \bm{2x+10}}{\bm{(x-2)^2 } } \end{array}$

$\text{D)} \ \begin{array}{l} x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}=\cfrac{x}{1} +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}= \\[4ex] =x +\cfrac{-3x}{(x-2)(x+2)} - \cfrac{2x^3-1}{2(x+1)(x+2)}= \\[4ex] = \cfrac{x\cdot 2(x-2)(x+2)(x+1)}{1\cdot 2(x-2)(x+2)(x+1)} \ + \ \cfrac{-3x\cdot 2(x+1)}{(x-2)(x+2)\cdot 2(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x+1)(x+2)\cdot (x+1)}= \\[4ex] = \cfrac{ 2x(x-2)(x+2)(x+1)}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x(x+1)}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x-2)(x+2)(x+1)}= \\[4ex]= \cfrac{ 2x^4+2x^3-8x^2-8x}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x^2-6x}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{2x^4-4x^3-x+2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - (2x^4-4x^3-x+2)}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - 2x^4+4x^3+x-2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ \bm{6x^3-14x^2-13x-2}}{\bm{2(x-2)(x+2)(x+1)}}\end{array}$

التمرين 4

حل عمليات ضرب وقسمة الكسور الجبرية التالية:

$\text{A)} \ \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1}$

$\text{B)} \ \cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3}$

$\text{C)} \ \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}$

$\text{D)} \ \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2}$

انظر الحل

لضرب الكسور الجبرية، يجب علينا أولًا تحليل جميع كثيرات الحدود، ثم ضرب البسط والمقامات معًا، وفي النهاية تبسيط الكسر الناتج.

$\text{A)} \ \begin{array}{l} \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1} = \cfrac{(x+1)(x+4)}{7}\cdot \cfrac{x-1}{(x-1)(x+1)}\\[4ex] =\cfrac{(x+1)(x+4)\cdot (x-1)}{7 \cdot (x-1)(x+1)}=\cfrac{(x+1)(x+4) (x-1)}{7(x-1)(x+1)} = \\[4ex] = \cfrac{\cancel{(x+1)}(x+4)\cancel{ (x-1)}}{7\cancel{(x-1)}\cancel{(x+1)}} = \cfrac{\bm{x+4}}{\bm{7}}\end{array}$

$\text{B)} \ \begin{array}{l}\cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3} = \cfrac{3(x+2)(x+3)}{3x}\cdot \cfrac{(x-1)(x+2)}{(x-1)(x+1)(x+3)}= \\[4ex] =\cfrac{3(x+2)(x+3)\cdot (x-1)(x+2)}{3x\cdot (x-1)(x+1)(x+3)}=\cfrac{3(x+2)(x+3) (x-1)(x+2)}{3x (x-1)(x+1)(x+3)} = \\[4ex] = \cfrac{\cancel{3}(x+2)\cancel{(x+3)} \cancel{(x-1)}(x+2)}{\cancel{3}x \cancel{(x-1)}(x+1)\cancel{(x+3)}} = \cfrac{(x+2)(x+2)}{x (x+1)} = \\[4ex] = \cfrac{\bm{(x+2)^2}}{\bm{x (x+1)}}\end{array}$

من ناحية أخرى، لتقسيم الكسور الجبرية، فإننا نقوم أولاً بتحليل جميع كثيرات الحدود، ثم نضرب الكسور بشكل عرضي (البسط الأول في المقام الثاني والمقام الأول في البسط الثاني)، وأخيرًا، نقوم بتبسيط الكسر الجبري الموجود.

$\text{C)} \ \begin{array}{l} \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}= \cfrac{3x}{(x+5)^2}:\cfrac{2x}{(x-5)(x+5)}=\\[4ex] = \cfrac{3x\cdot (x-5)(x+5)}{(x+5)^2\cdot 2x}=\cfrac{3x(x-5)(x+5)}{2x(x+5)^2 }= \\[4ex] =\cfrac{3\cancel{x}(x-5)\cancel{(x+5)}}{2\cancel{x}(x+5)^\cancel{2}} = \cfrac{\bm{3(x-5)}}{\bm{2(x+5)}}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2} = \cfrac{(x+3)(x+5)}{4x}:\cfrac{(x-1)(x+5)}{2x^2}= \\[4ex] = \cfrac{(x+3)(x+5)\cdot 2x^2 }{4x \cdot (x-1)(x+5)} = \cfrac{2x^2 (x+3)(x+5)}{4x (x-1)(x+5)} = \\[4ex] = \cfrac{2x^{\cancel{2}}(x+3)\cancel{ (x+5)}}{4\cancel{x} (x-1)\cancel{ (x+5)}} =\cfrac{2x(x+3)}{4(x-1)} = \cfrac{\bm{x(x+3)}}{\bm{2(x-1)}}\end{array}$

ما رأيك في التفسير؟ هل أحببتها؟ أو هل لديك أي اقتراحات؟ 💬 أخبرنا برأيك في هذه الصفحة في التعليقات! نقرأ لكم جميعا! 👀 وما تنسوا إنكم كمان تقدروا تسألونا كل أسئلتكم! ❔👇❔👇

الكسور الجبرية: التبسيط، العمليات، التمارين المحلولة،…

ما هي الكسور الجبرية؟

معادل الكسر الجبري

تبسيط الكسور الجبرية

العمليات على الكسور الجبرية

جمع وطرح الكسور الجبرية

إضافة الكسور الجبرية

طرح الكسور الجبرية

ضرب الكسور الجبرية

تقسيم الكسور الجبرية

تمارين محلولة على الكسور الجبرية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد