القطع المكافئ (الرياضيات): التعريف، المعادلة، العناصر، الأمثلة،...

ستجد في هذه الصفحة كل شيء عن القطع المكافئ: ما هو، ماذا يمثل، عناصره (البؤرة، الدليل، الرأس، إلخ.) معادلته (مع الأنواع المختلفة لمعادلات القطع المكافئ)، أمثلة، تمارين محلولة، خصائصه، تطبيقاته،…

ما هو المثل؟

القطع المكافئ مفهوم له معاني مختلفة جدًا، لكن تعريفه الرياضي هو كما يلي:

في الرياضيات، القطع المكافئ هو موضع النقاط على المستوى التي تكون متساوية البعد عن نقطة ثابتة (تسمى البؤرة) وخط ثابت (يسمى الدليل).

ولذلك فإن أي نقطة في القطع المكافئ تكون على نفس المسافة من بؤرته ودليله.

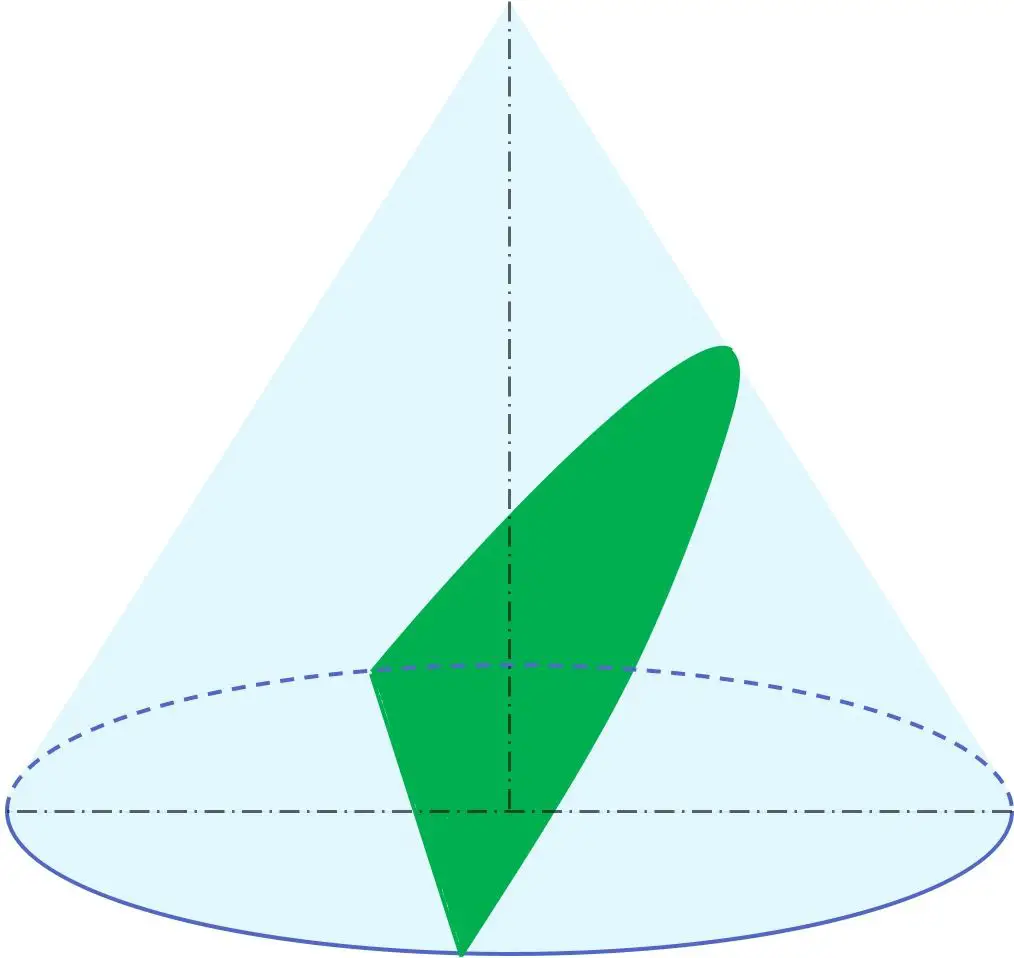
بالإضافة إلى ذلك، في الهندسة، القطع المكافئ هو أحد القطع المخروطية إلى جانب المحيط والقطع الناقص والقطع الزائد. وبعبارة أخرى، يمكن الحصول على القطع المكافئ من المخروط.

وعلى وجه الخصوص، ينتج القطع المكافئ من مقطع مخروط لمستوي بزاوية ميل بالنسبة إلى محور الدوران المكافئة لزاوية مولد المخروط. ولذلك، فإن المستوى الذي يحتوي على القطع المكافئ يكون موازيًا لمولد المخروط.

عناصر القطع المكافئ

تعتمد خصائص القطع المكافئ على العناصر التالية:

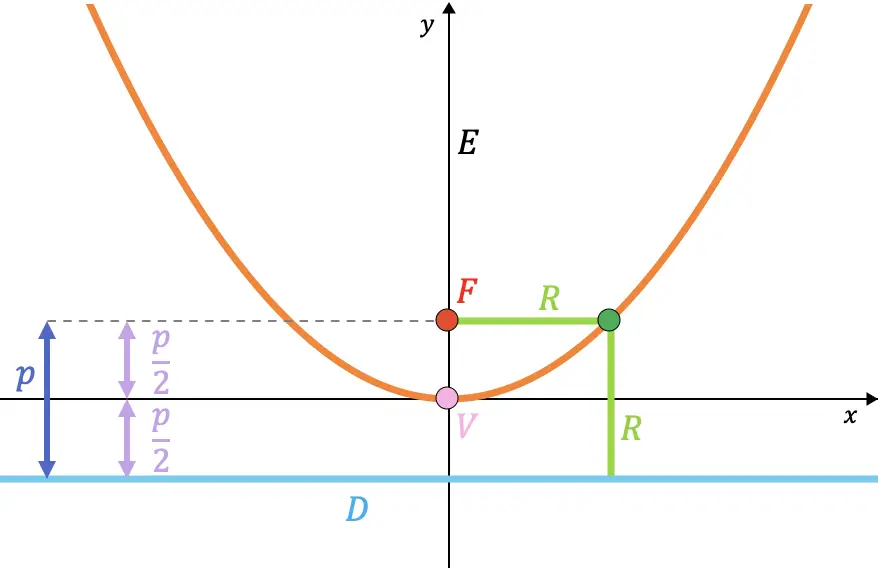
البؤرة (F) : هي نقطة ثابتة داخل القطع المكافئ. المسافة من أي نقطة من القطع المكافئ إلى البؤرة تساوي المسافة من نفس النقطة إلى دليل القطع المكافئ.
الدليل (D) : هو خط ثابت خارج القطع المكافئ. نقطة القطع المكافئ هي نفس المسافة من الدليل كما هي من بؤرة القطع المكافئ.
المعلمة (ع) : هي المسافة من البؤرة إلى المخرج.
متجه نصف القطر (R) : هو القطعة التي تربط نقطة القطع المكافئ بالبؤرة. وتتزامن قيمته مع المسافة من النقطة إلى الدليل.
المحور (E) : هو الخط المتعامد مع الدليل الذي يمر عبر التركيز وهو محور تماثل القطع المكافئ، في الرسم البياني أدناه يتوافق مع محور الكمبيوتر (المحور Y). ويسمى أيضا المحور البؤري.
الرأس (V) : هي نقطة التقاطع بين القطع المكافئ ومحوره.
البعد البؤري : هو المسافة بين البؤرة والرأس، أو بين الدليل والرأس. قيمتها تساوي دائما
$\displaystyle \frac{p}{2}.$

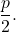
الجانب الأيمن

الجانب الأيمن من القطع المكافئ هو الوتر الموجود داخل القطع المكافئ الذي يمر عبر البؤرة ويكون موازيًا للدليل.

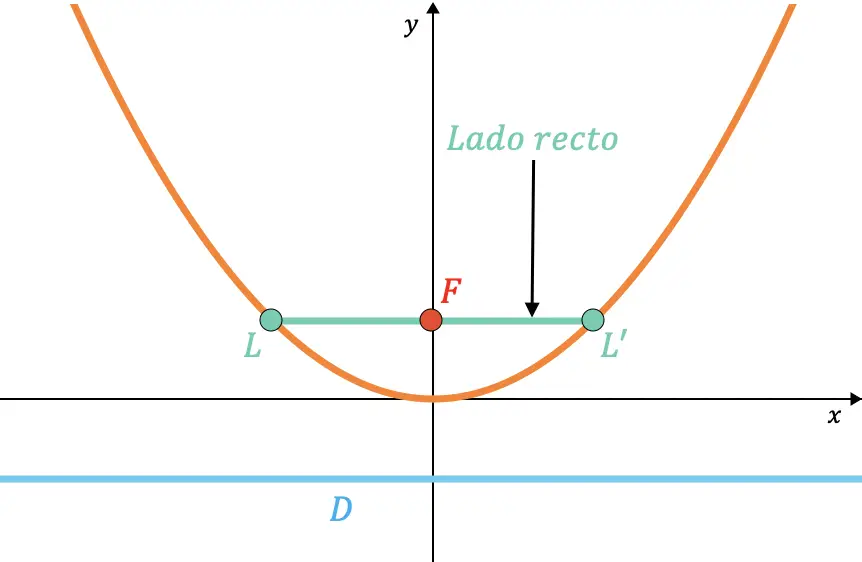
وبالمثل، يمكن إثبات أن طول الجانب الأيمن يكون دائمًا ضعف قيمة المعلمة

$p.$

$\lvert LL'\rvert = 2p$

من ناحية أخرى، فإن الخطين المماسين للقطع المكافئ الذي يمر عبر طرفي الجانب الأيمن يشكلان زاوية 45 درجة مع الجانب الأيمن نفسه ويتقاطعان أيضًا في الجزء العلوي من القطع المكافئ.

معادلات القطع المكافئ

معادلة القطع المكافئ هي نوع من الدالة التربيعية لأنها يجب أن تحتوي دائمًا على حد مربع واحد على الأقل. بالإضافة إلى ذلك، تعتمد معادلة القطع المكافئ على اتجاهه الأفقي أو الرأسي.

وهكذا، في الهندسة التحليلية، هناك عدة طرق للتعبير عن القطع المكافئ رياضيًا: المعادلة الأساسية أو المخفضة ، والمعادلة العادية ، والمعادلة العامة للقطع المكافئ.

المعادلة المختصرة أو الأساسية للقطع المكافئ

ما يميز المعادلة المختصرة أو القانونية عن المعادلات المكافئة الأخرى هو أن قمة القطع المكافئ هي أصل الإحداثيات ، أي النقطة (0,0).

يعتمد شكل المعادلة المخفضة للقطع المكافئ على ما إذا كان أفقيًا أم رأسيًا. انظر إلى التمثيل البياني التالي حيث تتم الإشارة إلى المتغيرات الأربعة المحتملة:

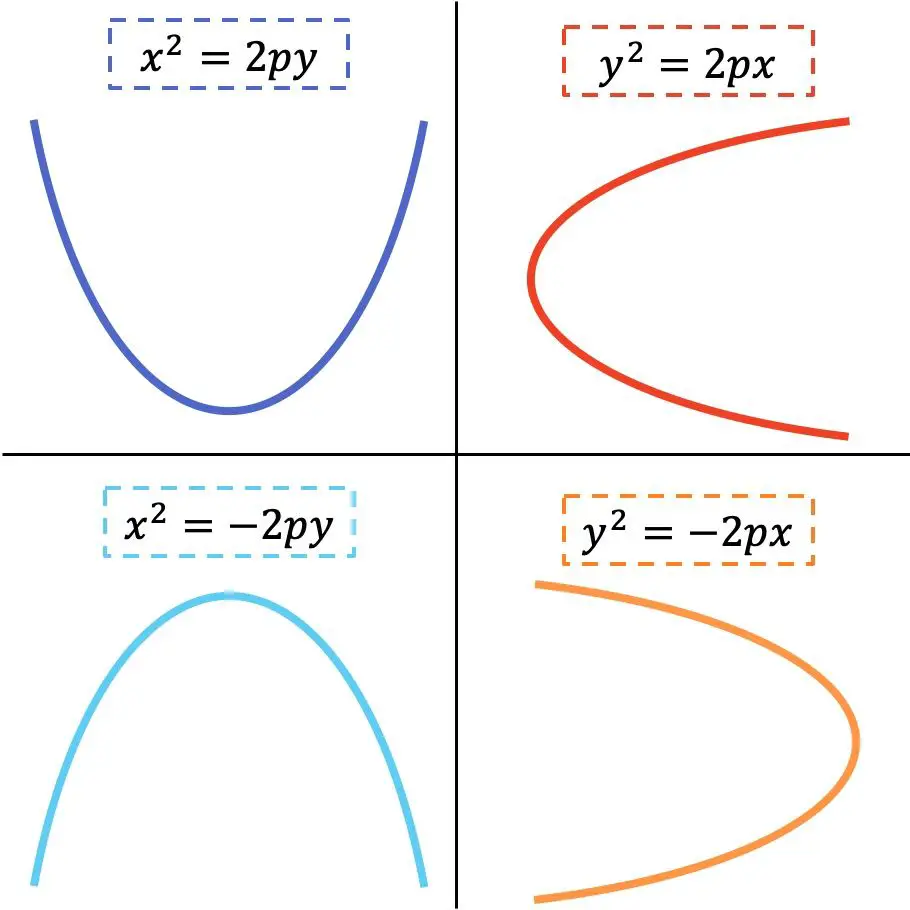
ذهب

$p$

هي المعلمة المميزة للقطع المكافئ.

كما ترون في الصورة السابقة، عندما يكون المتغير x مربعًا، يكون القطع المكافئ عموديًا، من ناحية أخرى، عندما يكون المتغير y مربعًا، يكون القطع المكافئ أفقيًا. ومن ناحية أخرى، فإن اتجاه فروع القطع المكافئ يعتمد على إشارة المعادلة.

المعادلة العادية للقطع المكافئ

لقد رأينا للتو كيف تبدو معادلة القطع المكافئ عندما يتوافق رأسه أو مركزه مع أصل الإحداثيات (المعادلة المخفضة أو القانونية)، ولكن ما هي معادلة القطع المكافئ إذا كان الرأس خارج “الأصل”؟

عندما يكون رأس القطع المكافئ أي نقطة، نستخدم المعادلة العادية للقطع المكافئ ، والتي يكون التعبير عنها:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}}(x-x_0 )^2 = 2p (y-y_0) \quad}$

حيث يكون مركز أو قمة القطع المكافئ هي النقطة

$V(x_0,y_0).$

المعادلة السابقة تتوافق مع القطع المكافئ الموجه عموديا، أي أن المحور البؤري للقطع المكافئ موازي للمحور Y.

وبالمثل، لتحديد القطع المكافئ المتجه أفقيًا (محوره البؤري موازٍ للمحور X)، يجب علينا استخدام المتغير التالي للمعادلة العادية للقطع المكافئ:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} (y-y_0 )^2 = 2p (x-x_0)\quad}$

حيث، كما في السابق، يكون مركز القطع المكافئ أو رأسه هو النقطة

$V(x_0,y_0).$

المعادلة العامة للقطع المكافئ

حتى الآن، يتم استخدام جميع معادلات القطع المكافئ التي قمنا بتحليلها للتعبير عن القطع المكافئ الأفقي أو الرأسي. ولكن من الواضح أن القطع المكافئ يمكن أيضًا أن يكون مائلًا أو مائلًا .

حسنًا، للتعبير عن هذا النوع من القطع المكافئ، نستخدم معادلة القطع المكافئ العامة ، وصيغتها كما يلي:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} Ax^2 + Bxy+Cy^2 +Dx+Ey + F = 0 \quad}$

المعادلة أعلاه هي قطع مكافئ إذا وفقط إذا كانت المعاملات

$A$

$C$

ليست صفرًا في نفس الوقت، وعلاوة على ذلك، يتم استيفاء الشرط التالي:

$B^2-4AC =0$

مثال لكيفية إيجاد الرأس والبؤرة ودليل القطع المكافئ من معادلته

في العديد من التمارين والمسائل المتعلقة بالقطع المكافئ، يُطلب منك حساب الرأس والبؤرة والدليل لقطع مكافئ معين. لذلك دعونا نرى كيف يتم ذلك من خلال مثال:

أوجد الرأس والبؤرة والدليل للقطع المكافئ التالي:

$x^2 = 4y$

الشيء الأساسي لحل هذا النوع من مسائل القطع المكافئ هو تحديد المعلمة p للقطع المكافئ . في هذه الحالة، تتوافق معادلة القطع المكافئ مع المعادلة المختصرة أو الأساسية (القطع المكافئ العمودي):

$x^2 = 2py$

وبالتالي فإن المعلمة p هي:

$2p = 4$

$p = \cfrac{4}{2}$

$p = 2$

من ناحية أخرى، بما أن القطع المكافئ يتبع المعادلة المختصرة أو القانونية، فهذا يعني أن رأسه أو مركزه يقع في أصل الإحداثيات:

$\bm{V(0,0)}$

بمجرد أن نعرف قيمة الرأس والمعلمة للقطع المكافئ، يمكننا بسهولة العثور على بؤرته ودليله.

الحد التربيعي للمعادلة هو المتغير x بحيث يكون محور القطع المكافئ موازيًا للمحور OY، وفي الواقع، بما أن رأسه هو النقطة (0,0)، فإن محور القطع المكافئ سيكون OY المحور نفسه. ومن ثم، فإن بؤرة القطع المكافئ تقع دائمًا على محور القطع المكافئ وعلى مسافة قدرها

$p/2$

من أعلى القطع المكافئ، فإن إحداثياته هي:

$\displaystyle F\left(0, \frac{p}{2} \right)$

$\displaystyle F\left(0, \frac{2}{2} \right)$

$\displaystyle \bm{F\left(0,1 \right)}$

وبالمثل، فإن المبدأ التوجيهي سيكون الخط الأفقي الذي هو على مسافة

$p/2$

من قمة القطع المكافئ، وهو أصل الإحداثيات. وبالتالي فإن معادلة الخط ستكون:

$y=-\cfrac{p}{2}$

$y=-\cfrac{2}{2}$

$\bm{y=-1}}$

تم رسم القطع المكافئ بيانيًا أدناه حتى تتمكن من التحقق من النتائج:

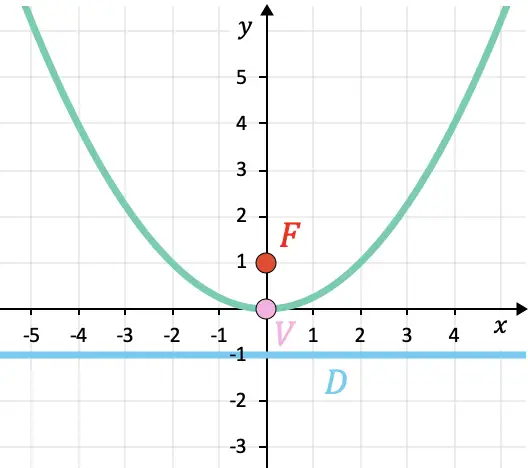
خصائص القطع المكافئ

جميع القطع المكافئة لها الخصائص التالية:

القطع المكافئ هو منحنى مفتوح، أو بمعنى آخر، يتكون من فرعين لا توجد نقاط مشتركة بينهما ويمتدان بشكل غير محدود.
كل قطع مكافئ له محور تماثل فريد، حيث تقع قمة القطع المكافئ المذكور.
القطع المكافئ المتجه عموديًا يكون محدبًا عندما ترتفع فروعه؛ على العكس من ذلك، يكون القطع المكافئ مقعرًا إذا نزلت فروعه إلى الأسفل.
إن انحراف القطع المكافئ يساوي الوحدة (١). الانحراف هو معامل يتم حسابه في هذه الحالة عن طريق قسمة المسافة من البؤرة إلى مركز القطع المكافئ على المسافة من الرأس إلى الدليل (وتتطابق المسافتان دائمًا في قيمتهما).
ويترتب على الخاصية السابقة أن جميع القطع المكافئة متشابهة أو متشابهة.
القطع المكافئ ليس له خطوط تقارب.

تطبيقات مكافئة

الآن بعد أن أصبحت على دراية تامة بمعنى المثل، ربما تتساءل… ما هو المغزى من المثل؟

حسنًا، حتى لو لم يبدو الأمر كذلك بالنسبة لك، فإن الشكل الهندسي للقطع المكافئ شائع جدًا في الحياة الواقعية. على سبيل المثال، في كثير من الأحيان عند رمي الكرة فإنها تقوم بحركة مكافئة، خاصة في كرة السلة. حسنًا، معادلة القطع المكافئ مفيدة جدًا في الدراسة التحليلية للمسار المكافئ الذي تتبعه الكرة.

هناك تطبيق آخر للطبق يتعلق بالهوائيات (ومن هنا جاء اسم الهوائي المكافئ). وبما أن كل شعاع يسقط على جسم ذو شكل مكافئ موازي لمحور التماثل ينعكس مباشرة باتجاه البؤرة، أي أن جميع الأشعة التي تذهب إلى الهوائي المكافئ تتركز عند البؤرة ويمكن استخدام ذلك بطرق مختلفة. هذا هو سبب أهمية التركيز في المثل.

مشاكل الطبق الثابتة

التمرين 1

احسب رأس القطع المكافئ وبؤرته ودليله ومعادلته كما يلي:

$y^2 = 8x$

انظر الحل

أولاً، سيكون القطع المكافئ أفقيًا لأنه يتبع التعبير التالي للمعادلة المختصرة أو الأساسية للقطع المكافئ:

$y^2 = 2px$

لذا فإن المعلمة p هي:

$2p = 8$

$p = \cfrac{8}{2}$

$p = 4$

$\bm{V(0,0)}$

بمجرد أن نعرف قيمة الرأس والمعلمة للقطع المكافئ، يمكننا بسهولة حساب بؤرته ودليله.

الحد التربيعي للمعادلة هو المتغير، أي أن محور القطع المكافئ سيكون موازيًا لمحور OX، وفي الواقع، بما أن رأسه هو النقطة (0,0)، فإن محور القطع المكافئ سيكون محور الثور نفسه ومن ثم، فإن بؤرة القطع المكافئ تقع دائمًا على محور القطع المكافئ وعلى مسافة قدرها

$p/2$

من أعلى القطع المكافئ، وإحداثياته هي:

$\displaystyle F\left(\frac{p}{2},0\right)$

$\displaystyle F\left(\frac{4}{2},0\right)$

$\displaystyle \bm{F\left(2,0 \right)}$

وبالمثل، فإن المبدأ التوجيهي على مسافة

$p/2$

من قمة القطع المكافئ الذي هو أصل الإحداثيات وهو متعامد مع محوره البؤري. وبالتالي فإن معادلة الخط الموجه هي:

$x=-\cfrac{p}{2}$

$x=-\cfrac{4}{2}$

$\bm{x=-2}}$

تمرين 2

أوجد رأس القطع المكافئ وبؤرته ودليله ومعادلته كما يلي:

$(x-4)^2 = -16(y+1)$

انظر الحل

يتم تعريف القطع المكافئ وفقًا لمعادلته العادية (المحور الموازي للمحور Y)، والتي تكون صيغتها:

$(x-x_0 )^2 = 2p (y-y_0)$

لذا فإن المعلمة p هي:

$2p = -16$

$p =- \cfrac{16}{2}$

$p =- 8$

من ناحية أخرى، في هذه الحالة، تشير المعادلة العادية للقطع المكافئ إلى أن مركزه ليس عند أصل الإحداثيات، ومن ناحية أخرى، فإن الإحداثيات الديكارتية لرأس القطع المكافئ هي الأرقام الموجودة بين قوسين مع تغيير إشارتها :

$\bm{V(4,-1)}$

بمجرد أن نعرف قيمة الرأس والمعلمة للقطع المكافئ، يمكننا حساب بؤرته ودليله.

الحد التربيعي للمعادلة هو المتغير x بحيث يكون محور القطع المكافئ موازيًا للمحور OY. وبالتالي، فإن بؤرة القطع المكافئ تقع دائمًا على محور القطع المكافئ وعلى مسافة قدرها

$p/2$

من قمة القطع المكافئ، بحيث تكون إحداثيات النقطة البؤرية هي إحداثيات الرأس عن طريق الجمع

$p/2$

عموديا:

$\displaystyle F\left(4,-1+\frac{p}{2}\right)$

$\displaystyle F\left(4,-1+\frac{-8}{2}\right)$

$\displaystyle F\left(4,-1-4\right)$

$\displaystyle \bm{F\left(4,-5 \right)}$

وبالمثل، سيكون الدليل هو الخط الأفقي الموجود على مسافة

$p/2$

من أعلى القطع المكافئ. وبالتالي فإن معادلة الخط الموجه هي:

$y=-1-\cfrac{-p}{2}$

$y=-1-\cfrac{-8}{2}$

$y=-1+4$

$\bm{y=3}}$

التمرين 3

تحديد المعادلة المكافئة التي محورها موازي لمحور الإحداثي السيني، ورأسها النقطة V(5,2) وتركيزها النقطة P(8,2).

انظر الحل

في هذه الحالة، رأس القطع المكافئ ليس هو أصل الإحداثيات، لذلك نحتاج إلى المعادلة العادية لتحديد القطع المكافئ في العبارة. كما أن المحور البؤري للقطع المكافئ موازي للمحور السيني، مما يعني أن القطع المكافئ سيكون متجهًا أفقيًا (ستتجه الفروع إلى اليمين أو إلى اليسار) وبالتالي يجب أن يكون الحد التربيعي للمعادلة هو المتغير ذ :

$(y-y_0 )^2 = 2p (x-x_0)$