الفائدة المركبة هي ببساطة الفائدة التي يتم توليدها من الأموال التي لديك بالفعل وإضافتها إلى أصل المبلغ الأصلي. على الرغم من أن الأمر قد يبدو بسيطًا، إلا أن هناك العديد من العوامل التي يجب مراعاتها لحساب الفائدة المركبة بشكل فعال. وفي هذه المقالة سنشرحها لك جميعها.
حاسبة الفائدة المركبة
تتيح حاسبة الفائدة المركبة للمستخدمين حساب الفائدة المركبة على الاستثمار. على سبيل المثال، يمكن استخدامه لحساب الفائدة على الاستثمار . الآلة الحاسبة سهلة الاستخدام وتتطلب من المستخدم إدخال: المبلغ الأولي المستثمر، والمساهمة السنوية، وسعر الفائدة والفترة الزمنية.
ومن هذه البيانات، ستتمكن هذه الآلة الحاسبة من تحديد المبلغ النهائي الذي سيتم توليده من الاستثمار.
ما هي الفائدة المركبة؟
الفائدة المركبة هي سعر الفائدة المطبق على أصل الدين والفائدة المتزايدة. إنه مفهوم مختلف تمامًا عنالفائدة البسيطة ، حيث أن الأخير يوفر نموًا خطيًا للاستثمار. في حين توفر الفائدة المركبة نموا هائلا .
الصورة التالية توضح هذا الاختلاف.
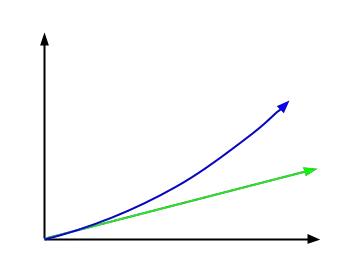
في الواقع، تعمل الفائدة المركبة من رأس المال الأولي بالإضافة إلى الفائدة التي اكتسبتها بالفعل. على سبيل المثال، إذا استثمرنا 5000 يورو وحصلنا على عائد بنسبة 7% في السنة الأولى، فسيكون لدينا رأس مال قدره 5350 يورو، حيث أن الفائدة ستولد 350 يورو.
ولكن، إذا حصلنا في العام التالي على نفس نسبة الربحية (7%)، فستزيد الفائدة من 350 يورو إلى 374.5 يورو. بعد ذلك، سيكون رأس المال الذي تم الحصول عليه هو 5,350 + 374.5 = 5,724.5 يورو. وهذا يعني أن الاهتمام يتزايد. ومع ذلك فإن الفائدة البسيطة تقدم نفس الفائدة كل عام.
كيف يتم حساب الفائدة المركبة؟
يعد حساب الفائدة المركبة عملية بسيطة نسبيًا. تحتاج فقط إلى معرفة أربعة متغيرات : المبلغ الأولي، والمساهمة السنوية، وسعر الفائدة ومدة الاستثمار (عادة بالسنوات). ثم عليك فقط تطبيق الصيغة التي نعرضها لك في القسم التالي:
صيغة الفائدة المركبة
يمكن استخدام صيغة الفائدة المركبة لحساب الفائدة المكتسبة على أصل أولي خلال فترة زمنية معينة. الصيغة هي كما يلي:
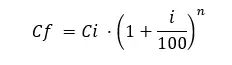
ذهب:
Cf = رأس المال النهائي الذي تم الحصول عليه مع الاستثمار.
ج = رأس المال الأولي.
i = معدل الفائدة السنوي معبرًا عنه كنسبة مئوية (ثم قم بتقسيم النسبة على مائة للحصول على النسبة المئوية بنسبة واحد).
ن = وقت الاستثمار.
ومع ذلك، هناك أيضًا صيغة أخرى يتم فيها أخذ “المساهمات السنوية” المتغيرة بعين الاعتبار. يجب عليك استخدامه فقط إذا كنت ترغب في تقديم مساهمات دورية للاستثمار. على سبيل المثال، تستثمر 1000 يورو في البداية، وبعد ذلك تستثمر 1000 يورو سنويًا. وبالتالي فإن الصيغة السابقة لن تناسبك، يجب عليك استخدام ما يلي:
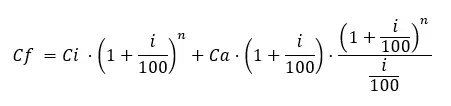
حيث تكون المتغيرات هي نفسها كما في الصيغة الأخرى ويتم إضافة Ca = المبلغ المساهم به سنويًا .
يبدو هذا التعبير الثاني أكثر تعقيدًا، لكنه في الواقع هو نفس الشيء تقريبًا. وفي الحقيقة فإن الصيغة السابقة هي التي تضيف ما تولده الاشتراكات السنوية.
مثال حقيقي لحساب الفائدة المركبة
تعتبر الفائدة المركبة أداة مفيدة للغاية لتحقيق الربح من الاستثمار. فيما يلي مثال لحساب الفائدة المركبة باستخدام الصيغة الأولى :
نفترض أن لديك 100 يورو في أحد البنوك التي تدفع فائدة سنوية بنسبة 5%. في نهاية السنة الأولى، سيكون لديك 105 يورو في حسابك، حيث أن البنك سيدفع لك 5 يورو كفائدة (5% من 100 يورو).
في بداية السنة الثانية، سيظل لديك مبلغ 105 يورو في حسابك، ولكن الآن يكتسب هذا المبلغ فائدة أكبر. بتعبير أدق، بفائدة سنوية 5%، سوف تكسب 5.25 يورو كفائدة (5% من 105). وهذا يعني أنه في نهاية السنة الثانية سيكون لديك إجمالي 110.25 يورو في حسابك.
وإذا كررنا هذه العملية، لبضع سنوات، سيتم توليد المزيد والمزيد من الاهتمام، لأنها عملية أسية . وبالتالي، نرى أن الفائدة المركبة تسمح لك بالحصول على عائد أعلى بكثير من الفائدة البسيطة على رأس المال الأولي.
ما هي مميزات الفائدة المركبة؟
ويمكن تلخيص فوائد الفائدة المركبة في جملة واحدة: “سوف تكسب المزيد من المال، إذا قمت بإعادة استثمار الأرباح”.
الفائدة المركبة هي “الفائدة على الفائدة” وهي أساس العديد من نماذج الاستثمار . إذا استثمرت 1000 يورو وحققت ربحًا بنسبة 10% سنويًا، فإن رأس المال المبدئي سيتضاعف ثلاث مرات تقريبًا بعد 10 سنوات إذا واصلت إعادة استثمار الأرباح. دون الحاجة إلى إضافة أي شيء آخر من جيبك.
مفتاح الاستفادة من الفائدة المركبة هو الانضباط والوقت . ابدأ بمبالغ صغيرة واستثمرها بانتظام؛ سترى كيف تنمو استثماراتك مع مرور الوقت.