العمليات مع وحيدات الحد

سبتمبر 17, 2023

في هذه الصفحة نشرح كيفية إجراء جميع العمليات على وحيدات الحد (الجمع والطرح والضرب والقسمة والقوة). بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة لكل نوع من العمليات باستخدام وحيدات الحد والتدرب على التمارين التي تم حلها خطوة بخطوة.

جمع وطرح أحاديات الحد

لا يمكن إضافة أو طرح اثنين أو أكثر من وحيدات الحد إلا إذا كانت أحادية الحد متشابهة، أي إذا كان لوحدتي الحد جزء متطابق حرفيًا (نفس الحروف ونفس الأسس).

ومن ثم، فإن مجموع (أو الطرح) لاثنين من أحاديات الحد المماثلة يساوي وحيدة حد أخرى مكونة من نفس الجزء الحرفي ومجموع (أو طرح) معاملات هاتين الحدتين.

يُطلق على جمع وطرح أحاديات الحد أيضًا اسم جمع وطرح أحاديات الحد على التوالي.

أمثلة على الجمع والطرح من وحيدات الحد

لكي تتمكن من فهم كيفية جمع وطرح اثنين أو أكثر من أحاديات الحد بوضوح، نترك لك عدة أمثلة أدناه:

$4x^6+3x^6 = 7x^6$
$5y^3-2y^3 = 3y^3$
$2x^2y+5x^2y-3x^2y = 4x^2y$
$6abc-7abc+4abc = 3abc$
$6x^3y^2-4x^3y+2x^2y^3 = \color{red} \bm{\times}$

لا يمكن جمع أو طرح أحاديات الحد في المثال الأخير لأنها غير متشابهة، أو بمعنى آخر، لها مجهولات أو أسس مختلفة.

منتج عدة مرات أحادية الحد

لحل منتج أحادية الحد برقم، ما عليك سوى ضرب معامل أحادية الحد بهذا الرقم، مع ترك الجزء الحرفي من أحادية الحد كما هو.

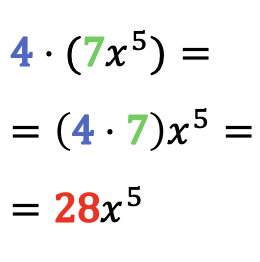
أمثلة على ضرب الأعداد بوحيدات الحد

$2\cdot (6x^3) = (2\cdot 6)x^3 = 12x^3$
$-4\cdot (5x^7) = (-4\cdot 5)x^7 = -20x^7$
$5\cdot (-3a^4b) = (5\cdot (-3))a^4b = -15a^4b$
$-7(-6x^9y^5)= (-7\cdot (-6))x^9y^5=42x^9y^5$

ضرب أحاديات الحد

نتيجة ضرب وحدتين هي وحيدة حد أخرى معاملها هو حاصل ضرب معاملات وحيدات الحد ويتم الحصول على الجزء الحرفي منها بضرب المتغيرات التي لها نفس الأساس، أي بجمع أسسها.

لذلك، لضرب وحدتين مختلفتين، يجب علينا ضرب المعاملات بينهما وإضافة أسس القوى التي لها نفس الأساس.

ومع ذلك، إذا ضربنا وحدتين لهما قوة أساسية مختلفة ، فسنحتاج ببساطة إلى ضرب معاملاتهما معًا وترك القوى كما هي. على سبيل المثال:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

ومن ناحية أخرى، عند ضرب أحاديات الحد، يجب مراعاة قاعدة العلامات:

وحيدة الحد الموجبة مضروبة في أحادية الحد الموجبة تعطي أحادية حد موجبة أخرى.
وحيدة الحد الموجبة مضروبة في أحادية الحد السالبة (أو العكس) تساوي أحادية الحد السالبة.
اثنين من أحاديات الحد السالبة مضروبة معًا تؤدي إلى ظهور أحادية حد موجبة.

أمثلة على الضرب أحادي الحد

فيما يلي عدة أمثلة للضرب بين أحاديات الحد حتى تتمكن من رؤية كيفية القيام بذلك:

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

كما رأيت، فإن حل عملية ضرب أحاديات الحد أمر بسيط نسبيًا. لكن يجب أن تضع في اعتبارك أن أحاديات الحد يمكن أيضًا ضربها في كثيرات الحدود، ويمكن ضرب متعددات الحدود حتى أو أكثر معًا. إذا كنت مهتمًا أكثر، يمكنك معرفة كيفية عمل كل هذه العمليات من خلال النقر على الضرب متعدد الحدود .

تقسيم أحاديات الحد

في الرياضيات، نتيجة تقسيم وحيدات الحد هي وحيدة حد أخرى معاملها يعادل خارج معاملات وحيدات الحد ويتم الحصول على الجزء الحرفي منها بقسمة المتغيرات التي لها نفس الأساس، أي بطرح أسسها .

من الواضح أنه يمكن أيضًا التعبير عن أي تقسيم لمونوميلات الحد ككسر:

$8x^3y^2z : 2x^2y = \cfrac{8x^3y^2z}{2x^2y} = 4xyz$

كما هو الحال في الضرب، في قسمة وحيدات الحد، من الضروري تطبيق قانون العلامات:

وحدة الحد الموجبة مقسومة على وحدة الحد الموجبة تعطي وحدة حد موجبة أخرى.
وحيدة الحد الموجبة مقسومة على أحادية الحد السالبة (أو العكس) تعادل أحادية الحد السالبة.
اثنين من أحاديات الحد السالبة مقسومة على بعضها البعض تؤدي إلى ظهور أحادية حد موجبة.

أمثلة على تقسيم أحاديات الحد

يمكنك رؤية المزيد من الأمثلة حول كيفية تقسيم اثنين أو أكثر من أحاديات الحد أدناه:

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

من المؤكد أنه في مرحلة ما، عندما تعلمت شيئًا جديدًا في الرياضيات، سألت نفسك: ما الغرض منه ؟ حسنًا، يتم استخدام قسمة أحادية الحد لتقسيم كثيرات الحدود. في الواقع، من الشائع جدًا ارتكاب خطأ عند تقسيم كثيرات الحدود لأنه تم تقسيم اثنين من أحاديات الحد بشكل غير صحيح. لهذا السبب نوصي، الآن بعد أن أصبحت على دراية بالتقسيم بين أحاديات الحد، أن ترى كيف يتم حساب تقسيم كثيرات الحدود ، لأنه الآن سيكون من الأسهل عليك تعلم الإجراء (إنه معقد للغاية).

قوة أحادية الحد

في الرياضيات، لحساب قوة أحادية الحد، يتم رفع كل عنصر من عناصر أحادية الحد إلى أس القوة . بمعنى آخر، قوة أحادية الحد تتكون من رفع معاملها ومتغيراتها (الحروف) إلى أس القوة.

تذكر من خصائص القوى أنه عندما يرفع كل منهما حدًا مرتفعًا بالفعل، تتضاعف الأسس. ولهذا السبب ، بالنسبة لقوة أحادية الحد، يتم دائمًا ضرب أس كل حرف في الأس الذي يشير إلى القوة .

من ناحية أخرى، لتنفيذ هذه العملية بشكل صحيح يجب أن تتذكر الخاصية التالية للقوى:

أحادية الحد السالبة المرفوعة إلى أس زوجي تعادل أحادية الحد الموجبة.
وبدلاً من ذلك، فإن أحادية الحد السالبة المرفوعة إلى أس فردي تؤدي إلى وحيدة حد سالبة.

أمثلة على صلاحيات monomials

نتركك مع بعض الأمثلة حتى تتمكن من فهم كيفية حساب قوة أحادية الحد بوضوح:

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

العمليات جنبا إلى جنب مع وحيدات الحد

بمجرد أن ترى ما هي جميع العمليات مع وحيدات الحد، تعرف أنه يمكن أيضًا دمجها مع بعضها البعض. وهذا يعني أنه يمكننا العثور على تمارين يُطلب منا فيها حل العمليات التي تحتوي على وحيدات الحد والتي تتضمن جميع أنواعها: الجمع والطرح والضرب والقسمة والقوى.

لكن لا تقلق، فهي ليست صعبة كما تبدو. الشيء الوحيد الذي عليك أن تتذكره هو الترتيب الذي يتم به حل العمليات المجمعة:

أولاً، تم حل العمليات التي تحتوي على وحيدات الحد بين قوسين.
ثم يتم حساب صلاحيات monomials.
ثالثا، يتم إجراء الضرب والقسمة من وحيدات الحد.
وأخيرًا، يتم تحديد عمليات الجمع والطرح من أحاديات الحد.

أنا متأكد من أنه من خلال حل المثال سوف تراه بشكل أكثر وضوحًا:

مثال على التشغيل المشترك لأحاديات الحد

$12x^9:(2x^4-8x^4)+3x^4\cdot 6x - (x^3\cdot 7x^2)$

أولًا، يجب علينا حل العمليات التي تحتوي على وحيدات الحد بين قوسين:

$12x^9:(-6x^4)+3x^4\cdot 6x - 7x^5$

وفي هذه الحالة ليس لدينا قوة. والآن دعونا نحسب مضاعفات وقسمة أحاديات الحد:

$-2x^5+18x^5 - 7x^5$

وأخيرًا، نجمع ونطرح أحاديات الحد:

$16x^5 - 7x^5$

$\bm{9x^5}$

تمارين محلولة على العمليات ذات الحدين

في حال كنت ترغب في التدرب، نترك لك أدناه عدة تمارين تم حلها خطوة بخطوة لصعوبة ESO على العمليات مع وحيدات الحد.

التمرين 1

احسب عمليات الجمع والطرح التالية من أحاديات الحد:

$\text{A)} \ 2x^4+9x^4$

$\text{B)} \ -3x^5y^3 +4x^5y^3$

$\text{C)} \ 3x^8-6x^8+2x^8$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2$

$\text{E)} \ 6xyz-5xz-7xyz-8xz$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3$

انظر الحل

$\text{A)} \ 2x^4+9x^4= \bm{11x^4}$

$\text{B)} \ -3x^5y^3 +4x^5y^3= \bm{x^5y^3}$

$\text{C)} \ 3x^8-6x^8+2x^8= \bm{-x^8}$

$\text{D)} \ -2a^3b^2-5a^3b^2+3a^3b^2-7a^3b^2+4a^3b^2=\bm{-7a^3b^2}$

$\text{E)} \ 6xyz-5xz-7xyz-8xz= \bm{-xyz-13xz}$

$\text{F)} \ 6y^3+2y^3-y^5+8y^4-y^5-5y^3 = \bm{-2y^5+8y^4+3y^3}$

تمرين 2

حل مضاعفات أحاديات الحد التالية:

$\text{A)} \ 5x^7\cdot 6x^2$

$\text{B)} \ 2y^8\cdot (-5y^6)$

$\text{C)} \ -4a^3 \cdot (-2a)$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6)$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)$

انظر الحل

$\text{A)} \ 5x^7\cdot 6x^2=(5\cdot 6)x^{7+2} = \bm{30x^9}$

$\text{B)} \ 2y^8\cdot (-5y^6)= (2\cdot (-5))y^{8+6} = \bm{-10y^{14}}$

$\text{C)} \ -4a^3 \cdot (-2a) =(-4\cdot (-2))a^{3+1} = \bm{8a^4}$

$\text{D)} \ 2x^3\cdot 4x \cdot (-3x^6) = 8x^4\cdot (-3x^6) = \bm{-24x^{10}}$

$\text{E)} \ -5x^6\cdot (-x^3) \cdot (-9x^4)=5x^9\cdot (-9x^4) =\bm{-45x^{13}}$

$\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-bb20ebb96e0dff759d07813f6fff9470_l3.png" height="22" width="195" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[35x^{11}y^2z^4\cdot (-2x^2y^5z^3) =\]" title="Rendered by QuickLaTeX.com"/> \bm{-70x^{13}y^7z^7}” title=”Rendered by QuickLaTeX.com”> <div class=$

التمرين 3

حدد نتيجة تقسيمات أحاديات الحد التالية:

$\text{A)} \ 24x^4: 6x^2$

$\text{B)} \ 16a^9: (-2a^6)$

$\text{C)} \ -21x^3:(-3x)$

$\text{D)} \ 14x^8y^3 :2x^6y$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)$

انظر الحل

$\text{A)} \ 24x^4: 6x^2 = (24:6)x^{4-2} = \bm{4x^2}$

$\text{B)} \ 16a^9: (-2a^6)= (16:(-2))a^{9-6} = \bm{-8a^3}$

$\text{C)} \ -21x^3:(-3x) = (-21:(-3))x^{3-1} = \bm{7x^2}$

$\text{D)} \ 14x^8y^3 :2x^6y = \bm{7x^2y^2}$

$\text{E)} \ 42x^5y^3z^6 : 7x^2y^3z^4= 6x^3y^0z^2=\bm{6x^3z^2}$

في العملية السابقة قمنا بتبسيط المصطلح

$y^0$

لأن أي رقم مرفوع إلى 0 يساوي 1. إذن:

$6x^3y^0z^2=6x^3\cdot 1 \cdot z^2=\bm{6x^3z^2}$

$\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)= <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-6dc0e068dbf84cef6abfe7e1789d245b_l3.png" height="22" width="194" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[-8x^4y^4z^6: (-4x^2y^2z^3)=\]" title="Rendered by QuickLaTeX.com"/> \bm{2x^2y^2z^3}” title=”Rendered by QuickLaTeX.com”> <div class=$

التمرين 4

أوجد قوى وحيدات الحد التالية:

$\text{A)} \ \left(-8x^4\right)^2$

$\text{B)} \ \left(-2a^7\right)^3$

$\text{C)} \ \left(5x^8y^2\right)^3$

$\text{D)} \ \left(-x^3y^5z\right)^6$

$\text{E)} \ \left(-2x^5y^4\right)^5$

انظر الحل

$\text{A)} \ \left(-8x^4\right)^2=(-8)^2\left(x^4\right)^2 = (-8)^2x^{4\cdot 2} = \bm{64x^{8}}$

$\text{B)} \ \left(-2a^7\right)^3=(-2)^3\left(a^7\right)^3 = (-2)^3a^{7\cdot 3} = \bm{-8a^{21}}$

$\text{C)} \ \left(5x^8y^2\right)^3=(5)^3\left(x^8y^2\right)^3 = \bm{125x^{24}y^6}$

$\text{D)} \ \left(-x^3y^5z\right)^6=(-1)^6\left(x^3y^5z\right)^6 = \bm{x^{18}y^{30}z^{6}}$

$\text{E)} \ \left(-2x^5y^4\right)^5 =(-2)^5\left(x^5y^4\right)^5 = \bm{-32x^{25}y^{20}}$

التمرين 5

حل العمليات التالية مع أحاديات الحد وبسطها قدر الإمكان:

$\text{A)} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$\text{B)} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$\text{C)} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$\text{D)} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$\text{E)} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

انظر الحل

$\color{blue} \mathbf{A}\bm{)} \color{black} \ 3x^2\cdot 4x^5 : 2x^4 + 10x^6:(-2x^4)\cdot 6x$

$12x^7 : 2x^4 -5x^2\cdot 6x$

$6x^3 -30x^3$

$\bm{-24x^3}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ 4\cdot \left(5x^4 -2x^4\right)^2$

$4\cdot \left(3x^4 \right)^2$

$4\cdot 9x^8$

$\bm{36x^8}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ 8x^7:(-4x^3+3x^3-7x^3)-5x^3\cdot 3x$

$8x^7:(-8x^3)-5x^3\cdot 3x$

$-x^4-15x^4$

$\bm{-16x^4}$

$\color{blue} \mathbf{D}\bm{)} \color{black} \ \left(-2x^2y\right)^3+4x^2 \cdot 5\left(xy\right)^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5\cdot x^4y^4:(-2y)$

$-8x^6y^3+4x^2 \cdot 5x^4y^4:(-2y)$

$-8x^6y^3+20x^6y^4:(-2y)$

$-8x^6y^3-10x^6y^3$

$\bm{-18x^6y^3}$

$\color{blue} \mathbf{E}\bm{)} \color{black} \ 8x^8:\left(-2x^3\right)^2-(7x^3\cdot 6x^6): (-2x^4)$

$8x^8:\left(-2x^3\right)^2-42x^9: (-2x^4)$

$8x^8:4x^6-42x^9: (-2x^4)$

$\bm{2x^2+21x^5}$

لا يمكن تبسيط العملية أكثر لأن أحاديتي الحد لهما أسس مختلفة، وبالتالي فإن النتيجة هي كثيرة الحدود.

إذا كنت قد وصلت إلى هذا الحد، فهذا يعني أنك قد أتقنت بالفعل جميع العمليات مع وحيدات الحد. ساطع! حسنًا، هناك عملية أخرى ستثير اهتمامك بالتأكيد وهي ضرب العدد. هذه عملية غريبة إلى حد ما، حيث يتم حسابها بشكل مختلف عن العمليات الأخرى. وفي الواقع، كثير من الناس لا يعرفون ما هو مضروب الرقم. تعرف على كيفية حل العامل بالضغط على هذا الرابط.

جمع وطرح أحاديات الحد

أمثلة على الجمع والطرح من وحيدات الحد

منتج عدة مرات أحادية الحد

أمثلة على ضرب الأعداد بوحيدات الحد

ضرب أحاديات الحد

أمثلة على الضرب أحادي الحد

تقسيم أحاديات الحد

أمثلة على تقسيم أحاديات الحد

قوة أحادية الحد

أمثلة على صلاحيات monomials

العمليات جنبا إلى جنب مع وحيدات الحد

مثال على التشغيل المشترك لأحاديات الحد

تمارين محلولة على العمليات ذات الحدين

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد