▷ كل ما يتعلق بالهندسة التحليلية في الفضاء ✅

ستجد في هذه الصفحة شرحًا لكل ما يتعلق بالهندسة التحليلية في الفضاء (والصيغ): معادلات الخط والمستوى، المواضع النسبية بين المستويات والخطوط، كيفية حساب المسافات والزوايا في الفضاء،…

ما هي الهندسة في الفضاء؟

هندسة الفضاء هي فرع الهندسة المسؤول عن دراسة الأشكال الهندسية ثلاثية الأبعاد، أي تلك التي تشغل مكانًا في الفضاء. مثل المخروط، المكعب، الهرم، الكرة، الاسطوانة، المنشور، متعددات الوجوه، الخ.

ومع ذلك، سنركز في هذه الصفحة على الهندسة التحليلية في الفضاء ، وهو جزء من الهندسة الفضائية الذي يركز على تحليل النقاط والخطوط والمستويات والمسافات بين شكلين هندسيين والزاوية التي يشكلونها ونقاط التقاطع بين الأشكال الهندسية المختلفة. الأرقام. العناصر، الخ.

معادلات الخط في الفضاء

تذكر أن التعريف الرياضي للخط هو مجموعة من النقاط المتتالية الممثلة في نفس الاتجاه بدون منحنيات أو زوايا.

وبالتالي، للتعبير رياضيًا عن أي خط في فضاء ثلاثي الأبعاد (في R3) نستخدم معادلات الخط، وللعثور عليها نحتاج فقط إلى نقطة تنتمي إلى الخط ومتجه الاتجاه للخط المذكور.

باستخدام هذين العنصرين الهندسيين فقط، يمكنك العثور على جميع المعادلات المختلفة للخط، وهي كما يلي:

معادلات الخط هي المعادلة المتجهة ، والمعادلات البارامترية ، والمعادلة المستمرة ، والمعادلة الضمنية (أو العامة) .

يوجد أدناه شرح للأنواع المختلفة لمعادلات الخط.

معادلة المتجهات للخط في الفضاء

نعم

$\vv{\text{v}}$

هو متجه الاتجاه للخط و

$P$

النقطة التي تنتمي إلى اليمين:

$\vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z) \qquad P(P_x,P_y,P_z)$

صيغة المعادلة المتجهية للخط هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=(P_x,P_y,P_z)+t\cdot (\text{v}_x,\text{v}_y,\text{v}_z) \end{empheq}$

المعادلات البارامترية للخط في الفضاء

يمكننا الحصول على صيغة المعادلة البارامترية للخط من معادلة المتجه الخاصة به عن طريق مساواة المكون بالمكون:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_x+t\cdot\text{v}_x \\[1.7ex] y=P_y+t\cdot\text{v}_y \\[1.7ex] z=P_z+t\cdot\text{v}_z\end{cases} \end{empheq}$

المعادلة المستمرة للخط في الفضاء

صيغة المعادلة المستمرة للخط هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_x}{\text{v}_x}=\cfrac{y-P_y}{\text{v}_y}= \cfrac{z-P_z}{\text{v}_z} \end{empheq}$

يمكن أيضًا الحصول على هذا النوع من معادلات الخط من المعادلات البارامترية، ويمكنك مشاهدة العرض التوضيحي للمعادلة المستمرة على صفحتنا، بالإضافة إلى ذلك، ستتمكن أيضًا من رؤية الأمثلة والتدريبات مع تمارين حل المعادلات من اليمين.

المعادلات العامة (أو الضمنية) للخط في الفضاء

أخيرًا، بضرب كسور المعادلة المستمرة للخط اثنين في اثنين، نحصل على المعادلات العامة (أو الضمنية) للخط :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} A_1x+B_1y+C_1z+D_1=0 \\[1.7ex] A_2x+B_2y+C_2z+D_2=0\end{cases} \end{empheq}$

يُسمى هذا النوع من معادلة الخط أيضًا بالمعادلة الديكارتية.

لقد رأينا للتو المعادلات الأربع الأكثر صلة بالخط (المتجه، البارامترى، المستمر والعامة)، ومع ذلك، هناك معادلة أخرى خاصة إلى حد ما، وبالتالي، يستغرق شرحها صفحة كاملة. هذه هي المعادلة الأساسية ، في هذا الرابط يمكنك رؤية شرحها الكامل، ولماذا هي مميزة جدًا وما الذي يجعلها مختلفة عن غيرها.

المعادلات الطائرة في الفضاء

في الهندسة التحليلية، معادلة المستوى هي معادلة تسمح بالتعبير عن أي مستوى تحليليًا. لذا، لإيجاد معادلة المستوى، فإنك تحتاج فقط إلى نقطة ومتجهين مستقلين خطيًا ينتميان إلى المستوى المذكور.

وبالتالي، فإن جميع أنواع معادلات المستوى هي: المعادلة المتجهة ، والمعادلات البارامترية ، والمعادلة الضمنية (أو العامة) ، والمعادلة القانونية (أو القطاعية) للمستوى.

بعد ذلك سنرى شرح وصيغة جميع معادلات الخطة.

معادلة المتجهات للطائرة

بالنظر إلى النقطة ومتجهي الاتجاه للمستوى:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

صيغة المعادلة المتجهة للمستوى هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}} \end{empheq}$

أو ما يعادلها:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

ذهب

$\lambda$

$\mu$

إنهما عددان قياسيان، أي عددان حقيقيان.

المعادلات البارامترية للطائرة

من ناحية أخرى، صيغة المعادلة البارامترية للمستوى هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases} \end{empheq}$

المعادلة الضمنية أو العامة للطائرة

يتم الحصول على المعادلة الضمنية للخطة، والتي تسمى أيضًا المعادلة العامة، عن طريق حل المحدد التالي وتحديد النتيجة على 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

وبالتالي فإن المعادلة الضمنية أو العامة للخطة الناتجة ستكون على الشكل التالي:

ويسمى هذا النوع من المعادلات المستوية أيضًا معادلة المستوية الديكارتية.

المعادلة الكنسي أو القطعي للطائرة

صيغة المعادلة الأساسية أو القطاعية للمستوى هي كما يلي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cfrac{x}{a}+\cfrac{y}{b} + \cfrac{z}{c} = 1 \end{empheq}$

ذهب:

$a$

هذه هي نقطة التقاطع بين المستوى والمحور X.
$b$

هذه هي نقطة التقاطع بين المستوى والمحور Y.
$c$

هذا هو المكان الذي يتقاطع فيه المستوى مع المحور Z.

ناقل طبيعي للطائرة

المتجه العمودي للمستوى هو متجه عمودي على جميع الخطوط الموجودة في هذا المستوى. ولذلك، فإن المتجه العمودي على المستوى يعني أنه عمودي على المستوى.

تتعلق العديد من المسائل المترية في الهندسة التحليلية المكانية بالمستويات ومتجهاتها العادية. لحل هذه التمارين، كل ما عليك فعله هو معرفة العلاقة الرياضية بين المستوى ومتجهه الطبيعي:

تتطابق المكونات X، Y، Z للمتجه الطبيعي للمستوى على التوالي مع المعاملات A، B، C للمعادلة الضمنية (أو العامة) للمستوى المذكور.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

ذهب

$\vv{n}$

هو المتجه المتعامد على المستوى

$\pi.$

المواقع النسبية لعنصرين هندسيين في الفضاء

من الواضح أن الخط أو المستوى ليس بالضرورة أن يكون بمفرده في الفضاء، بل على العكس من ذلك، يتفاعلان عادة مع بعضهما البعض: فهما يتقاطعان، ويكونان متوازيين، ومتعامدين، وما إلى ذلك. حسنًا، سنرى في هذا القسم المواضع النسبية المختلفة للخطوط والمستويات وكيفية تحديدها.

الموقع النسبي لخطين في الفضاء

في الهندسة التحليلية، عند العمل في مساحة ثلاثية الأبعاد (في R3) هناك 4 مواضع نسبية محتملة بين خطين: يمكن أن يكون الخطان عبارة عن خطوط متطابقة أو خطوط متوازية أو خطوط قاطعة أو خطوط قاطعة .

خطوط متوازية

يكون الخطان متوازيين إذا كان لهما نفس الاتجاه ولكن ليس بينهما نقطة مشتركة. بالإضافة إلى ذلك، الخطوط المتوازية تكون دائمًا على نفس المسافة من بعضها البعض.

الخطوط المتطابقة

يتطابق الخطان إذا كان لهما نفس الاتجاه وكانت جميع نقاطهما مشتركة.

خطوط التقاطع

خطان متقاطعان لهما اتجاهات مختلفة ولكنهما يتلامسان عند نقطة واحدة.

خطوط التقاطع

خطان متقاطعان لهما اتجاهات مختلفة ولا يتقاطعان في أي نقطة. وبالتالي فإن الخطين المتقاطعين ليسا في نفس المستوى. على سبيل المثال، في التمثيل الرسومي فوق السطر

$s$

يكون دائمًا أمام الخط المستقيم

$r$

، لذلك لن يلمسوا بعضهم البعض أبدًا.

كيفية العثور على الموضع النسبي لخطين حسب النطاقات

إحدى الطرق للعثور على الموضع النسبي لصفين هي حساب نطاقات مصفوفتين محددتين، كما سنرى أدناه. هذه الطريقة مفيدة جدًا عندما يتم التعبير عن الخطين في شكل معادلة ضمنية (أو عامة).

وبالتالي، إذا كان لدينا خطين معبرا عنهما بمعادلاتهما الضمنية (أو العامة) في فضاء ثلاثي الأبعاد (في R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

لتكن A هي المصفوفة المكونة من معاملات الخطين:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

وبالنظر إلى المصفوفة الموسعة A’، وهي المصفوفة المكونة من جميع معلمات الخطين:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

ومن ثم يمكن تحديد الموقع النسبي للمستقيمين بمدى المصفوفتين السابقتين حسب الجدول التالي:

لذلك، للعثور على الموضع النسبي بين صفين، سيتعين علينا حساب نطاقات كلتا المصفوفتين، واعتمادًا على نطاق كل مصفوفة، ستكون حالة واحدة أو أخرى.

يمكن إثبات هذه النظرية باستخدام نظرية روشيه-فروبينيوس (طريقة تستخدم لحل أنظمة المعادلات الخطية)، ولكن في هذه الصفحة لن نقوم بالبرهان لأنها مرهقة للغاية ولا تضيف الكثير. .

الموقع النسبي لطائرتين في الفضاء

في الهندسة التحليلية، هناك ثلاثة مواضع نسبية محتملة فقط بين مستويين: المستويات المتقاطعة، والمستويات المتوازية، والمستويات المتطابقة.

المستويات المتقاطعة : يتقاطع المستويان إذا تقاطعا على خط واحد فقط.
المستويان المتوازيان : يكون المستويان متوازيين إذا لم يتقاطعا في أي نقطة.
المستويان المتطابقان : يكون المستويان متطابقين إذا كانت بينهما جميع النقاط المشتركة.

لقطات متقاطعة

طائرات متوازية

خطط المطابقة

كيفية تحديد الموضع النسبي لطائرتين بواسطة المعاملات

إحدى طرق معرفة الموقع النسبي بين مستويين هي استخدام معاملات معادلاتهما العامة (أو الضمنية).

خذ بعين الاعتبار المعادلة العامة (أو الضمنية) لطائرتين مختلفتين:

$\pi_1 : \ Ax+By+Cz+D=0$

$\pi_2 : \ A'x+B'y+C'z+D'=0$

يعتمد الموقع النسبي بين المستويين في الفضاء ثلاثي الأبعاد على تناسب معاملاتهما أو معلماتهما:

وبالتالي، فإن المستويين سوف يتقاطعان عندما لا يتناسب أحد المعاملات A أو B أو C مع المعاملات الأخرى. ومن ناحية أخرى، سيكون المستويان متوازيين عندما تكون الحدود المستقلة فقط غير متناسبة. وأخيرًا، سيتطابق المخططان عندما تكون جميع معاملات المعادلتين متناسبة.

المسافات في الفضاء

ستجد أدناه الصيغ لحساب المسافة بين العناصر الهندسية المختلفة: بين نقطة وخط، بين مستويين، بين مستوى وخط،…

المسافة بين نقطتين

المسافة بين نقطتين تتوافق مع معيار المتجه الذي تحدده هاتان النقطتان.

فإذا كان لدينا نقطتان عامتان:

$A(a_x,a_y,a_z) \qquad \qquad B(b_x,b_y,b_z)$

صيغة المسافة بين النقطتين هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(A,B) = \vert \vv{AB} \rvert = \sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2} \end{empheq}$

المسافة من نقطة إلى خط

صيغة حساب المسافة من نقطة إلى خط في الفضاء هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert} \end{empheq}$

ذهب:

$\lvert \vv{\text{v}}_r \rvert$

هي وحدة متجه الاتجاه للخط

$r.$
$Q$

هي نقطة على اليمين

$r,$

$P$

نقطة على السطر

$s$

و

$\vv{QP}$

المتجه المحدد بالنقطتين
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

هو معامل المنتج المتجه بين المتجهات

$\vv{QP}$

و

$\vv{\text{v}}_r$

المسافة بين خطين

المسافة بين خطين تعتمد على موقعهما النسبي:

إذا تطابق الخطان أو تقاطعا ، فإن المسافة بين الخطين تساوي الصفر، لأنهما يتقاطعان (على الأقل) في نقطة واحدة.
عندما يكون الخطان متوازيين أو متقاطعين، يجب تطبيق صيغة حسب الحالة (كلا التوضيحين متوفرين أدناه).

المسافة بين خطين متوازيين

الخطان المتوازيان يفصل بينهما دائمًا نفس المسافة. لذا لحساب المسافة بين خطين متوازيين في الفضاء (في R3) يتم ذلك بنفس الطريقة كما في المستوى (في R2): كل ما عليك فعله هو أن تأخذ نقطة على أحد الخطين وتجد المسافة هناك. هو من هذه النقطة إلى الخط الآخر.

لذا، لتحديد المسافة بين خطين متوازيين، يجب عليك استخدام صيغة المسافة بين نقطة وخط.

المسافة بين خطين متقاطعين

ليكن متجه الاتجاه وأي نقطة من خطين متقاطعين:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

صيغة المسافة بين خطين متقاطعين هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} \end{empheq}$

ذهب:

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

هي القيمة المطلقة للمنتج المختلط للمتجهات

$\vv{\text{u}}, \vv{\text{v}}$

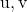
والمتجه المحدد بالنقاط

$A$

و

$B$

.
$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

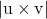
هو معامل حاصل الضرب المتجه بين متجهات الاتجاه للخطين المتقاطعين.

على الرغم من أن لديك الصيغة هنا، فإن تحديد المسافة بين خطين متقاطعين أكثر تعقيدًا مما يبدو. لذلك إذا أردت التدرب في الرابط التالي يمكنك مشاهدة أمثلة وتمارين محلولة على المسافة بين خطين متقاطعين.

المسافة من نقطة إلى الطائرة

بالنظر إلى نقطة والمعادلة العامة (أو الضمنية) للمستوى:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

صيغة المسافة من نقطة إلى مستوى هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}} \end{empheq}$

إذا حصلنا بتطبيق الصيغة على نتيجة تساوي صفرًا، فهذا يعني بوضوح أن المسافة بين النقطة والمستوى هي صفر، وبالتالي فإن النقطة جزء من هذا المستوى.

المسافة بين طائرتين

المسافة بين مستويين في الفضاء تعتمد على الموقع النسبي بين هذين المستويين:

وإذا كان المستويان متقاطعين أو متطابقين فإن المسافة بينهما تساوي صفراً لأنهما يتقاطعان عند نقطة معينة.
إذا كان المستويان متوازيين ، يتم حساب المسافة بين المستويين عن طريق أخذ نقطة من أحد المستويين وحساب المسافة بين تلك النقطة والمستوى الآخر.

المسافة بين طائرتين متوازيتين

المستويان المتوازيان يكونان دائمًا على نفس المسافة من بعضهما البعض، لذا لإيجاد المسافة بين مستويين متوازيين يمكننا أخذ نقطة على أحد المستويين وحساب المسافة من تلك النقطة إلى المستوى الآخر.

لذا، لحساب المسافة بين مستويين متوازيين، يجب عليك إيجاد نقطة على أحد المستويين ثم استخدام صيغة المسافة بين نقطة ومستوى.

الزوايا في الفضاء

كما هو الحال مع المسافات، فإن تحديد الزاوية بين جسمين هندسيين في الفضاء يعتمد على خصائصهما الهندسية. لأن حساب الزاوية التي يشكلها خطان ليس هو نفسه حساب الزاوية التي يشكلها مستويان. أدناه لديك الصيغ للعثور على الزوايا بين الخطوط والمستويات.

الزاوية بين خطين

لمعرفة الزاوية المحصورة بين خطين في الفضاء الإقليدي، يجب علينا حساب الزاوية التي تشكلها متجهات اتجاههما، وبالتالي:

بالنظر إلى متجهات الاتجاه لخطين مختلفين:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y,\text{u}_z)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

يمكن حساب الزاوية التي يشكلها هذين الخطين بالصيغة التالية:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

ذهب

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

هي وحدات من المتجهات

$\vv{\text{u}}$

$\vv{\text{v}}$

على التوالى.

تذكر أن صيغة معامل المتجه هي:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

الزاوية بين طائرتين

الزاوية بين طائرتين تساوي الزاوية التي تشكلها المتجهات العادية للطائرات المذكورة. لذلك، لإيجاد الزاوية بين مستويين، نحسب الزاوية التي تشكلها متجهاتها العادية، لأنها متكافئة .

بالنظر إلى المعادلة العامة (أو الضمنية) لطائرتين مختلفتين:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1=0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2=0$

المتجه الطبيعي لكل مستوى هو :

$\vv{n}_1=(A_1,B_1,C_1)$

$\vv{n}_2=(A_2,B_2,C_2)$

ويتم تحديد الزاوية التي تشكلها هاتان المستويتان من خلال حساب الزاوية التي تشكلها متجهاتها العادية باستخدام الصيغة التالية:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{n}_1 \cdot \vv{n}_2\rvert}{\lvert \vv{n}_1 \rvert \cdot \lvert \vv{n}_2 \rvert} \end{empheq}$

الزاوية بين الخط والمستوى

يتم تعريف الزاوية التي يشكلها الخط والمستوى على أنها أصغر الزاويتين المتكاملتين اللتين يشكلهما متجه اتجاه الخط والمتجه الطبيعي للمستوى.

لذلك، إذا

$\vv{\text{v}}$

هو متجه الاتجاه للخط و

$\vv{n}$

هو المتجه الطبيعي للطائرة:

$\vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

$\vv{n}=(n_x,n_y,n_z)$

الصيغة المستخدمة لحساب الزاوية التي يشكلها الخط والمستوى هي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \text{sen}(\alpha)=\cfrac{\lvert \vv{\text{v}} \cdot \vv{n}\rvert}{\lvert \vv{\text{v}} \rvert \cdot \lvert \vv{n} \rvert} \end{empheq}$

الهندسة التحليلية في الفضاء (الصيغ)

ما هي الهندسة في الفضاء؟

معادلات الخط في الفضاء

معادلة المتجهات للخط في الفضاء

المعادلات البارامترية للخط في الفضاء

المعادلة المستمرة للخط في الفضاء

المعادلات العامة (أو الضمنية) للخط في الفضاء

المعادلات الطائرة في الفضاء

معادلة المتجهات للطائرة

المعادلات البارامترية للطائرة

المعادلة الضمنية أو العامة للطائرة

المعادلة الكنسي أو القطعي للطائرة

ناقل طبيعي للطائرة

المواقع النسبية لعنصرين هندسيين في الفضاء

الموقع النسبي لخطين في الفضاء

كيفية العثور على الموضع النسبي لخطين حسب النطاقات

الموقع النسبي لطائرتين في الفضاء

كيفية تحديد الموضع النسبي لطائرتين بواسطة المعاملات

المسافات في الفضاء

المسافة بين نقطتين

المسافة من نقطة إلى خط

المسافة بين خطين

المسافة بين خطين متوازيين

المسافة بين خطين متقاطعين

المسافة من نقطة إلى الطائرة

المسافة بين طائرتين

المسافة بين طائرتين متوازيتين

الزوايا في الفضاء

الزاوية بين خطين

الزاوية بين طائرتين

الزاوية بين الخط والمستوى

اترك تعليقاً إلغاء الرد