الخط المقارب العمودي

ستجد هنا الخطوط المقاربة الرأسية للدالة (مع أمثلة). سنشرح أيضًا كيفية العثور على الخطوط المقاربة الرأسية للدالة، وبالإضافة إلى ذلك، ستتمكن من التدرب على التمارين التي تم حلها خطوة بخطوة.

ما هو الخط المقارب العمودي؟

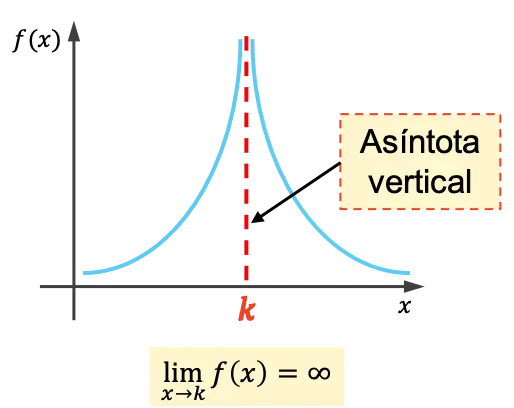
الخط المقارب الرأسي للدالة هو خط عمودي يقترب رسمه البياني إلى ما لا نهاية دون تجاوزه على الإطلاق. ولذلك، فإن معادلة الخط المقارب الرأسي هي x=k ، حيث k هي قيمة الخط المقارب الرأسي.

أي أن k هو خط مقارب عمودي إذا كانت نهاية الدالة عندما يقترب x من k لا نهائية.

كيفية حساب الخط المقارب الرأسي للدالة

لحساب الخط المقارب الرأسي للدالة، يجب اتباع الخطوات التالية:

أوجد مجال الدالة. إذا كانت جميع النقاط في المجال، فلن يكون للدالة خطوط مقاربة رأسية.
احسب نهاية الدالة عند نقاط ليست في المجال.
ستكون الخطوط المقاربة الرأسية للدالة هي جميع القيم التي يعطي فيها الحد ما لا نهاية.

لاحظ أن الدالة يمكن أن تحتوي على أكثر من خط مقارب رأسي. على سبيل المثال، الرسم البياني لدالة الظل يحتوي على عدد لا نهائي من الخطوط المقاربة الرأسية.

➤ انظر: خصائص دالة الظل

مثال على الخط المقارب العمودي

على سبيل المثال، سنجد جميع الخطوط المقاربة للدالة المنطقية التالية حتى تتمكن من رؤية كيفية القيام بذلك:

$f(x)=\cfrac{1}{x-2}$

بشكل عام، النقاط التي توجد بها خطوط مقاربة رأسية لا تنتمي إلى مجال الدالة. لذلك، سنقوم أولاً بحساب مجال الدالة.

إنها دالة عقلانية، لذلك ننظر إلى وقت اختفاء المقام لتحديد النقاط التي لا تنتمي إلى المجال:

$x-2=0$

$x=2$

وبالتالي فإن مجال الدالة هو جميع الأعداد الحقيقية باستثناء x=2:

$\text{Dom } f = \mathbb{R} - \{2\}$

لذلك يمكن أن يكون x=2 خطًا مقاربًا رأسيًا للدالة. للتحقق من ذلك، يجب علينا حساب نهاية الدالة عند هذه النقطة:

$\displaystyle \lim_{x \to 2} \frac{1}{x-2}=\frac{1}{2-2}=\frac{1}{0}=\infty$

في هذه الحالة حصلنا على عدم تعيين عدد بين الصفر، وبالتالي، لحل النهاية يجب علينا حساب الحدود الجانبية لمعرفة ما إذا كانت زائد ما لا نهاية، أو ناقص ما لا نهاية أو إذا كانت النهاية غير موجودة. ومع ذلك، عندما نحسب الخطوط المقاربة الرأسية، لا نحتاج إلى حساب النهايات الجانبية، لكن الحصول على عدم التعيين هذا يكفي للقول إنه خط مقارب رأسي.

باختصار، بما أن نهاية الدالة عندما تقترب x من 2 تعطي ما لا نهاية، فإن x=2 هو خط مقارب رأسي.

فيما يلي الوظيفة ممثلة بيانيا. كما ترون، فهو يقترب جدًا من الخط x=2 (من اليسار واليمين) ولكنه لا يتقاطع معه أبدًا لأنه خط مقارب رأسي:

بالإضافة إلى ذلك يمكننا أن نستنتج من الرسم البياني الحدود الجانبية للدالة عند النقطة x=2:

$\displaystyle \lim_{x \to 2^-} \frac{1}{x-2} = -\infty \qquad \lim_{x \to 2^+} \frac{1}{x-2} = +\infty$

حل مسائل الخطوط المقاربة العمودية

التمرين 1

احسب الخط المقارب الرأسي للدالة المنطقية التالية:

$\displaystyle f(x)=\frac{3x-1}{2x-1}$

انظر الحل

لا توجد صيغة لحساب الخطوط المقاربة الرأسية للدالة، ولكن عليك العثور على مجال الدالة ومعرفة النقاط التي لم يتم فيها تعريف الدالة، حيث يعطي الحد ما لا نهاية.

ولذلك، فإننا نجعل مقام الدالة الكسرية يساوي 0 للعثور على النقاط التي لا تنتمي إلى المجال:

$2x -1 =0$

$2x= 1$

$x = \cfrac{1}{2}$

وبالتالي فإن مجال الدالة هو جميع الأعداد الحقيقية باستثناء x=1/2:

$\text{Dom } f = \mathbb{R} - \left\{ \cfrac{1}{2} \right\}$

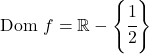
إذن x=1/2 يمكن أن يكون خطًا مقاربًا رأسيًا. للتحقق من ذلك، نحسب نهاية الدالة عند هذه النقطة:

$\displaystyle \lim_{x \to \frac{1}{2} } \cfrac{3x-1}{2x-1} = \cfrac{3\cdot\cfrac{1}{2}-1}{2\cdot\cfrac{1}{2}-1} = \cfrac{ \cfrac{3}{2} -1 }{\cfrac{2}{2} -1 } = \cfrac{ \cfrac{1}{2} }{1-1}=\cfrac{\cfrac{1}{2}}{0} =\infty$

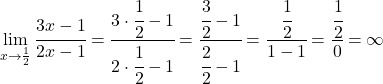
إذن x=1/2 هو خط مقارب رأسي ، لأن نهاية الدالة عند هذه النقطة تعطي ما لا نهاية.

تمرين 2

ابحث عن جميع الخطوط المقاربة الرأسية للدالة الكسرية التالية:

$\displaystyle f(x)=\frac{2x+1}{x^2-9}$

انظر الحل

أولاً، نجعل مقام الكسر يساوي صفرًا لنرى أي القيم ليست في مجال الدالة:

$x^2-9=0$

نحل المعادلة التربيعية غير الكاملة:

$x^2=9$

$x=\pm 3$

وبالتالي فإن مجال الوظيفة العقلانية هو:

$\text{Dom } f = \mathbb{R} - \left\{3, -3\right\}$

لذا، لتحديد أي من هاتين القيمتين هي خطوط مقاربة رأسية، فإننا نحل قيمة نهاية الدالة عند كل نقطة:

$\displaystyle\lim_{x \to 3}\frac{2x+1}{x^2-9}=\frac{2\cdot3+1}{3^2-9}=\frac{7}{9-9}=\frac{7}{0}=\infty$

$\displaystyle\lim_{x \to -3}\frac{2x+1}{x^2-9}=\frac{2\cdot(-3)+1}{(-3)^2-9}=\frac{-5}{9-9}=\frac{-5}{0}=\infty$

الحدان يعطيان ما لا نهاية، لذا فإن x=3 و x=-3 هما الخطان المقاربان الرأسيان لدالة المشكلة .

التمرين 3

أوجد، إذا كان لديك، جميع الخطوط المقاربة الرأسية للدالة المنطقية التالية:

$\displaystyle f(x)=\frac{x+3}{x^2+2x-3}$

➤ انظر: صفر بين صفر عدم تحديد

انظر الحل

أولاً، نقوم بحل معادلة المقام التربيعي لإيجاد القيم التي تلغي مقام الكسر:

$x^2+2x-3=0$

$\begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}$

إذن مجال الدالة هو:

$\text{Dom } f = \mathbb{R} - \left\{1, -3\right\}$

لذا، نحسب أولًا نهاية الدالة عند x=1:

$\displaystyle\lim_{x \to 1}\frac{x+3}{x^2+2x-3}=\frac{1+3}{1^2+2\cdot 1-3}=\frac{4}{0}=\infty$

ومن ناحية أخرى، نحل نهاية الدالة عندما تتجه x نحو -3:

$\begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}$

النهاية السابقة تعطي الصيغة غير المعينة صفر بين صفر، لذا لحلها نحتاج إلى تحليل كثيرات الحدود. إذا كانت لديك أي شكوك حول كيفية حل النهاية، يمكنك الاطلاع على الشرح الكامل لكيفية حل هذا النوع من عدم التعيين في الرابط الخاص ببيان التمرين.

في هذه الحالة، فقط نهاية الدالة عند النقطة x=1 هي التي تعطي ما لا نهاية، لذا فإن x=1 هو الخط المقارب الرأسي الوحيد للدالة .

ما هو الخط المقارب العمودي؟

كيفية حساب الخط المقارب الرأسي للدالة

مثال على الخط المقارب العمودي

حل مسائل الخطوط المقاربة العمودية

التمرين 1

تمرين 2

التمرين 3

اترك تعليقاً إلغاء الرد