نوضح في هذه المقالة ما هي الخطوط المقاربة الأفقية للدالة وكيفية حسابها. بالإضافة إلى ذلك، ستجد العديد من الأمثلة على هذا النوع من الخطوط المقاربة لفهم المفهوم بشكل كامل، بالإضافة إلى ذلك، ستكون قادرًا على التدرب على حل تمارين الخطوط المقاربة الأفقية.
ما هو الخط المقارب الأفقي؟
الخط المقارب الأفقي للدالة هو خط أفقي يقترب منه الرسم البياني الخاص به إلى أجل غير مسمى دون تجاوزه على الإطلاق. ولذلك، فإن معادلة الخط المقارب الأفقي هي y=k ، حيث k هي قيمة الخط المقارب الأفقي.
أي أن k هو خط مقارب أفقي إذا كانت نهاية الدالة عندما تقترب x من اللانهاية تساوي k .
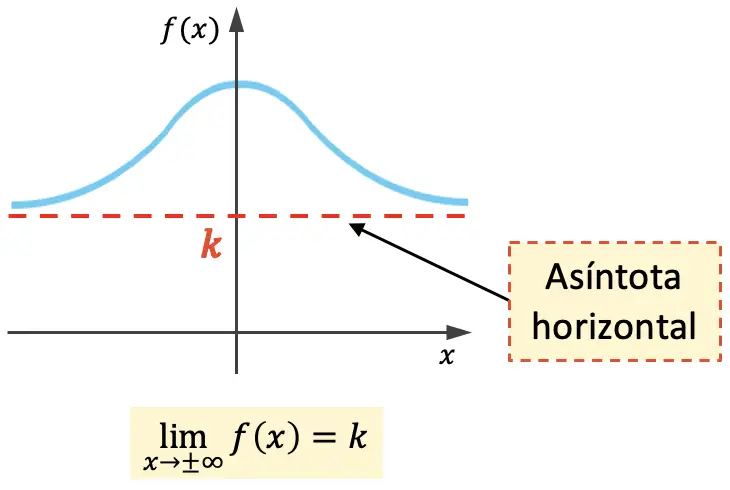
تحتوي الدالة أعلاه على خط تقارب أفقي على جانبي الرسم البياني، ولكن يمكن أن يكون للدالة خط تقارب أفقي على جانب واحد فقط:
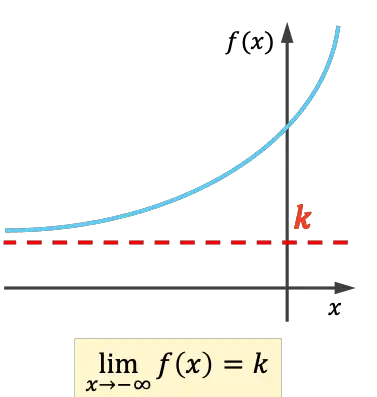
- تحتوي الدالة على خط تقارب أفقي أيسر إذا كانت النهاية إلى ما لا نهاية على الأقل تعطي عددًا حقيقيًا.
- تحتوي الدالة على خط تقارب أفقي إلى اليمين إذا كانت نهاية زائد ما لا نهاية تعطي عددًا حقيقيًا.

كيفية حساب الخط المقارب الأفقي للدالة
لحساب الخط المقارب الأفقي للدالة، يجب اتباع الخطوات التالية:
- احسب نهاية الدالة إلى اللانهاية (+∞ و-∞).
- إذا كانت نهاية اللانهاية تعطي رقمًا حقيقيًا (k)، فإن الخط y=k هو خط تقارب أفقي للدالة.
- إذا لم يكن أي من الحدين يتوافق مع عدد حقيقي، فلن يكون للدالة خطوط تقارب أفقية.
مثال الخط المقارب الأفقي
حتى تتمكن من رؤية مثال لكيفية القيام بذلك، سوف نقوم بإزالة جميع الخطوط المقاربة الأفقية من الدالة الكسرية التالية:
![]()
لتحديد الخطوط المقاربة الأفقية، من الضروري حساب النهاية عند سالب ما لا نهاية وعند زائد ما لا نهاية للدالة:
![]()
![]()
➤ انظر: كيفية حل عدم التحديد اللانهائي بين اللانهائي
الحدان عند اللانهاية يعطيان 1، لذا فإن y=1 هو الخط المقارب الأفقي الوحيد للدالة.
فيما يلي الوظيفة ممثلة بيانيا. كما ترون، فإن الدالة تقترب جدًا من y=1 (سواء عند زائد ما لا نهاية أو ناقص ما لا نهاية)، لكنها لا تلمسها أبدًا لأنها خط مقارب أفقي.

ملاحظة: في بعض الحالات الخاصة، تتقاطع الدالة مع الخط المقارب الأفقي عند نقطة واحدة أو أكثر، ولكن بشكل عام، الرسم البياني للدالة لا يتقاطع مع خطوط التقارب الخاصة به.
من ناحية أخرى، تحتوي هذه الدالة أيضًا على خط تقارب رأسي عند x=1. لأنه، كما ترون من الرسم البياني، فإنه يقترب جدًا من الخط x=1 ولكنه لا يصل إلى هذه القيمة أبدًا.
حل مسائل الخطوط المقاربة الأفقية
التمرين 1
أوجد الخط المقارب الأفقي، إن وجد، للدالة الكسرية التالية:
![]()
لتحديد الخطوط المقاربة الأفقية للدالة العقلانية، من الضروري حساب الحدود عند ما لا نهاية للدالة:
![]()
![]()
في هذه الحالة، نتيجة الصيغة غير المحددة ∞/∞ هي تقسيم معاملات x من أعلى درجة، حيث أن البسط والمقام من نفس الترتيب.
الحدود عند زائد ما لا نهاية وناقص ما لا نهاية للدالة تعطي 2، لذا فإن y=2 هو خط مقارب أفقي وهو الخط الوحيد الذي تمتلكه الدالة.
تمرين 2
أوجد جميع الخطوط المقاربة الأفقية للدالة المنطقية التالية ذات الجذر:
![]()
للعثور على الخطوط المقاربة الأفقية للدالة، نحسب أولاً النهاية عند اللانهاية الموجبة:
![]()
ثم نحل نهاية الدالة إلى ما لا نهاية سالبة:
![]()
➤ إذا كانت لديك أي شكوك حول كيفية حل حدود اللانهاية، نوصي بمراجعة الرابط أعلاه حول كيفية حل عدم التعيين اللانهائي بين اللانهاية.
في هذه الحالة، حصلنا على قيمتين مختلفتين للحدود عند ما لا نهاية. وبالتالي، تحتوي الدالة على خطين مقاربين أفقيين: y=3 هو خط تقارب أفقي للدالة على اليمين، ومن ناحية أخرى، y=-3 هو خط تقارب أفقي للدالة على اليسار.
التمرين 3
احسب الخطوط المقاربة الأفقية للدالة المحددة متعددة التعريف التالية:
![Rendered by QuickLaTeX.com \displaystyle f(x)=\left\{ \begin{array}{lcl}\displaystyle\frac{3x-1}{x^2}& \text{si} & x<4\\[4ex]\displaystyle\frac{x^3-2x+5}{2x^3-9} & \text{si} & x\geq 4 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa168db8e7d068a6d331e40401a90da6_l3.png)
لحساب الخطوط المقاربة الأفقية للدالة، لا توجد صيغة، ولكن يجب عليك حساب حدود زائد وناقص ما لا نهاية.
وبالتالي، لإيجاد النهاية اللانهائية على الأقل، نأخذ الدالة المعرفة في القسم الأول:
![]()
وبالتالي فإن الخط y=0 هو خط مقارب أفقي على يسار الدالة.
والآن نحسب النهاية عند زائد ما لا نهاية عن طريق أخذ الدالة المحددة في القسم الثاني:
![]()
وبالتالي فإن الخط y=1/2 هو خط مقارب أفقي على يمين الدالة.