▷ الخط المقارب المائل للدالة (تمارين محلولة)

نوضح في هذه المقالة ما هي الخطوط المقاربة المائلة للدالة. سوف تتعلم متى يكون للدالة خط مقارب مائل وكيفية حسابه. بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة على الخطوط المقاربة المائلة والتدرب على حل التمارين خطوة بخطوة.

ما هو الخط المقارب المائل؟

الخط المقارب المائل للدالة هو خط مائل يقترب منه الرسم البياني إلى ما لا نهاية دون تجاوزه. وبالتالي، فإن جميع الخطوط المقاربة المائلة هي خطوط معادلة y=mx+n .

يتم حساب ميل وأصل الخط المقارب المائل باستخدام الصيغ التالية:

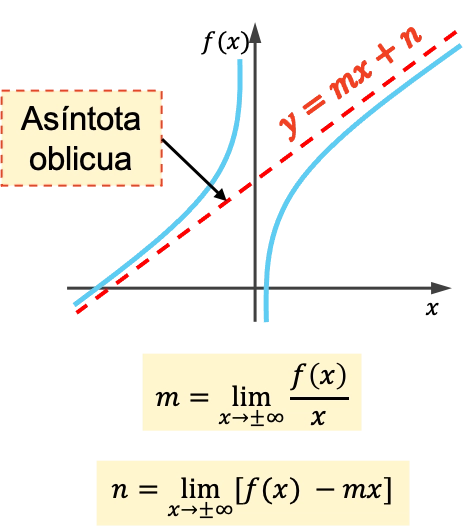
كيفية حساب الخط المقارب المائل للدالة

لحساب الخط المقارب المائل للدالة، يجب تنفيذ الخطوات التالية:

احسب نهاية ما لا نهاية للدالة مقسومة على x.
إذا كانت النهاية أعلاه تؤدي إلى رقم حقيقي غير الصفر، فهذا يعني أن الدالة لها خط تقارب مائل. علاوة على ذلك، فإن ميل الخط المقارب المائل المذكور سيكون هو القيمة التي تم الحصول عليها عند النهاية.

$\displaystyle m = \lim_{x \to \pm\infty}\frac{f(x)}{x}$

في هذه الحالة، كل ما تبقى هو حساب تقاطع الخط المقارب المائل عن طريق حل النهاية التالية:

$\displaystyle n = \lim_{x \to \pm\infty} [f(x)-mx]$

ملاحظة: يجب حساب النهايات عند زائد وناقص ما لا نهاية، لكنها عادة ما تعطي نفس النتيجة ولهذا السبب نقوم بتبسيطها بوضع ±∞. لكن إذا كانت الحدود عند زائد وناقص اللانهاية مختلفة، فيجب حساب الخط المقارب المائل الأيسر والخط المقارب المائل الأيمن بشكل منفصل.

مثال الخط المقارب

بعد ذلك، سنأخذ الخط المقارب المائل للدالة المنطقية التالية حتى تتمكن من رؤية مثال لكيفية القيام بذلك:

$f(x)=\cfrac{x^2+1}{x}$

الخطوط المقاربة المائلة هي من النوع

$y=mx+n.$

لذا، علينا أولًا حساب ميل الخط

$m$

مع الصيغة المقابلة لها:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}$

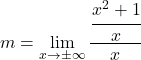
لحل هذه النهاية يجب علينا تطبيق خصائص الكسور:

$\cfrac{\cfrac{a}{b}}{\cfrac{c}{d}}=\cfrac{a\cdot d}{b\cdot c}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}=\lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2}$

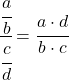
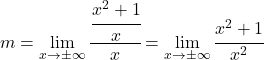
والآن نحسب الحد:

$\displaystyle m = \lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2} = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = \bm{1}$

في هذه الحالة، نتيجة عدم تحديد اللانهاية بين اللانهاية هو تقسيم معاملات x من أعلى درجة، حيث أن البسط والمقام من نفس الترتيب.

النهاية أعلاه تعطي رقمًا حقيقيًا غير الصفر، لذا فإن الدالة لها خط تقارب مائل. سنقوم الآن بحساب التقاطع y

$n$

من الخط المقارب باستخدام الصيغة المقابلة له:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right]$

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]$

نحاول حساب الحد:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

لكننا نحصل على عدم التعيين ما لا نهاية ناقص ما لا نهاية. ولذلك فمن الضروري اختزال الشروط إلى قاسم مشترك. للقيام بذلك، نضرب ونقسم x على مقام الكسر:

$\displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]$

الآن بعد أن أصبح لكلا المصطلحين نفس المقام، يمكننا تجميعهما:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}$

نحن نعمل على البسط:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}$

وأخيرًا، نحل الحد:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}= \cfrac{1}{\pm\infty} = \bm{0}$

إذن ن = 0. وبالتالي فإن الخط المقارب المائل هو دالة خطية:

$y = mx+n$

$y = 1x+0$

$\bm{y=x}$

يتم تمثيل الوظيفة المدروسة في الرسم البياني أدناه. كما ترون، فإن الدالة تقترب جدًا من الخط y=x ولكنها لا تلمسه أبدًا لأنه خط مقارب مائل:

تمارين محلولة على الخطوط المقاربة المائلة

التمرين 1

أوجد الخط المقارب المائل للدالة المنطقية التالية:

$\displaystyle f(x)= \frac{x^2+2x+3}{x+1}$

انظر الحل

الخطوط المقاربة المائلة هي من النموذج

$y=mx+n$

ولذلك فمن الضروري حساب المعلمات m و n . نحسب أولاً m بتطبيق صيغته:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+2x+3}{x+1}}{x}$

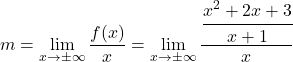
نقوم بتبسيط الكسر من خلال تطبيق خصائص الكسور:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{(x+1)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}$

ونحل الحد:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}= \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

إذن م = 1. دعونا الآن نحسب تقاطع الخط المقارب المائل من خلال تطبيق صيغته:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-1x\right]$

نحاول حساب الحد:

$\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right]= \bm{+\infty - \infty}$

لكننا نحصل على الصيغة غير المعينة ما لا نهاية ناقص ما لا نهاية. لذلك يجب علينا اختزال المصطلحات في قاسم مشترك ومن ثم تجميعها:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}$

وأخيرًا، نحل الحد:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{x+3}{x+1} = \frac{\infty}{\infty} = \frac{1}{1} = \bm{1}$

باختصار، الخط المقارب المائل للدالة هو:

$y = mx+n$

$y = 1x + 1$

$\bm{y = x + 1}$

تمرين 2

أوجد جميع الخطوط المقاربة المائلة للدالة المنطقية التالية:

$\displaystyle f(x)=\frac{2x^2-5}{x+3}$

انظر الحل

أولاً، نستخدم صيغة ميل الخط المقارب المائل:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{2x^2-5}{x+3}}{x}$

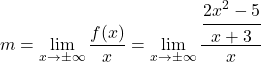
نقوم بتبسيط الكسر من خلال تطبيق خصائص الكسور:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{(x+3)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}$

ونحدد الحد:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}= \frac{+\infty}{+\infty} = \frac{2}{1} = \bm{2}$

النهاية تعطي عددًا حقيقيًا غير الصفر، لذا فهي دالة كسرية ذات خط تقارب مائل ميله 2.

الآن دعونا نحسب التقاطع من خلال تطبيق الصيغة المقابلة:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]$

نحاول حساب الحد:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]= \bm{+\infty - \infty}$

ولكننا نحصل على الفرق في عدم تحديد اللانهاية. ولذلك نختصر المصطلحات إلى قاسم مشترك ومن ثم نعمل:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}$

وأخيرًا، نحل الحد:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{-6x-5}{x+3}= \frac{\infty}{\infty}=\frac{-6}{1} = \bm{-6}$

باختصار، الخط المقارب المائل للدالة الكسرية هو:

$y = mx+n$

$\bm{y=2x-6}$

ما هو الخط المقارب المائل؟

كيفية حساب الخط المقارب المائل للدالة

مثال الخط المقارب

تمارين محلولة على الخطوط المقاربة المائلة

التمرين 1

تمرين 2

اترك تعليقاً إلغاء الرد