الحدود المثلثية -

هنا سوف تتعلم كيفية حل النهايات المثلثية. ستتمكن من رؤية العديد من الأمثلة على حدود الدوال المثلثية وحتى التدرب على حل التمارين خطوة بخطوة حول الحدود المثلثية.

ما هي الحدود المثلثية؟

الحدود المثلثية هي الحدود المحسوبة على الدوال المثلثية. لحل النهايات المثلثية، يجب تطبيق إجراء أولي، لأنها تؤدي عمومًا إلى عدم التحديد.

بالإضافة إلى ذلك، لا توجد حدود لا نهائية للدوال المثلثية، لأنها دوال دورية. أي أن رسومها البيانية تتكرر باستمرار وبشكل دوري دون الميل نحو قيمة محددة.

صيغ الحدود المثلثية

يتم حساب جميع الحدود المثلثية من الصيغتين التاليتين:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=1$

مظاهرة الصيغة

إذا حاولنا حساب النهاية بالتعويض، فسنحصل على عدم التعيين صفر بين الصفر:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=\frac{\text{sen}(0)}{0}=\frac{0}{0}$

ولكن يمكن إثبات هذه الصيغة المثلثية من خلال حساب قيم الدالة الأقرب والأقرب إلى x=0 (الزوايا بالراديان).

$\displaystyle f(x)=\frac{\text{sen}(x)}{x}=1$

$\begin{array}{c}\begin{array}{l}f(-1)=\cfrac{\text{sen}(-1)}{-1}=0,84147\\[3ex]f(-0,1)=\cfrac{\text{sen}(-0,1)}{-0,1}=0,99833\\[3ex]f(-0,01)=\cfrac{\text{sen}(-0,01)}{-0,01}=0,99998\\[3ex]f(-0,001)=\cfrac{\text{sen}(-0,001)}{-0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=1\end{array}$

$\begin{array}{c}\begin{array}{l}f(1)=\cfrac{\text{sen}(1)}{1}=0,84147\\[3ex]f(0,1)=\cfrac{\text{sen}(0,1)}{0,1}=0,99833\\[3ex]f(0,01)=\cfrac{\text{sen}(0,01)}{0,01}=0,99998\\[3ex]f(0,001)=\cfrac{\text{sen}(0,001)}{0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\end{array}$

الحدان الجانبيان للدالة المثلثية يعطيان 1، وبالتالي فإن النهاية عند النقطة x=0 هي 1:

$\begin{array}{c}\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\\[3ex]\color{orange}\bm{\downarrow}\\[2ex]\lim_{x\to 0}\displaystyle\frac{\text{sen}(x)}{x}=1\end{array}$

وبالتالي، فإن الحد المثلثي لجيب x مقسومًا على x عندما تميل x إلى 0 يساوي 1.

يمكن أيضًا تطبيق هذه الصيغة على عدة زوايا:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(kx)}{kx}=1$

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=0$

مظاهرة الصيغة

إذا حاولنا إيجاد النهاية بالتعويض المباشر، فسنحصل على الصيغة غير المعينة صفر بين صفر:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=}\frac{1-\text{cos}(0)}{0}=\frac{1-1}{0}=\frac{0}{0}$

لكن يمكننا التحقق من المساواة من الصيغة أعلاه. للقيام بذلك، يجب عليك أولاً ضرب بسط ومقام الكسر في 1 بالإضافة إلى جيب تمام x:

$\displaystyle\lim_{x\to 0}\frac{\bigl(1-\text{cos}(x)\bigr)\cdot \bigl(1+\text{cos}(x)\bigr)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

لدينا الآن هوية ملحوظة في بسط الكسر، حتى نتمكن من تبسيطه:

$\displaystyle\lim_{x\to 0}\frac{1^2-\text{cos}^2(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}^2(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

بدءًا من الهوية المثلثية الأساسية، نعيد كتابة البسط:

$\text{sen}^2(x)+\text{cos}^2(x)=1 \ \longrightarrow \ \text{sen}^2(x)=1-\text{cos}^2(x)$

$\displaystyle\lim_{x\to 0}\frac{\text{sen}^2(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

يمكننا بالتالي تحويل الكسر إلى منتج الكسور:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)\cdot \text{sen}(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{\text{sen}(x)}{1+\text{cos}(x)}$

باستخدام خصائص النهايات، يمكننا تحويل التعبير أعلاه إلى حاصل ضرب النهايات:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \lim_{x\to 0}\frac{\text{sen}(x)}{1+\text{cos}(x)}$

باستخدام الصيغة الموضحة أعلاه، يمكننا بسهولة تبسيط النهاية المثلثية:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=1$

$\displaystyle 1\cdot \lim_{x\to 0}\frac{\text{sen}(x)}{1+\text{cos}(x)}$

$\displaystyle \lim_{x\to 0}\frac{\text{sen}(x)}{1+\text{cos}(x)}$

وأخيرًا، نحسب الحد الناتج:

$\displaystyle \lim_{x\to 0}\frac{\text{sen}(0)}{1+\text{cos}(0)}=\frac{0}{1+1}=\frac{0}{2}=0$

ولذلك، يتم التحقق من صيغة النهاية المثلثية:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=0$

كما هو الحال مع الصيغة الأخرى، يمكن استخدامه أيضًا لزوايا متعددة:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(kx)}{kx}=0$

ولذلك، لحل النهايات المثلثية، يجب علينا استخدام الحساب لتحويل الدوال والحصول على تعبيرات مشابهة لهذه. بهذه الطريقة يمكننا استخدام إحدى الصيغتين وإيجاد قيمة النهاية.

من ناحية أخرى، في بعض الأحيان قد نحتاج إلى تطبيق متطابقات مثلثية معينة، لذلك نترك لك جميع الصيغ أدناه

الهويات المثلثية

الصيغة التي تربط بين النسب المثلثية الرئيسية الثلاثة:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

الهوية المثلثية الأساسية:

$\text{sen}^2(x)+\text{cos}^2(x)=1$

العلاقات المثلثية المستمدة من الأساسية:

$1+\text{tan}^2 (x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)$

$1+\text{cot}^2 (x)=\cfrac{1}{\text{sen}2(x)}=\text{cosec}^2(x)$

الزوايا المتضادة:

$\text{sen}(-x)=-\text{sen}(x)$

$\text{cos}(-x)=\text{cos}(x)$

$\text{tan}(-x)=-\text{tan}(x)$

مجموع الزاويتين:

$\text{sen}(x+y)=\text{sen}(x)\text{cos}(y)+\text{cos}(x)\text{sen}(y)$

$\text{cos}(x+y)=\text{cos}(x)\text{cos}(y)-\text{sen}(x)\text{sen}(y)$

$\text{tan}(x+y)=\cfrac{\text{tan}(x)+\text{tan}(y)}{1-\text{tan}(x)\text{tan}(y)}$

الفرق بين زاويتين:

$\text{sen}(x-y) = \text{sen}(x)\text{cos}(y)-\text{cos}(x)\text{sen}(y)$

$\text{cos}(x-y) = \text{cos}(x)\text{cos}(y)+ \text{sen}(x) sen(y)$

$\text{tan}(x-y)=\cfrac{\text{tan}(x)-\text{tan}(y)}{1+\text{tan}(x)\text{tan}(y)}$

زاوية مزدوجة:

$\text{sen}(2x) = 2\text{sen}(x)\text{cos}(x)$

$\text{cos}(2x) =\text{cos}^2(x)-\text{sen}^2(x)$

$\text{tan}(2x) =\cfrac{2\text{tan}(x)}{1-\text{tan}^2(x)}$

نصف الزاوية:

$\displaystyle \text{sen}\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1-\text{cos}(x)}{2}}$

$\displaystyle \text{cos}\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1+\text{cos}(x)}{2}}$

$\displaystyle\text{tan}\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1-\text{cos}(x)}{1+\text{cos}(x)}}$

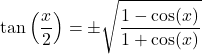
إضافة وطرح الجيب وجيب التمام:

$\displaystyle \text{sen}(x)+\text{sen}(y)=2\text{sen}\left(\frac{x+y}{2} \right)\text{cos}\left(\frac{x-y}{2} \right)$

$\displaystyle \text{sen}(x)-\text{sen}(y)=2\text{cos}\left(\frac{x+y}{2} \right)\text{sen}\left(\frac{x-y}{2} \right)$

$\displaystyle \text{cos}(x)+\text{cos}(y)=2\text{cos}\left(\frac{x+y}{2} \right)\text{cos}\left(\frac{x-y}{2} \right)$

$\displaystyle \text{cos}(x)-\text{cos}(y)=-2\text{sen}\left(\frac{x+y}{2} \right)\text{sen}\left(\frac{x-y}{2} \right)$

منتج الجيوب وجيب التمام:

$\displaystyle \text{sen}(x)\cdot \text{sen}(y)=\frac{1}{2}\Bigl[\text{cos}(x-y)-\text{cos}(x+y)\Bigr]$

$\displaystyle \text{cos}(x)\cdot \text{cos}(y)=\frac{1}{2}\Bigl[\text{cos}(x+y)+\text{cos}(x-y)\Bigr]$

$\displaystyle \text{sen}(x)\cdot \text{cos}(y)=\frac{1}{2}\Bigl[\text{sen}(x+y)+\text{sen}(x-y)\Bigr]$

لكي تتمكن من معرفة كيفية حساب الحدود المثلثية بالضبط، قمنا بتجميع مثال خطوة بخطوة أدناه.

مثال على الحد المثلثي

دعونا نرى كيف يتم حل النهاية المثلثية باستخدام المثال التالي:

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)}{x}$

وبمحاولة حساب النهاية المثلثية، نحصل على عدم تعيين صفر بين صفر:

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)}{x}=\frac{\text{tan}(0)}{0}=\frac{0}{0}$

➤ انظر: صفر حدود بين صفر

لذلك من الضروري تحويل الدالة المثلثية لحل النهاية. دالة الظل تساوي جيب التمام مقسومًا على جيب التمام، لذلك:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)}{x}=\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{x}$

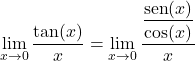
يمكننا الآن التعبير عن الدالة كحاصل الضرب من خلال تطبيق خصائص الكسور:

$\displaystyle\frac{\displaystyle\frac{a}{b}}{\displaystyle\frac{c}{d}}=\frac{a\cdot d}{b\cdot c}$

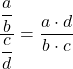
$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{\displaystyle\frac{x}{1}}=\lim_{x\to 0}{\frac{\text{sen}(x)\cdot 1}{\text{cos}(x) \cdot x}=\\[6ex]\displaystyle =\lim_{x\to 0}{\frac{\text{sen}(x)}{x\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{1}{\text{cos}(x)}\end{array}$

باستخدام خصائص النهايات، يمكننا تحويل نهاية دالتين مضروبتين إلى حاصل ضرب حدين:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\frac{1}{\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{1}{\text{cos}(x)}$

كما أظهرنا أعلاه، فإن النهاية المثلثية الأولى تعطي 1:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=1$

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{1}{\text{cos}(x)}=1\cdot\lim_{x\to 0}\frac{1}{\text{cos}(x)}=\lim_{x\to 0}\frac{1}{\text{cos}(x)}$

لذلك فقط قم بالحساب التالي:

$\displaystyle \lim_{x\to 0}\frac{1}{\text{cos}(x)}=\frac{1}{\text{cos}(0)}=\frac{1}{1}=1$

تمارين محلولة على النهايات المثلثية

التمرين 1

حل النهاية المثلثية التالية:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(4x)}{2x}$

انظر الحل

أولاً، نحاول حساب النهاية المثلثية عن طريق التقييم المباشر:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(4x)}{2x}=\frac{\text{sen}(4\cdot 0)}{2\cdot 0}=\frac{0}{0}$

لكننا نحصل على صفر على صفر من عدم التحديد. لذا علينا تطبيق التحويلات على الدالة.

أولاً، سنترك x في المقام عن طريق القيام بما يلي:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(4x)}{2x}=\lim_{x\to 0}\frac{1}{2}\cdot\frac{\text{sen}(4x)}{x}=\frac{1}{2}\cdot\lim_{x\to 0}\frac{\text{sen}(4x)}{x}$

نقوم الآن بضرب الكسر وتقسيمه على 4 للحصول على تعبير يمكن من خلاله تطبيق الصيغة الأولى للحدود المثلثية:

$\displaystyle\frac{1}{2}\lim_{x\to 0}\frac{\text{sen}(4x)\cdot 4}{x\cdot 4}=\frac{1}{2}\cdot 4 \cdot \lim_{x\to 0}\frac{\text{sen}(4x)}{4x}=2\lim_{x\to 0}\frac{\text{sen}(4x)}{4x}$

أخيرًا، نطبق الصيغة الموضحة في البداية ونحل النهاية المثلثية:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(kx)}{kx}=1$

$\displaystyle 2\lim_{x\to 0}\frac{\text{sen}(4x)}{4x}=2\cdot 1=\bm{2}$

تمرين 2

احسب النهاية المثلثية التالية:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)+\text{tan}(x)}{x}$

انظر الحل

أولًا، نحاول إيجاد النهاية المثلثية:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)+\text{tan}(x)}{x}=\frac{\text{sen}(0)+\text{tan}(0)}{0}=\frac{0}{0}$

ولكن يتم الوصول إلى الشكل غير المحدد صفر الذي يتوافق مع الصفر.

ثم نقوم بتحويل الظل إلى خارج قسمة الجيب وجيب التمام:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)+\text{tan}(x)}{x}=\lim_{x\to 0}\frac{\displaystyle\text{sen}(x)+\frac{\text{sen}(x)}{\text{cos}(x)}}{x}$

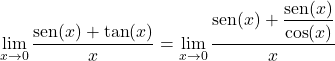
نقوم بالضرب والقسمة على جيب تمام x:

$\displaystyle\lim_{x\to 0}\frac{\left(\displaystyle\text{sen}(x)+\frac{\text{sen}(x)}{\text{cos}(x)}\right)\cdot\text{cos}(x)}{x\cdot\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)\text{cos}(x)+\text{sen}(x)}{x\cdot\text{cos}(x)}$

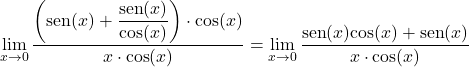
نأخذ عاملاً مشتركًا في البسط ونفصل النهاية المثلثية إلى قسمين:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)(\text{cos}(x)+1)}{x\cdot\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{\text{cos}(x)+1}{\text{cos}(x)}$

وأخيرًا، نجد نتيجة النهاية المثلثية:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{\text{cos}(x)+1}{\text{cos}(x)}=1\cdot\frac{\text{cos}(0)+1}{\text{cos}(0)} =\frac{1+1}{1}=\bm{2}$

التمرين 3

حل نهاية الدالة المثلثية التالية عندما تقترب x من الصفر:

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)-\text{sen}{(x)}}{3x\cdot\text{tan}(x)}$

انظر الحل

بإجراء الحساب المباشر نحصل على الحد غير المحدد 0 بين 0:

$\displaystyle\lim_{x\to 0}}\frac{\text{tan}(x)-\text{sen}(x)}{3x\cdot\text{tan}(x)}=\frac{\text{tan}(0)-\text{sen}(0)}{3\cdot 0\cdot\text{tan}(0)}=\frac{0}{0}$

ومن ثم، فإننا سوف نبسط النهاية بقسمة كل حد على ظل x:

$\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{tan}(x)}{\text{tan}(x)}-\frac{\text{sen}(x)}{\text{tan}(x)}}{\displaystyle\frac{3x\cdot\text{tan}(x)}{\text{tan}(x)}}=\lim_{x\to 0}\frac{\displaystyle 1-\frac{\text{sen}(x)}{\text{tan}(x)}}{3x}$

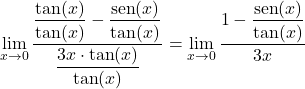
ثانيًا، يمكننا أن نستنتج من الهوية المثلثية الأساسية أن كسر البسط يعادل جيب تمام x:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}\ \longrightarrow \ \text{cos}(x)=\cfrac{\text{sen}(x)}{\text{tan}(x)}$

$\displaystyle\lim_{x\to 0}\frac{\displaystyle 1-\frac{\text{sen}(x)}{\text{tan}(x)}}{3x}=\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}$

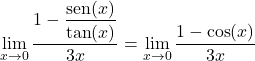
وبتطبيق الصيغة الثانية الموضحة في نظرية النهايات المثلثية يمكننا بسهولة حل النهاية:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=0$

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}=\lim_{x\to 0}\frac{1}{3}\cdot \frac{1-\text{cos}(x)}{x}=\\[4ex]\displaystyle =\frac{1}{3}\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=\frac{1}{3}\cdot 0=\bm{0}\end{array}$

التمرين 4

أوجد حل النهاية المثلثية التالية عند النقطة x=0:

$\displaystyle\lim_{x\to 0}\frac{2\text{sen}(x)\text{cos}(x)\text{sen}(5x)}{x^2}$

انظر الحل

إذا حاولنا حل النهاية، نجد الصيغة غير المحددة 0/0:

$\displaystyle\lim_{x\to 0}\frac{2\text{sen}(x)\text{cos}(x)\text{sen}(5x)}{x^2}=\frac{2\text{sen}(0)\text{cos}(0)\text{sen}(5\cdot 0)}{0^2}=\frac{0}{0}$

يمكن إعادة كتابة التعبير الجبري للبسط باستخدام الهوية المثلثية لجيب الزاوية المزدوجة:

$\text{sen}(2x)=2\text{sen}(x)\text{cos}(x)$

$\displaystyle\lim_{x\to 0}\frac{2\text{sen}(x)\text{cos}(x)\text{sen}(5x)}{x^2}=\lim_{x\to 0}\frac{\text{sen}(2x)\text{sen}(5x)}{x^2}$

الآن دعونا نفصل نهاية الدالة المثلثية إلى منتج:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)\cdot \text{sen}(5x)}{x\cdot x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}\end{array}$

وأخيرًا، نحل النهاية المثلثية من خلال تطبيق خصائص النهايات:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =2\cdot \lim_{x\to 0}\frac{\text{sen}(2x)}{2x}\cdot 5\cdot \lim_{x\to 0}\frac{\text{sen}(5x)}{5x}=\\[4ex]\displaystyle =2\cdot 1\cdot 5\cdot 1=\bm{10}\end{array}$

ما هي الحدود المثلثية؟

صيغ الحدود المثلثية

مثال على الحد المثلثي

تمارين محلولة على النهايات المثلثية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد