كيفية حساب جمع المصفوفات والطرح

في هذه الصفحة سنرى كيفية جمع وطرح المصفوفات . لديك أيضًا أمثلة ستساعدك على فهم الأمر بشكل مثالي وحل التمارين حتى تتمكن من التدرب عليها. سوف تجد أيضًا جميع خصائص إضافة المصفوفة.

كيفية إضافة وطرح المصفوفات؟

لحساب جمع (أو طرح) مصفوفتين، يجب عليك إضافة (أو طرح) العناصر التي تشغل نفس الموضع في المصفوفات.

أمثلة:

أمثلة على الجمع والطرح في المصفوفات 2×2، والعمليات على المصفوفات

لاحظ أنه لإضافة أو طرح مصفوفتين، يجب أن يكون لهما نفس البعد. على سبيل المثال، لا يمكن إضافة المصفوفات التالية لأن الأولى مصفوفة 2×2 والثانية مصفوفة 3×2:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}

حل تمارين جمع وطرح المصفوفات

التمرين 1

احسب المجموع التالي لمصفوفات 2×2:

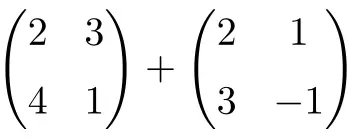
تم حل التمرين خطوة بخطوة لإضافة مصفوفات 2x2

وهي عبارة عن مجموع مصفوفتين مربعتين أبعادهما 2×2:

\displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}

تمرين 2

قم بإجراء عملية طرح المصفوفة التالية:

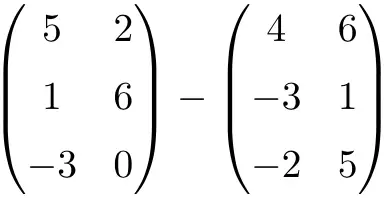
تمرين تم حله خطوة بخطوة في المصفوفات، العمليات على المصفوفات

وهو طرح مصفوفتين البعد 3×2:

\displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}

التمرين 3

أوجد نتيجة مجموع المصفوفة التالية للبعد 3×3:

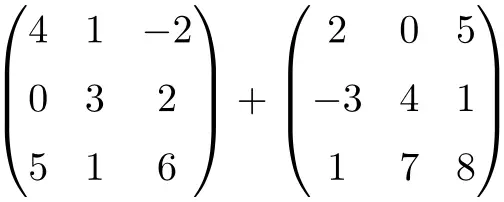
تمرين تم حله خطوة بخطوة في جمع المصفوفات 3×3، والعمليات على المصفوفات

وهي عبارة عن مجموع مصفوفتين مربعتين من الرتبة 3×3:

\displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}

التمرين 4

احسب الجمع والطرح التالي للمصفوفات المربعة من الرتبة 2:

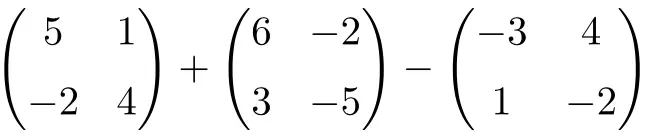
تمرين تم حله خطوة بخطوة، الجمع والطرح لمصفوفات 2×2، والعمليات على المصفوفات

إنها عملية مقترنة بالجمع والطرح للمصفوفات المربعة من الرتبة 2:

\displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

لذا، نقوم أولاً بإضافة المصفوفات الموجودة على اليسار:

\displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

ثم نحسب طرح المصفوفات:

\displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}

التمرين 5

حل مصفوفة الجمع والطرح التالية:

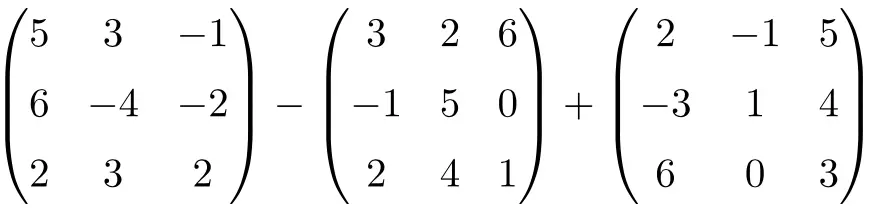
تمرين تم حله خطوة بخطوة، الجمع والطرح للمصفوفات 3×3، والعمليات على المصفوفات

إنها عملية مشتركة للطرح والجمع للمصفوفات المربعة من الرتبة 3:

\displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

أولاً، نحل عملية طرح المصفوفات:

\displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

وأخيرا نضيف المصفوفات:

\displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}

الآن بعد أن عرفت كيفية جمع المصفوفات وطرحها، فقد حان الوقت لمعرفة كيفية ضرب المصفوفات ، وهي بالتأكيد أهم عمليات المصفوفات. ستجد أيضًا تمارين حل المصفوفات خطوة بخطوة بحيث يمكنك التدرب عليها، كما هو الحال في جميع صفحات هذا الموقع. 😉

إضافة خصائص المصفوفة

تتميز إضافة المصفوفة بالخصائص التالية:

  • إضافة المصفوفة لها الخاصية التبادلية :

\displaystyle A +B = B + A

وبالتالي، فإن الترتيب الذي نضيف به المصفوفات هو نفسه. لتوضيح ذلك، سوف نقوم بإضافة مصفوفتين عن طريق تغيير ترتيبهما وسترى كيف أن النتيجة هي نفسها.

لذلك ننتقل إلى إضافة مصفوفتين بترتيب معين:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

لاحظ أنه إذا عكسنا ترتيب جمع المصفوفات، تبقى النتيجة كما هي:

\displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

  • خاصية أخرى لجمع المصفوفات هي خاصية العنصر المقابل:

\displaystyle A + (-A) =0

بمعنى آخر، إذا أضفنا مصفوفة بالإضافة إلى نفس المصفوفة ولكن مع تغير جميع عناصرها، ستكون النتيجة مصفوفة صفرية:

\displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}

  • تحتوي إضافة المصفوفة أيضًا على خاصية العنصر المحايد:

\displaystyle A + 0 =A

هذه الخاصية هي الأكثر وضوحًا، فهي تشير إلى أن أي مصفوفة بالإضافة إلى مصفوفة مليئة بالأصفار تعادل نفس المصفوفة:

\displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}

  • إضافة المصفوفة لها الخاصية الترابطية:

\displaystyle\left( A + B \right) + C =A + \left( B + C \right)

ومن ثم، فإن الترتيب الذي نضيف به المصفوفات هو نفسه. انظر إلى المثال التالي، حيث جمعنا 3 مصفوفات بترتيب مختلف وكانت النتيجة واحدة:

\displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}

\begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}

\begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top