التدوين الرياضي هو وسيلة لتوصيل الأفكار والحسابات من خلال استخدام الرموز. على الرغم من أن الأمر قد يبدو مربكًا للوهلة الأولى، إلا أنه مع القليل من الممارسة ستتمكن من تفسيره بسهولة. سنوضح لك في هذه المقالة معنى جميع الرموز المستخدمة في هذا التدوين وبعض الأمثلة على كيفية تطبيقها.
ما هو التدوين الرياضي؟
التدوين الرياضي هو وسيلة لكتابة القيم والتعبيرات المستخدمة في الرياضيات. تتيح هذه التقنية لعلماء الرياضيات طرح الأفكار بإيجاز ودقة . يسمح تدوين الرياضيات أيضًا لأولئك الذين يمارسون الرياضيات أو يدرسونها بفهم المفاهيم بشكل أفضل.
لا ينبغي الخلط بين لغة الرياضيات والترميز العلمي، وهو وسيلة لكتابة القيم العددية. وفي الوقت نفسه، فإن التدوين الرياضي هو عبارة عن مجموعة من الرموز التي تسمح لك بكتابة تعبيرات معقدة، تمامًا مثل اللغة. وسنعود لهذا الموضوع بمزيد من التفصيل لاحقا.
كيف تقرأ التدوين الرياضي؟
يعد تعلم تفسير التدوين الرياضي أسهل مما يبدو، كل ما عليك فعله هو معرفة معنى كل رمز وبمجرد القيام بذلك، ستتمكن من قراءة أي شيء مكتوب بالتدوين الرياضي. الأمر بهذه البساطة، على الرغم من أنه يتطلب بوضوح الممارسة والكثير من وقت الدراسة.
التعبيرات الرياضية منطقية للغاية وتتبع الأنماط دائمًا، لذلك تحتاج فقط إلى حفظ القواعد ومن ثم ستعرف كيفية استقراءها في أي موقف. يمكننا حتى وصف حسابات معقدة للغاية، وهذا هو سحر اللغة الرياضية، الذي يسمح بتوصيل رسائل معقدة للغاية بطريقة منهجية.
مكونات التدوين الرياضي
يتكون التدوين الرياضي من سلسلة من الرموز التي تمثل الأرقام والعمليات والعلاقات بينها. قد تبدو هذه الرموز معقدة في البداية، ولكن مع القليل من الممارسة والفهم، يجب أن يصبح تفسير الرموز الرياضية أمرًا سهلاً.
وبعد ذلك، سنشرح بالتفصيل الأنواع الأربعة من العناصر التي يمكن العثور عليها في اللغة الرياضية. بدءًا من الأكثر أساسية وانتهاءً بالأكثر تعقيدًا وتجريدًا. وبمجرد الانتهاء من الشرح النظري سنتحدث عن أنواع الرموز العددية الموجودة.
الأرقام ومجموعات الأرقام
بداية يجب علينا تعريف الأعداد الرياضية ، فهي مفهوم رياضي يشير إلى كمية مرتبطة بوحدة ما. يمكننا وصف أي قيمة عددية، باتباع نظام الترقيم العشري والجمع بين الرموز التالية: 0، 1، 2، 3، 4، 5، 6، 7، 8 و9.
إذا قمنا بترتيب الأرقام وفقًا لخصائص مختلفة، فسنحصل على عدة فئات من الأرقام، تسمى مجموعات الأرقام. ولمجموعات القيم هذه أيضًا رموزها الخاصة التي تحددها، وفي القائمة التالية نعرضها جميعًا مع اسم المجموعة المقابلة:
- ℙ: الأعداد الأولية
- ℕ: الأعداد الطبيعية
- ℤ: كامل
- ℚ: الأعداد النسبية
- ℝ: الأعداد الحقيقية
- 𝕀: الأعداد الخيالية
- ℂ:الأعداد المركبة
- ℍ: الرباعيات
تُستخدم هذه الرموز عمومًا في حساباتنا لتحديد نطاق واسع من الأرقام، دفعة واحدة. على سبيل المثال، إذا كان لدينا تعبير يقبل العديد من القيم وفقا لذلك، بدلا من كتابة الأرقام واحدة تلو الأخرى، سيكون من الأسهل علينا تحديد هذه القيم من خلال الرمز المقابل لمجموعتها الرقمية .
المشغلين ومحددي الكمية
الآن بعد أن ناقشنا الأعداد، التي هي جوهر الرياضيات، نحتاج إلى الحديث عن العوامل والمحددات الكمية . الأول هو كل تلك الرموز التي تسمح لنا بتمثيل العملية: الجمع (+)، الطرح (-)، الضرب (x أو ·)، القسمة (÷)، من بين أمور أخرى.
ومع ذلك، لدينا أيضًا نوعان آخران من العوامل، وهما العوامل المنطقية والعوامل العلائقية. فالأول يعبر عن الوصل والانفصال والنفي. إنها تساعدنا على اقتراح العمليات المنطقية ، والتي، على عكس العمليات الحسابية، لا تعمل مع الأرقام، ولكن مع المقترحات الرياضية.
بينما يتيح لنا الثاني إنشاء معادلات وعلاقات بين القيم أو التعبيرات الرياضية. يمكن استخدام هذه الرموز في العمليات الحسابية (لترتيب الأعداد)، لكنها أكثر أهمية في الجبر، عندما يكون لدينا متغيرات (المزيد حول هذا في قسمين).
في القائمة التالية يمكنك العثور على تعريف لجميع العوامل التي ناقشناها حتى الآن:
| رمز | تعريف | عطوف |
| + | إضافة | العامل الحسابي |
| – | الطرح | العامل الحسابي |
| ×، *، · | عمليه الضرب | العامل الحسابي |
| ÷ | قسم | العامل الحسابي |
| ײ | التمكين | العامل الحسابي |
| √ | إيداع | العامل الحسابي |
| و | اِقتِران | عامل منطقي |
| أيضاً | انفصال | عامل منطقي |
| لا | إنكار | عامل منطقي |
| = | يساوي | عامل العلاقة |
| > | أكبر من | عامل العلاقة |
| < | اصغر من | عامل العلاقة |
| >= | أفضل من أو يساوي | عامل العلاقة |
| <= | اقل او يساوي | عامل العلاقة |
| ≠ | لا يساوي | عامل العلاقة |
| ≡ | بالضبط نفس الشيء | عامل العلاقة |
| ≈ | متساوية تقريبا | عامل العلاقة |
| ≃ | أي ما يعادل | عامل العلاقة |
| ∝ | متناسب | عامل العلاقة |
على الرغم من وجود خمسة عوامل منطقية أخرى، والتي تستخدم لشرح المنطق الرياضي من نظرية المجموعات. وهو فرع يطبق المنطق المحدد والذي يستخدم في الحساب والهندسة والإحصاء… ثم نعرض لك الرموز المستخدمة وتعريفها.
| رمز | تعريف |
| س ∈ أ | x ينتمي إلى A |
| س ∉ أ | x لا ينتمي إلى A |
| ∪ | اتحاد |
| ∩ | تداخل |
| ⊂ | تضمين |
أما محددات الكمية فيمكن تعريفها على أنها رموز تشير إلى عدد عناصر المجموعة التي تحقق شرطًا معينًا (التكافؤ، الترتيب، العضوية، إلخ). هناك مجموعة كبيرة ومتنوعة من عوامل التشغيل، ولكن من بين أكثرها استخدامًا يمكننا تسليط الضوء على:
| رمز | تعريف | عطوف |
| ∀x | للجميع س | تحديد الكمية |
| ∃س | يوجد على الأقل x واحد | تحديد الكمية |
| ∄س | لا يوجد س | تحديد الكمية |
| ∃!س | لا يوجد سوى x واحد | تحديد الكمية |
| | | مثل | تحديد الكمية |
| ∴ | لذا | تحديد الكمية |
التعابير الرياضية وعلاقاتها
باستخدام الرموز التي تناولناها حتى الآن، يمكنك فهم الكثير من الرياضيات، لكننا لم نشرح بعد تطبيقاتها أو علاقاتها في التعبيرات المعقدة، مثل العمليات المجمعة أو العمليات الحسابية الجبرية. بالإضافة إلى ذلك، لا تزال هناك رموز علاقة يجب مناقشتها. وهؤلاء هم الذين سنراهم في هذا القسم.
بدءًا من رموز التجميع، فهي عبارة عن أقواس، وأقواس مربعة، وأقواس متعرجة. هذه العناصر ضرورية في تعيين الصيغ المعقدة. وتتمثل وظيفتها الرئيسية في إعطاء الأولوية لبعض الحسابات، ضمن تعبير عالمي. وهناك مستويات أولوية مختلفة بين الأنواع الثلاثة. في هذا التعبير يمكنك رؤية ترتيب الكتابة 3 {[2 + (3 – 2) · 2] – 4}.
| حرف او رمز | تعريف | أولوية |
| “(“و”)” | أقواس | الأولوية القصوى |
| “[“و”]” | اقواس | الأولوية الثانية |
| “{” و “}” | مفاتيح | الأولوية الثالثة |
ولإنهاء هذه الفئة، سنتحدث عن الجمع (Σ) وحاصل الضرب (∏) ، وهي عناصر تسمح لنا بوصف عمليات الجمع والضرب المتكررة. الجمع يعادل القول: “مجموع Xi، حيث أقوم بأخذ القيم من 1 إلى an”. وحاصل الضرب هو نفسه، ولكن بدلًا من الجمع، فإننا نضرب.
التحليل الجبري
أول شيء يجب مناقشته حول الرموز الجبرية هو المتغيرات، والتي يتم تمثيلها بالحروف الأبجدية. وظيفتها هي تقليد رقم ، لكن ليس لها قيمة ثابتة مثل الثوابت الرياضية ، لذا يمكنها أن تأخذ قيمًا جديدة. ينطبق هذا على المعادلات والنهايات والمشتقات والتكاملات والمصفوفات…
وأخيرًا، نريد أن نتحدث عن تمثيلات كل هذه العمليات الجبرية التي تحدثنا عنها للتو في هذه الفقرة الأخيرة. ومنذ ذلك الحين، أصبحت هذه العناصر هي أساس الجبر، وعليك أن تعرف ما هو رمزها. وبعد ذلك نعرض لكم جدولاً برموزه المختلفة وتعريف مختصر:
| رمز | تعريف |
| ليم س → ب | الحد (عندما يميل x نحو b) |
| ص ‘، ƒ’ (خ)، دى / دكس | المشتق |
| ∫ | مكتمل |
| الى ماكسن | مصفوفة الأبعاد mxn |
استنتاج بشأن رموز اللغة الرياضية
لقد رأيت حتى الآن جميع الرموز المهمة التي تغطيها الرياضيات، ومن الواضح أن هناك المزيد مما يجب مناقشته. لكن هذه أكثر تحديدًا لكل فئة فرعية من الرياضيات: الهندسة والإحصاء والجبر… لذلك سنغلق هذا الموضوع ونتحدث عن الرموز الرقمية.
أنواع الرموز العددية
سنرى في هذا القسم جميع الطرق للتعبير عن الأرقام الرياضية، حيث توجد رموز مختلفة للقيام بذلك. في البداية ذكرنا أعلاه نظام الأعداد العشرية، وهو الأكثر استخدامًا من قبل علماء الرياضيات. بعد ذلك، سنشرح ذلك بمزيد من التفصيل ونعرض لك أنواعًا أخرى من الرموز الرياضية:
العشري
نظام الأرقام العشرية هو نظام أرقام موضعية (نظام يحدد فيه موضع كل رقم قيمته) يعتمد على مضاعفات الرقم 10 ومضاعفاته الفرعية. نظرًا لأن الرقم 10 هو الرقم المستخدم كقاعدة رقمية . ولذلك فإن رموز الأرقام العشرة التي سنستخدمها هي: 1، 2، 3، 4، 5، 6، 7، 8، 9 و0.
يتم تحديد قيمة هذه الأرقام من مجموع الأرقام مضروبة في القوى في الأساس العشرة، والتي يتم تحديدها وفقًا للموضع . ومن المهم جدًا أن تتذكر أنه لكتابة رقم أقل من واحد، يجب عليك استخدام العلامة العشرية. فيما يلي مثال:
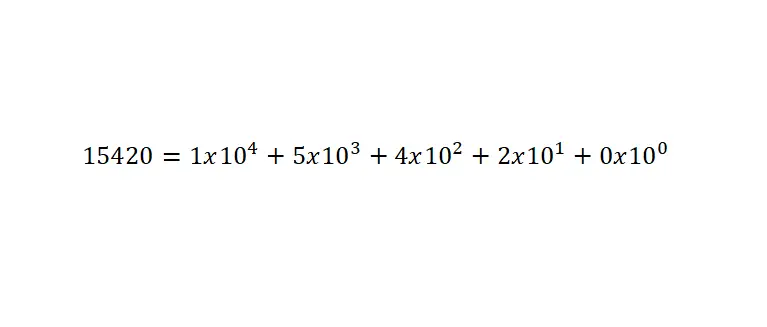
الترميز العلمي
من الواضح أن التدوين الأسي أو التدوين العلمي هو أحد أكثر أنواع الكتابة استخدامًا في العلوم والتكنولوجيا. في الواقع، هذا يسمح لنا بالتعبير عن الأعداد الكبيرة جدًا والصغيرة جدًا بطريقة بسيطة. لفهم تعريف الترميز العلمي، سنشرح كيفية تمرير عدد صحيح إلى هذا الترميز:
- تحريك العلامة العشرية: يجب عليك تحريك العلامة العشرية عدة مرات حسب الضرورة حتى تصل إلى الرقم الأول (إلى اليسار إذا كان لديك رقم كبير جدًا وإلى اليمين إذا كان لديك رقم صغير جدًا).
- إنشاء القاعدة: اكتب هذا الرقم الأخير مضروبًا في عشرة، لذا، بجانب القيمة التي حصلت عليها عن طريق تحريك العلامة العشرية إلى جانب واحد، يجب عليك كتابة الضرب في عشرة: “× 10”.
- أضف أسًا: بقيمة تساوي عدد المرات التي قمت فيها بتحريك العلامة العشرية. مع الأعداد الكبيرة، ستترك الأس موجبًا، لكن مع الأعداد الصغيرة، يجب أن تكتبه بعلامة سالبة.
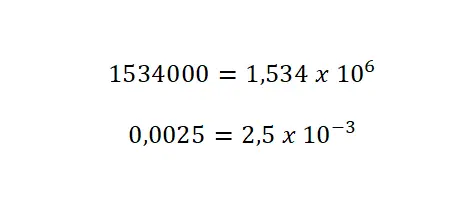
تدوين سداسي عشري
يعتمد النظام السداسي العشري على الرقم 16، مما يعني أنه يستخدم ستة عشر رمزًا مختلفًا: 0، 1، 2، 3، 4، 5، 6، 7، 8، 9، A، B، C، D، E، وF كما يمكنك. انظر، يتكون نظام الترقيم هذا من أرقام النظام العشري وستة أحرف. يستخدم هذا الترميز بشكل عام بشكل خاص في مجال تكنولوجيا المعلومات وكل ما يتعلق بتكنولوجيا المعلومات.
من المهم توضيح أنه نظرًا لوجود رموز مشتركة مع أنواع أخرى من التدوين، فيجب أن نشير دائمًا إلى أنه مكتوب بالنظام الست عشري عن طريق قوسين وفهرس 16 . في المثال التالي يمكنك أن ترى من مثال واضح جدًا تحويل الرقم السداسي العشري إلى تدوين عشري:
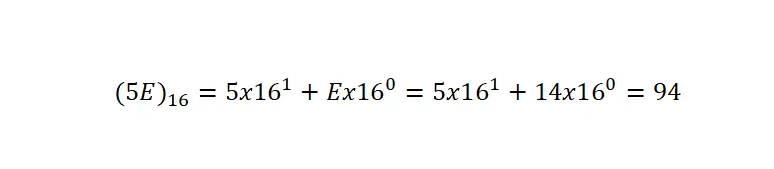
لتحويل رقم سداسي عشري إلى تعبير عشري، نحتاج إلى تقسيم الرقم إلى مضاعفاته الأساسية، كما فعلنا في التدوين العشري، ولكن تغيير الأساس إلى 16 . بعد ذلك، سنضرب كل رقم في ١٦ مرفوعًا إلى الموضع الذي يشغله هذا الرقم المحدد سالب واحد.
تدوين ثماني
النظام الأخير الذي سنتحدث عنه هو الترميز الثماني ، والذي أساسه 8. وهذا يعني أنه يستخدم ثمانية رموز أو أرقام فقط: 0، 1، 2، 3، 4، 5، 6، و7. وهو الأقل استخدامًا نظام الترقيم لجميع تلك التي شرحناها. تجدر الإشارة إلى أن تحويلات هذا الترميز تتم بنفس الإجراء المتبع في التحويلات السابقة.
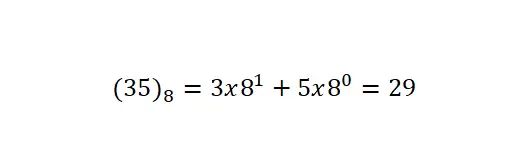
تدوين رواية
وأخيرا، يمكننا أن نتحدث عن نظام الأرقام الرومانية ، الذي لا يستخدم على نطاق واسع اليوم، ولكنه في الماضي كان مهما جدا في مجال الرياضيات. لأنه كان أحد الرموز التي جلبت الحياة إلى الرياضيات.
تقتصر كتابتك على 7 رموز: I (1)، V (5)، X (10)، L (50)، C (100)، D (500)، M (1000). وبدمج هذه الحروف تتم كتابة جميع الأرقام. إذا كنت تريد معرفة كيفية دمجها لتؤدي إلى ظهور أرقام أخرى أكبر، فننصحك بقراءة مقالتنا عنها، وذلك من خلال الرابط الأخير.
كيفية تحسين أداء القراءة في التدوين الرياضي؟
هناك عدة طرق لتحسين الأداء في قراءة التدوين الرياضي. إحدى الطرق هي قراءة الرموز والأرقام بصوت عالٍ. هناك طريقة أخرى وهي التعرف على الرموز ومعناها. يمكنك أيضًا التدرب على قراءة الرموز الرياضية باستخدام التمارين والمسائل.
نأمل أن نكون قد ساعدناك في هذا الدليل، من فضلك، إذا كان لديك أي أسئلة، فلا تتردد في كتابتها في التعليقات . أو إذا كنت ترغب في المساهمة في الموضوع، نأمل أن نرى ذلك في التعليقات أيضًا. ومع ذلك، نترك لك مقالًا عن كيفية تعلم الرياضيات ، في حال كنت ترغب في مواصلة القراءة.