▷ كيفية القيام بتحليل متعدد الحدود لرقم ✅

في هذه الصفحة، نشرح كيفية القيام بتحليل (أو تعبير) كثير الحدود لرقم. هنا يمكنك أن ترى أمثلة على تحليل كثيرات الحدود، بالإضافة إلى ذلك، ستجد تمارين محلولة خطوة بخطوة للتدرب عليها.

ما هو التحلل متعدد الحدود لعدد؟

في الرياضيات، يتكون تحليل متعدد الحدود لعدد من الأرقام من التعبير عن هذا الرقم في مجموع، بحيث يكون كل حد من المجموع هو حاصل ضرب كل رقم من الرقم بقوة الأساس 10.

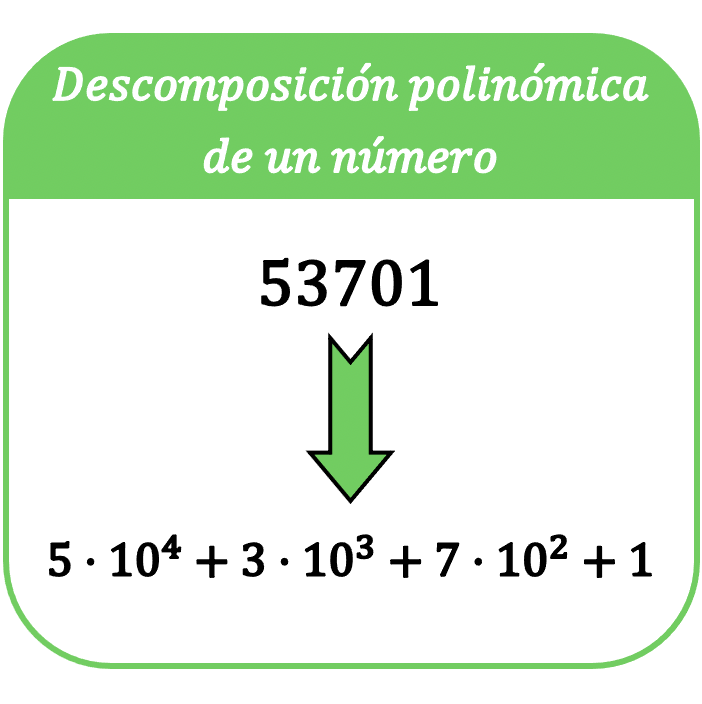
يُعرف مصطلح تحليل كثير الحدود للرقم أيضًا بالتعبير متعدد الحدود للرقم .

كيفية القيام بتحليل كثير الحدود

لإجراء تحليل متعدد الحدود لرقم ما، يجب عليك ضرب كل رقم من الرقم في 10 مرفوعًا إلى عدد الأرقام الموجودة على اليمين .

على سبيل المثال، إذا أردنا حساب تحليل كثير الحدود للرقم التالي:

$86293$

في هذه الحالة، يحتل الرقم 8 المركز الخامس، بحيث يكون على يمينه 4 أرقام. لذلك يجب علينا ضرب ثمانية في عشرة أس أربعة:

$8\cdot 10^4$

وبالتالي، لتحليل الرقم 86293 متعدد الحدود، يجب عليك أن تفعل الشيء نفسه مع جميع أرقام الرقم، والتعبير عن جميع الضربات في شكل مجموع:

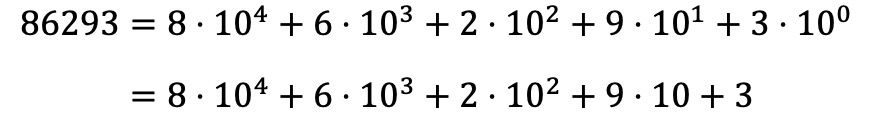
لاحظ أن الأس 10 ⁰ يختفي لأنه، وفقًا لخصائص الأس، أي رقم مرفوع إلى 0 يساوي 1، وبالتالي 10 ⁰ = 1.

من ناحية أخرى، يمكنك أيضًا العثور على تحليل كثير الحدود لعدد ما من تحليله المضاعف:

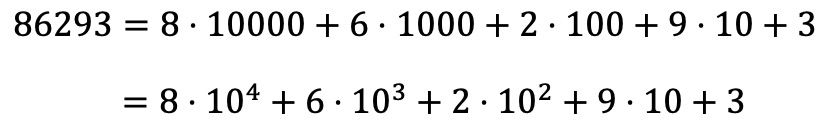
تحليل متعدد الحدود للأعداد الطبيعية للمدرسة الابتدائية

أمثلة على التحلل متعدد الحدود للأرقام

بمجرد أن رأينا كيف يتم تنفيذ تحليل كثيرات الحدود لعدد ما، سنرى أمثلة مختلفة لهذا النوع من العمليات لفهم المفهوم بشكل كامل.

تحليل متعدد الحدود لـ 3641:

$3641 = 3\cdot 10^3 +6 \cdot 10^2 + 4\cdot 10 + 1$

تحليل كثير الحدود للرقم 56912:

$56912 = 5\cdot 10^4 +6\cdot 10^3 +9 \cdot 10^2 + 1\cdot 10 + 2$

تحلل كثير الحدود لـ 27084:

$\begin{aligned} 27084 &= 2\cdot 10^4 +7\cdot 10^3 +0\cdot 10^2 + 8\cdot 10 + 4 \\[2ex] & = 2\cdot 10^4 +7\cdot 10^3 + 8\cdot 10 + 4 \end{aligned}$

في هذا المثال الأخير، يمكننا تبسيط الضرب الثالث حيث أن أي عدد مضروب في صفر يلغي.

تحليل متعدد الحدود للأعداد العشرية

لقد رأينا للتو كيفية إجراء التحليل متعدد الحدود للأعداد الطبيعية. لكن… كيف يمكنك تحليل الرقم العشري متعدد الحدود؟

حسنًا، يتم تحليل كثيرات الحدود مع الأعداد العشرية بنفس الطريقة كما هو الحال مع الأعداد الصحيحة، ولكن بالإضافة إلى ذلك، فإننا نضيف حاصل ضرب كل رقم عشري مضروبًا في قوة الأساس 10 التي يكون أسها هو الموضع العشري الذي يشغله الرقم المذكور مع قيمة سالبة لافتة.

قد يبدو هذا الأمر معقدًا جدًا عند شرحه بالكلمات، ولكن سترى أنه من خلال المثال يمكن فهمه بشكل أفضل:

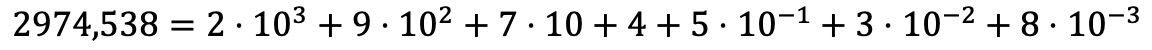
حل تمارين تحليل كثيرات الحدود

لكي تتمكن من التدرب على تحليل كثيرات الحدود، قمنا بإعداد العديد من التمارين التي تم حلها خطوة بخطوة.

لا تنس أنه يمكنك طرح أي أسئلة لديك في التعليقات! 🤔🤔🤔

التمرين 1

قم بإجراء تحليل متعدد الحدود للأرقام التالية:

$\text{A)} \ 7935$

$\text{B)} \ 1548$

$\text{C)} \ 55476$

$\text{D)} \ 287694$

انظر الحل

للعثور على تحليل كثيرات الحدود لأي رقم، اضرب كل رقم من هذا الرقم في 10 في عدد الأرقام الموجودة على اليمين، ثم قم بإضافة جميع الضربات. حتى الآن:

$\text{A)} \ 7935 = 7 \cdot 10^3+ 9\cdot 10^2 +3 \cdot 10 +5$

$\text{B)} \ 1548 = 1 \cdot 10^3+ 5\cdot 10^2 +4 \cdot 10 +8$

$\text{C)} \ 55476 = 5\cdot 10^4+ 5 \cdot 10^3+ 4\cdot 10^2 +7\cdot 10 +6$

$\text{D)} \ 287694 = 2\cdot 10^5+8\cdot 10^4+ 7 \cdot 10^3+ 6\cdot 10^2 +9\cdot 10 +4$

تمرين 2

أوجد تحليل كثيرات الحدود للأعداد التالية:

$\text{A)} \ 461$

$\text{B)} \ 3030$

$\text{C)} \ 11950$

$\text{D)} \ 8741866$

انظر الحل

لتحليل رقم متعدد الحدود، يجب عليك ضرب كل رقم من الرقم المذكور في عشرة بعدد الأرقام التي على يمينه، ثم إضافة جميع النواتج. حتى الآن:

$\text{A)} \ 461 = 4\cdot 10^2 +6 \cdot 10 +1$

$\text{B)} \ \begin{aligned} 3030 & = 3 \cdot 10^3+ 0\cdot 10^2 +3 \cdot 10 +0 \\[2ex] &= 3 \cdot 10^3+3 \cdot 10 \end{aligned}$

$\text{C)} \ 11950 = 1\cdot 10^4+ 1 \cdot 10^3+ 9\cdot 10^2 +5\cdot 10$

$\text{D)} \ 8741866 = 8\cdot 10^6+7\cdot 10^5+4\cdot 10^4+ 1 \cdot 10^3+ 8\cdot 10^2 +6\cdot 10 +6$

التمرين 3

احسب التحلل متعدد الحدود للأعداد العشرية التالية:

$\text{A)} \ 51,63$

$\text{B)} \ 249,99$

$\text{C)} \ 0,82694$

$\text{D)} \ 5,7201$

انظر الحل

في هذه المشكلة، جميع الأرقام عشرية، لذا لتحليلها يجب عليك ضرب كل رقم غير عشري في 10 مرفوعًا إلى عدد الأرقام التي يحتوي عليها حتى العلامة العشرية، وضرب كل رقم عشري في 10 مرفوعًا إلى موضعه العشري باستخدام علامة سلبية.

$\text{A)} \ 51,63 = 5 \cdot 10 +1 + 6 \cdot 10^{-1} +3 \cdot 10^{-2}$

$\text{B)} \ 249,99 = 2\cdot 10^2 + 4 \cdot 10 +9 + 9 \cdot 10^{-1} +9 \cdot 10^{-2}$

$\text{C)} \ \begin{aligned} 0,82694 & = 0 + 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\\[2ex] & = 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\end{aligned}$

$\text{D)} \ \begin{aligned} 5,7201 & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+0\cdot 10^{-3}+1\cdot 10^{-4}\\[2ex] & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+1\cdot 10^{-4} \end{aligned}$

تحليل متعدد الحدود (أو التعبير) لعدد

ما هو التحلل متعدد الحدود لعدد؟

كيفية القيام بتحليل كثير الحدود

أمثلة على التحلل متعدد الحدود للأرقام

تحليل متعدد الحدود للأعداد العشرية

حل تمارين تحليل كثيرات الحدود

التمرين 1

تمرين 2

التمرين 3

اترك تعليقاً إلغاء الرد